Lovász conjecture
Encyclopedia
In graph theory
, the Lovász conjecture (1970) is a classical problem on Hamiltonian path
s in graphs. It says:
The original article of Lovász
stated the result in the opposite, but
this version became standard. In 1996 Babai
published a conjecture sharply contradicting this conjecture, but both conjectures remain widely open.
It is not even known if a single counterexample would necessarily lead to a series of counterexamples.
As Knuth
describes it in volume 4 of The Art of Computer Programming
, the problem originated in British
campanology
(bell-ringing). Such Hamiltonian paths and cycles are also closely connected to Gray code
s. In each case the constructions are explicit.
There exists 5 examples of vertex-transitive graph with no Hamiltonian cycles (but with Hamiltonian paths) : the complete graph
K2, the Petersen graph
, the Coxeter graph
and two graphs derived from the Petersen and Coxeter graphs by replacing each vertex with a triangle.
The advantage of the Cayley graph formulation is that such graphs correspond to a finite group
and a
generating set
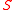. Thus one can ask for which 
and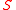 
the conjecture holds rather than attack it in full generality.
has a Hamiltonian path; however, every cyclic group whose order is not a prime power has a directed Cayley graph that does not have a Hamiltonian cycle.
In 1986, D. Witte proved that the Lovász conjecture holds for the Cayley graphs of p-group
s. It is open even for dihedral group
s, although for special sets of generators some progress has been made.
When group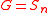
is a symmetric group
, there are many attractive generating sets. For example, the Lovász conjecture holds in the following cases of generating sets:
Stong has shown that the conjecture holds for the Cayley graph of the wreath product
Zm wr Zn with the natural minimal generating set when m is either even or three. In particular this holds for the cube-connected cycles
, which can be generated as the Cayley graph of the wreath product Z2 wr Zn.
Finally, it is known that for every finite group
there exists a generating set of size at most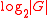 
such that the corresponding Cayley graph is Hamiltonian (Pak-Radoičić). This result is based on classification of finite simple groups
.
The Lovász conjecture was also established for random generating sets of size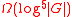
.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Lovász conjecture (1970) is a classical problem on Hamiltonian path
Hamiltonian path
In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle in an undirected graph that visits each vertex exactly once and also returns to the starting vertex...
s in graphs. It says:
- Every finite connected vertex-transitive graphVertex-transitive graphIn the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
contains a Hamiltonian path.
The original article of Lovász
László Lovász
László Lovász is a Hungarian mathematician, best known for his work in combinatorics, for which he was awarded the Wolf Prize and the Knuth Prize in 1999, and the Kyoto Prize in 2010....
stated the result in the opposite, but
this version became standard. In 1996 Babai
László Babai
László Babai is a Hungarian professor of mathematics and computer science at the University of Chicago. His research focuses on computational complexity theory, algorithms, combinatorics, and finite groups, with an emphasis on the interactions between these fields...
published a conjecture sharply contradicting this conjecture, but both conjectures remain widely open.
It is not even known if a single counterexample would necessarily lead to a series of counterexamples.
Historical remarks
The problem of finding Hamiltonian paths in highly symmetric graphs is quite old.As Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
describes it in volume 4 of The Art of Computer Programming
The Art of Computer Programming
The Art of Computer Programming is a comprehensive monograph written by Donald Knuth that covers many kinds of programming algorithms and their analysis....
, the problem originated in British
United Kingdom
The United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
campanology
Change ringing
Change ringing is the art of ringing a set of tuned bells in a series of mathematical patterns called "changes". It differs from many other forms of campanology in that no attempt is made to produce a conventional melody....
(bell-ringing). Such Hamiltonian paths and cycles are also closely connected to Gray code
Gray code
The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only one bit. It is a non-weighted code....
s. In each case the constructions are explicit.
Hamiltonian cycle
Another version of Lovász conjecture states that- Every finite connected vertex-transitive graphVertex-transitive graphIn the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
contains a Hamiltonian cycle except the five known counterexamples.
There exists 5 examples of vertex-transitive graph with no Hamiltonian cycles (but with Hamiltonian paths) : the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
K2, the Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
, the Coxeter graph
Coxeter graph
In the mathematical field of graph theory, the Coxeter graph is a 3-regular graph with 28 vertices and 42 edges. All the cubic distance-regular graphs are known. The Coxeter graph is one of the 13 such graphs....
and two graphs derived from the Petersen and Coxeter graphs by replacing each vertex with a triangle.
Cayley graphs
None of the 5 vertex-transitive graphs with no Hamiltonian cycles is a Cayley graph, therefore that leads to a weaker version of the conjecture :- Every finite connected Cayley graphCayley graphIn mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
contains a Hamiltonian cycle.
The advantage of the Cayley graph formulation is that such graphs correspond to a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
and agenerating set
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
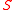. Thus one can ask for which and 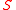the conjecture holds rather than attack it in full generality.Directed Cayley graph
For directed Cayley graphs (digraphs) the Lovász conjecture is false. Various counterexamples were obtained by R.A. Rankin. Still, many of the below results hold in this restrictive setting.Special cases
Every directed Cayley graph of an abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
has a Hamiltonian path; however, every cyclic group whose order is not a prime power has a directed Cayley graph that does not have a Hamiltonian cycle.
In 1986, D. Witte proved that the Lovász conjecture holds for the Cayley graphs of p-group
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
s. It is open even for dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
s, although for special sets of generators some progress has been made.
When group
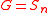is a symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
, there are many attractive generating sets. For example, the Lovász conjecture holds in the following cases of generating sets:
-
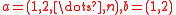(long cycle and a transposition). -
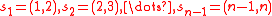(Coxeter generatorsCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
). In this case a Hamiltonian cycle is generated by the Steinhaus–Johnson–Trotter algorithm. - any set of transpositions corresponding to a labelled treeTree (graph theory)In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
on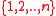
. -
Stong has shown that the conjecture holds for the Cayley graph of the wreath product
Wreath product
In mathematics, the wreath product of group theory is a specialized product of two groups, based on a semidirect product. Wreath products are an important tool in the classification of permutation groups and also provide a way of constructing interesting examples of groups.Given two groups A and H...
Zm wr Zn with the natural minimal generating set when m is either even or three. In particular this holds for the cube-connected cycles
Cube-connected cycles
In graph theory, the cube-connected cycles is an undirected cubic graph, formed by replacing each vertex of a hypercube graph by a cycle. It was introduced by for use as a network topology in parallel computing.- Definition :...
, which can be generated as the Cayley graph of the wreath product Z2 wr Zn.
General groups
For general finite groups, only a few results are known:-
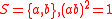(R.A. Rankin generators) -
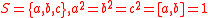(Rapaport-Strasser generators) -
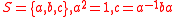(PakIgor PakIgor Pak is a professor of mathematics at the University of California, Los Angeles, working in combinatorics and discrete probability...
-Radoičić generators) -
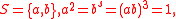where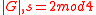 
(here we have (2,s,3)-presentationPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
, Glover-Marušič theorem).
Finally, it is known that for every finite group
there exists a generating set of size at most 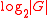such that the corresponding Cayley graph is Hamiltonian (Pak-Radoičić). This result is based on classification of finite simple groupsClassification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
.
The Lovász conjecture was also established for random generating sets of size
.
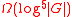