
Loop algebra
Encyclopedia
In mathematics
, loop algebras are certain types of Lie algebra
, of particular interest in theoretical physics
.
If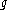 is a Lie algebra, the tensor product
is a Lie algebra, the tensor product
of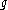 with
with  ,
,
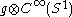 ,
,
the algebra
of (complex) smooth function
s over the circle manifold
S1 is an infinite-dimensional Lie algebra with the Lie bracket
given by
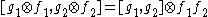 .
.
Here g1 and g2 are elements of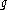 and f1 and f2 are elements of
and f1 and f2 are elements of 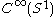 .
.
This isn't precisely what would correspond to the direct product
of infinitely many copies of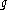 , one for each point in S1, because of the smoothness restriction. Instead, it can be thought of in terms of smooth map from S1 to
, one for each point in S1, because of the smoothness restriction. Instead, it can be thought of in terms of smooth map from S1 to 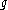 ; a smooth parameterized loop in
; a smooth parameterized loop in  , in other words. This is why it is called the loop algebra.
, in other words. This is why it is called the loop algebra.
We can take the Fourier transform
on this loop algebra by defining
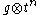
as
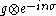
where
is a coordinatization of S1.
If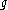 is a semisimple Lie algebra, then a nontrivial central extension of its loop algebra gives rise to an affine Kac-Moody algebra.
is a semisimple Lie algebra, then a nontrivial central extension of its loop algebra gives rise to an affine Kac-Moody algebra.
Similarly, a set of all smooth maps from S1 to a Lie group
G forms an infinite-dimensional Lie group (Lie group in the sense we can define functional derivative
s over it) called the loop group
. The Lie algebra of a loop group is the corresponding loop algebra.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, loop algebras are certain types of Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, of particular interest in theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
.
If
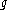 is a Lie algebra, the tensor product
is a Lie algebra, the tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of
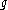 with
with  ,
,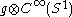 ,
,the algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
of (complex) smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s over the circle manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
S1 is an infinite-dimensional Lie algebra with the Lie bracket
Lie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
given by
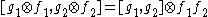 .
.Here g1 and g2 are elements of
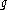 and f1 and f2 are elements of
and f1 and f2 are elements of 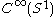 .
.This isn't precisely what would correspond to the direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
of infinitely many copies of
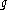 , one for each point in S1, because of the smoothness restriction. Instead, it can be thought of in terms of smooth map from S1 to
, one for each point in S1, because of the smoothness restriction. Instead, it can be thought of in terms of smooth map from S1 to 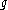 ; a smooth parameterized loop in
; a smooth parameterized loop in  , in other words. This is why it is called the loop algebra.
, in other words. This is why it is called the loop algebra.We can take the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
on this loop algebra by defining
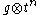
as
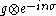
where
- 0 ≤ σ <2π
is a coordinatization of S1.
If
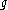 is a semisimple Lie algebra, then a nontrivial central extension of its loop algebra gives rise to an affine Kac-Moody algebra.
is a semisimple Lie algebra, then a nontrivial central extension of its loop algebra gives rise to an affine Kac-Moody algebra.Similarly, a set of all smooth maps from S1 to a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G forms an infinite-dimensional Lie group (Lie group in the sense we can define functional derivative
Functional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
s over it) called the loop group
Loop group
In mathematics, a loop group is a group of loops in a topological group G with multiplication defined pointwise. Specifically, letLG \,denote the space of continuous mapsS^1 \to G...
. The Lie algebra of a loop group is the corresponding loop algebra.

