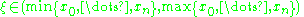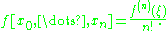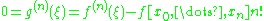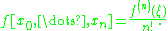Mean value theorem (divided differences)
Encyclopedia
In mathematical analysis
, the mean value theorem for divided differences generalizes the mean value theorem
to higher derivatives.
where the nth derivative of f equals n! times the nth divided difference at these points:
For n = 1, that is two function points, one obtains the simple mean value theorem
.
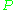be the Lagrange interpolation polynomial for f at x0, ..., xn.
Then it follows from the Newton form
of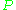
that the highest term of 
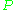is 
.
Let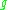
be the remainder of the interpolation, defined by 
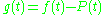. Then 
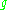has 
zeros: x0, ..., xn.
By applying Rolle's theorem
first to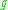
, then to 
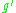, and so on until 
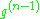, we find that 
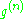has a zero 
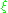. This means that
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, the mean value theorem for divided differences generalizes the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
to higher derivatives.
Statement of the theorem
For any n + 1 pairwise distinct points x0, ..., xn in the domain of an n-times differentiable function f there exists an interior point
where the nth derivative of f equals n
For n = 1, that is two function points, one obtains the simple mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
.
Proof
Let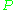 be the Lagrange interpolation polynomial for f at x0, ..., xn.Then it follows from the Newton form
Newton polynomial
In the mathematical field of numerical analysis, a Newton polynomial, named after its inventor Isaac Newton, is the interpolation polynomial for a given set of data points in the Newton form...
of
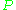that the highest term of 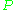is .Let
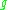be the remainder of the interpolation, defined by 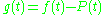. Then 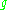has zeros: x0, ..., xn.By applying Rolle's theorem
Rolle's theorem
In calculus, Rolle's theorem essentially states that a differentiable function which attains equal values at two distinct points must have a point somewhere between them where the first derivative is zero.-Standard version of the theorem:If a real-valued function ƒ is continuous on a closed...
first to
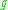, then to 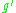, and so on until 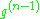, we find that 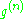has a zero 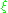. This means that
