Lie bialgebra
Encyclopedia
In mathematics
, a Lie bialgebra is the Lie-theoretic case of a bialgebra
: its a set with a Lie algebra
and a Lie coalgebra
structure which are compatible.
It is a bialgebra
where the comultiplication is skew-symmetric and satisfies a dual Jacobi identity
, so that the dual vector space is a Lie algebra
, whereas the comultiplication is a 1-cocycle
, so that the multiplication and comultiplication are compatible. The cocycle condition implies that, in practice, one studies only classes of bialgebras that are cohomologous to a Lie bialgebra on a coboundary.
They are also called Poisson-Hopf algebras, and are the Lie algebra
of a Poisson-Lie group
.
Lie bialgebras occur naturally in the study of the Yang-Baxter equation
s.
, is called the cocommutator, and must satisfy two properties. The dual
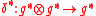
must be a Lie bracket on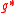
, and it must be a cocycle:
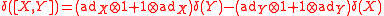
where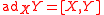
is the adjoint.
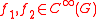being two smooth functions on the group manifold. Let 
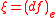be the differential at the identity element. Clearly, 
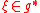. The Poisson structure on the group then induces a bracket on 
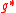, as
where
is the Poisson bracket
. Given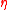
be the Poisson bivector on the manifold, define 
to be the right-translate of the bivector to the identity element in G. Then one has that
The cocommutator is then the tangent map:
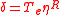
so that
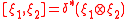
is the dual of the cocommutator.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Lie bialgebra is the Lie-theoretic case of a bialgebra
Bialgebra
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....
: its a set with a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
and a Lie coalgebra
Lie coalgebra
In mathematics a Lie coalgebra is the dual structure to a Lie algebra.In finite dimensions, these are dual objects: the dual vector space to a Lie algebra naturally has the structure of a Lie coalgebra, and conversely.-Definition:...
structure which are compatible.
It is a bialgebra
Bialgebra
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....
where the comultiplication is skew-symmetric and satisfies a dual Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
, so that the dual vector space is a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, whereas the comultiplication is a 1-cocycle
Cocycle
A cocycle refers to any one of the following:*A closed cochain in algebraic topology is called a cocycle.*A particular type of map in an autonomous dynamical system; see Oseledec theorem....
, so that the multiplication and comultiplication are compatible. The cocycle condition implies that, in practice, one studies only classes of bialgebras that are cohomologous to a Lie bialgebra on a coboundary.
They are also called Poisson-Hopf algebras, and are the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of a Poisson-Lie group
Poisson-Lie group
In mathematics, a Poisson–Lie group is a Poisson manifold that is also a Lie group, with the group multiplication being compatible with the Poisson algebra structure on the manifold...
.
Lie bialgebras occur naturally in the study of the Yang-Baxter equation
Yang-Baxter equation
The Yang–Baxter equation is an equation which was first introduced in the field of statistical mechanics. It takes its name from independent work of C. N. Yang from 1968, and R. J. Baxter from 1971...
s.
Definition
More precisely, comultiplication on the algebra,, is called the cocommutator, and must satisfy two properties. The dual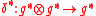must be a Lie bracket on
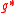, and it must be a cocycle: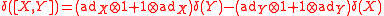where
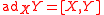is the adjoint.Relation to Poisson-Lie groups
Let G be a Poisson-Lie group, with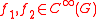 being two smooth functions on the group manifold. Let 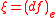be the differential at the identity element. Clearly, 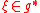. The Poisson structure on the group then induces a bracket on 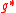, aswhere
is the Poisson bracketPoisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
. Given
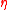be the Poisson bivector on the manifold, define to be the right-translate of the bivector to the identity element in G. Then one has thatThe cocommutator is then the tangent map:
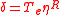
so that
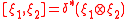
is the dual of the cocommutator.