Lie coalgebra
Encyclopedia
In mathematics
a Lie coalgebra is the dual structure to a Lie algebra
.
In finite dimensions, these are dual objects: the dual vector space to a Lie algebra
naturally has the structure of a Lie coalgebra, and conversely.
over a field
k equipped with a linear mapping
from E to the exterior product of E with itself. It is possible to extend d uniquely to a graded derivation of degree 1 on the exterior algebra
of E: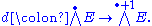
Then the pair (E, d) is said to be a Lie coalgebra if d2 = 0,
i.e., if the graded components of the exterior algebra
with derivation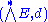
form a cochain complex: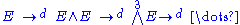
s on a manifold form a Lie algebra (over the base field K), the de Rham complex of differential forms on a manifold form a Lie coalgebra (over the base field K). Further, there is a pairing between vector fields and differential forms.
However, the situation is subtler: the Lie bracket is not linear over the algebra of smooth functions
(the error is the Lie derivative
), nor is the exterior derivative
:
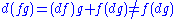(it is a derivation, not linear over functions): they are not tensor
s. They are not linear over functions, but they behave in a consistent way, which is not captured simply by the notion of Lie algebra and Lie coalgebra.
Further, in the de Rham complex, the derivation is not only defined for
, but is also defined for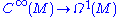 
.
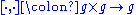which is skew-symmetric, and satisfies the Jacobi identity. Equivalently, a map 
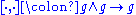that satisfies the Jacobi identity
.
Dually, a Lie coalgebra structure on a vector space is a map
which satisfies the cocycle
condition. The dual of the Lie bracket yields a map (the cocommutator)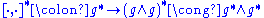
where the isomorphism
holds in finite dimension; dually for the dual of Lie comultiplication. In this context, the Jacobi identity corresponds to the cocycle
condition.
More explicitly, let E be a Lie coalgebra over a field of characteristic neither 2 nor 3. The dual space E* carries the structure of a bracket defined by
We show that this endows E* with a Lie bracket. It suffices to check the Jacobi identity
. For any x, y, z ∈ E* and α ∈ E,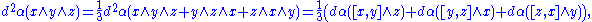
where the latter step follows from the standard identification of the dual of a wedge product with the wedge product of the duals. Finally, this gives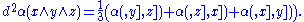
Since d2 = 0, it follows that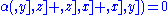
, for any α, x, y, and z.
Thus, by the double-duality isomorphism (more precisely, by the double-duality monomorphism, since the vector space needs not be finite-dimensional), the Jacobi identity is satisfied.
In particular, note that this proof demonstrates that the cocycle
condition d2 = 0 is in a sense dual to the Jacobi identity.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
a Lie coalgebra is the dual structure to a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
.
In finite dimensions, these are dual objects: the dual vector space to a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
naturally has the structure of a Lie coalgebra, and conversely.
Definition
Let E be a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k equipped with a linear mapping
from E to the exterior product of E with itself. It is possible to extend d uniquely to a graded derivation of degree 1 on the exterior algebraExterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
of E:
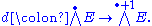
Then the pair (E, d) is said to be a Lie coalgebra if d2 = 0,
i.e., if the graded components of the exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
with derivation
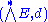
form a cochain complex:
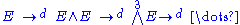
Relation to de Rham complex
Just as the exterior algebra (and tensor algebra) of vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s on a manifold form a Lie algebra (over the base field K), the de Rham complex of differential forms on a manifold form a Lie coalgebra (over the base field K). Further, there is a pairing between vector fields and differential forms.
However, the situation is subtler: the Lie bracket is not linear over the algebra of smooth functions
(the error is the Lie derivativeLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
), nor is the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
:
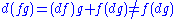(it is a derivation, not linear over functions): they are not tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s. They are not linear over functions, but they behave in a consistent way, which is not captured simply by the notion of Lie algebra and Lie coalgebra.
Further, in the de Rham complex, the derivation is not only defined for
, but is also defined for 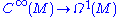.The Lie algebra on the dual
A Lie algebra structure on a vector space is a map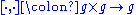 which is skew-symmetric, and satisfies the Jacobi identity. Equivalently, a map 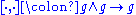that satisfies the Jacobi identityJacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
.
Dually, a Lie coalgebra structure on a vector space is a map
which satisfies the cocycleCocycle
A cocycle refers to any one of the following:*A closed cochain in algebraic topology is called a cocycle.*A particular type of map in an autonomous dynamical system; see Oseledec theorem....
condition. The dual of the Lie bracket yields a map (the cocommutator)
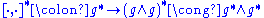
where the isomorphism
holds in finite dimension; dually for the dual of Lie comultiplication. In this context, the Jacobi identity corresponds to the cocycleCocycle
A cocycle refers to any one of the following:*A closed cochain in algebraic topology is called a cocycle.*A particular type of map in an autonomous dynamical system; see Oseledec theorem....
condition.
More explicitly, let E be a Lie coalgebra over a field of characteristic neither 2 nor 3. The dual space E* carries the structure of a bracket defined by
- α([x, y]) = dα(x∧y), for all α ∈ E and x,y ∈ E*.
We show that this endows E* with a Lie bracket. It suffices to check the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
. For any x, y, z ∈ E* and α ∈ E,
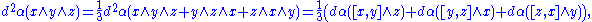
where the latter step follows from the standard identification of the dual of a wedge product with the wedge product of the duals. Finally, this gives
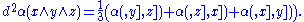
Since d2 = 0, it follows that
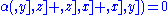, for any α, x, y, and z.Thus, by the double-duality isomorphism (more precisely, by the double-duality monomorphism, since the vector space needs not be finite-dimensional), the Jacobi identity is satisfied.
In particular, note that this proof demonstrates that the cocycle
Cocycle
A cocycle refers to any one of the following:*A closed cochain in algebraic topology is called a cocycle.*A particular type of map in an autonomous dynamical system; see Oseledec theorem....
condition d2 = 0 is in a sense dual to the Jacobi identity.