
Lebesgue's decomposition theorem
Encyclopedia
In mathematics
, more precisely in measure theory, Lebesgue's decomposition theorem is a theorem
which states that given and
and  two σ-finite
two σ-finite
signed measure
s on a measurable space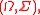 there exist two σ-finite signed measures
there exist two σ-finite signed measures 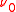 and
and 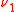 such that:
such that:
These two measures are uniquely determined.
First, the decomposition of the singular
part can refined:
where
Second, absolutely continuous measures are classified by the Radon–Nikodym theorem
, and discrete measures are easily understood. Hence (singular continuous measures aside), Lebesgue decomposition gives a very explicit description of measures. The Cantor measure (the probability measure
on the real line
whose cumulative distribution function
is the Cantor function
) is an example of a singular continuous measure.
X, it can be decomposed as a sum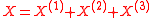 where:
where:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more precisely in measure theory, Lebesgue's decomposition theorem is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
which states that given
 and
and  two σ-finite
two σ-finiteSigma-finite measure
In mathematics, a positive measure μ defined on a σ-algebra Σ of subsets of a set X is called finite if μ is a finite real number . The measure μ is called σ-finite if X is the countable union of measurable sets of finite measure...
signed measure
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
s on a measurable space
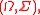 there exist two σ-finite signed measures
there exist two σ-finite signed measures 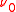 and
and 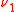 such that:
such that:-

-
 (that is,
(that is, 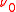 is absolutely continuous with respect to
is absolutely continuous with respect to  )
) -
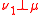 (that is,
(that is, 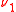 and
and  are singularSingular measureIn mathematics, two positive measures μ and ν defined on a measurable space are called singular if there exist two disjoint sets A and B in Σ whose union is Ω such that μ is zero on all measurable subsets of B while ν is zero on all measurable subsets of A...
are singularSingular measureIn mathematics, two positive measures μ and ν defined on a measurable space are called singular if there exist two disjoint sets A and B in Σ whose union is Ω such that μ is zero on all measurable subsets of B while ν is zero on all measurable subsets of A...
).
These two measures are uniquely determined.
Refinement
Lebesgue's decomposition theorem can be refined in a number of ways.First, the decomposition of the singular
Singular measure
In mathematics, two positive measures μ and ν defined on a measurable space are called singular if there exist two disjoint sets A and B in Σ whose union is Ω such that μ is zero on all measurable subsets of B while ν is zero on all measurable subsets of A...
part can refined:

where
- νcont is the absolutely continuous part
- νsing is the singular continuous part
- νpp is the pure point part (a discrete measureDiscrete measureIn mathematics, more precisely in measure theory, a measure on the real line is called a discrete measure if its support is at most a countable set. Note that the support need not be a discrete set...
).
Second, absolutely continuous measures are classified by the Radon–Nikodym theorem
Radon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
, and discrete measures are easily understood. Hence (singular continuous measures aside), Lebesgue decomposition gives a very explicit description of measures. The Cantor measure (the probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
whose cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
is the Cantor function
Cantor function
In mathematics, the Cantor function, named after Georg Cantor, is an example of a function that is continuous, but not absolutely continuous. It is also referred to as the Devil's staircase.-Definition:See figure...
) is an example of a singular continuous measure.
Lévy–Itō decomposition
The analogous decomposition for a stochastic processes is the Lévy–Itō decomposition: given a Lévy processLévy process
In probability theory, a Lévy process, named after the French mathematician Paul Lévy, is any continuous-time stochastic process that starts at 0, admits càdlàg modification and has "stationary independent increments" — this phrase will be explained below...
X, it can be decomposed as a sum
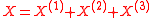 where:
where:
-
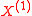 is a Brownian motionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
is a Brownian motionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
with drift, corresponding to the absolutely continuous part; -
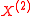 is a compound Poisson processCompound Poisson processA compound Poisson process is a continuous-time stochastic process with jumps. The jumps arrive randomly according to a Poisson process and the size of the jumps is also random, with a specified probability distribution...
is a compound Poisson processCompound Poisson processA compound Poisson process is a continuous-time stochastic process with jumps. The jumps arrive randomly according to a Poisson process and the size of the jumps is also random, with a specified probability distribution...
, corresponding to the pure point part; -
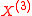 is a square integrable pure jump martingaleMartingale (probability theory)In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
is a square integrable pure jump martingaleMartingale (probability theory)In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
that almost surely has a countable number of jumps on a finite interval, corresponding to the singular continuous part.
See also
- Decomposition of spectrumDecomposition of spectrum (functional analysis)In mathematics, especially functional analysis, the spectrum of an operator generalizes the notion of eigenvalues. Given an operator, it is sometimes useful to break up the spectrum into various parts...

