In mathematics, the goal of lattice basis reduction is given an integer lattice

Lattice (group)

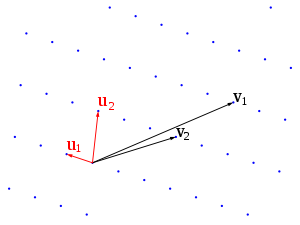
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...

 basis as input, to find a basis

Basis (linear algebra)

In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...

 with short, nearly orthogonal vectors. This is realized using different algorithms, whose running time is usually at least exponential in the dimension of the lattice.

Nearly Orthogonal

One measure of nearly orthogonal is the orthogonality defect. This compares the product of the lengths of the basis vectors with the volume of the parallelepiped

Parallelepiped

In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...

 they define. For perfectly orthogonal basis vectors, these quantities would be the same.

Any particular basis of vectors may be represented by a matrix

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

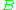 , whose columns are the basis vectors 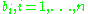. In the fully dimensional case where the number of basis vectors is equal to the dimension of the space they occupy, this matrix is square, and the volume of the fundamental parallelepiped is simply the absolute value of the determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

 of this matrix 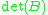. If the number of vectors is less than the dimension of the underlying space, then volume is 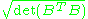. For a given lattice 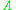, this volume is the same (up to sign) for any basis, and hence is referred to as the determinant of the lattice 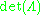or lattice constant .

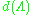The orthogonality defect is the product of the basis vector lengths divided by the parallelepiped volume;


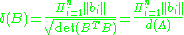
From the geometric definition it may be appreciated that 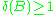with equality if and only if the basis is orthogonal.

If the lattice reduction problem is defined as finding the basis with the smallest possible defect, then the problem is NP complete. However, there exist polynomial time algorithms to find a basis with defect
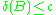
where c is some constant depending only on the number of basis vectors and the dimension of the underlying space (if different). This is a good enough solution in many practical applications.

In two dimensions

For a basis consisting of just two vectors, there is a simple and efficient method of reduction closely analogous to the Euclidean algorithm

Euclidean algorithm

In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...

 for the greatest common divisor

Greatest common divisor

In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...

 of two integers. As with the Euclidean algorithm, the method is iterative; at each step the larger of the two vectors is reduced by adding or subtracting an integer multiple of the smaller vector.

Applications

Lattice reduction algorithms are used in a number of modern number theoretical applications, including in the discovery of a spigot algorithm

Spigot algorithm

A spigot algorithm is a type of algorithm used to compute the value of a mathematical constant such as π or e. Unlike recursive algorithms, a spigot algorithm yields digits incrementally without using previously computed digits...

  for pi. Although determining the shortest basis is possibly an NP-complete problem, algorithms such as the LLL algorithm

Lenstra–Lenstra–Lovász lattice basis reduction algorithm

The LLL-reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik Lenstra and László Lovász in 1982, see...

  can find a short basis in polynomial time with guaranteed worst-case performance. LLL

Lenstra–Lenstra–Lovász lattice basis reduction algorithm

The LLL-reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik Lenstra and László Lovász in 1982, see...

 is widely used in the cryptanalysis

Cryptanalysis

Cryptanalysis is the study of methods for obtaining the meaning of encrypted information, without access to the secret information that is normally required to do so. Typically, this involves knowing how the system works and finding a secret key...

 of public key

Public-key cryptography

Public-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...

 cryptosystems.

When used to find integer relations, a typical input to the algorithm consists of an augmented nxn identity matrix with the entries in the last column consisting of the n elements (multiplied by a large positive constant w to penalize vectors that do not sum to zero) between which the relation is sought.

The LLL algorithm for computing a nearly-orthogonal basis was used to show that integer programming

Integer programming

An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming, which is also known as mixed integer programming.Integer programming is NP-hard...

 in any fixed dimension can be done in polynomial time

P (complexity)

In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...

.

Algorithms

The following algorithms reduce lattice bases. They can be compared in terms of runtime and approximation to an optimal solution, always relative to the dimension of the given lattice. If there are public implementations of these algorithms this should also be noted here.

Year	Algorithm	Name	Implementation
1982	LLL Lenstra–Lenstra–Lovász lattice basis reduction algorithm The LLL-reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik Lenstra and László Lovász in 1982, see...	Lenstra Lenstra Lovász	NTL Number Theory Library NTL is a C++ library for doing number theory. NTL supports arbitrary length integer and arbitrary precision floating point arithmetic, finite fields, vectors, matrices, polynomials, lattice basis reduction and basic linear algebra. NTL is free software released under the GNU General Public License....
1987	BKZ	Block Korkine Zolotarev	NTL Number Theory Library NTL is a C++ library for doing number theory. NTL supports arbitrary length integer and arbitrary precision floating point arithmetic, finite fields, vectors, matrices, polynomials, lattice basis reduction and basic linear algebra. NTL is free software released under the GNU General Public License....
2002	RSR	Random Sampling Reduction
2002	PDR	Primal Dual Reduction