
Lagrange's theorem (group theory)
Encyclopedia
Lagrange's theorem, in the mathematics
of group theory
, states that for any finite group
G, the order
(number of elements) of every subgroup
H of G divides the order of G. The theorem is named after Joseph Lagrange
.
s of H in G. The left cosets are the equivalence classes of a certain equivalence relation
on G and therefore form a partition
of G. Specifically, x and y in G are related if and only if there exists h in H such that x = yh. If we can show that all cosets of H have the same number of elements, then each coset of H has precisely |H| elements. We are then done since the order of H times the number of cosets is equal to the number of elements in G, thereby proving that the order of H divides the order of G. Now, if aH and bH are two left cosets of H, we can define a map f : aH → bH by setting f(x) = ba-1x. This map is bijective because its inverse is given by
This proof also shows that the quotient of the orders |G| / |H| is equal to the index
[G : H] (the number of left cosets of H in G). If we write this statement as
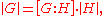
then, seen as a statement about cardinal number
s, it is equivalent to the Axiom of choice.
a of a finite group (i.e. the smallest positive integer number k with ak = e, where e is the identity element of the group) divides the order of that group, since the order of a is equal to the order of the cyclic
subgroup generated
by a. If the group has n elements, it follows

This can be used to prove Fermat's little theorem
and its generalization, Euler's theorem. These special cases were known long before the general theorem was proved.
The theorem also shows that any group of prime order is cyclic and simple
. This in turn can be used to prove Wilson's theorem, that if p is prime then p is a factor of (p-1)!+1.
and that every supersolvable group
is a CLT group: however there exists solvable groups which are not CLT and CLT groups which are not supersolvable.
There are partial converses to Lagrange's theorem. For general groups, Cauchy's theorem
guarantees the existence of an element, and hence of a cyclic subgroup, of order any prime dividing the group order; Sylow's theorem extends this to the existence of a subgroup of order equal to the maximal power of any prime dividing the group order. For solvable groups, Hall's theorems assert the existence of a subgroup of order equal to any unitary divisor of the group order (that is, a divisor coprime to its cofactor).
Lagrange did not prove his theorem; all he did, essentially, was to discuss some special cases. The first complete proof of the theorem was provided by Abbati
and published in 1803.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, states that for any finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
G, the order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
(number of elements) of every subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
H of G divides the order of G. The theorem is named after Joseph Lagrange
Joseph Lagrange
Count Joseph Lagrange was a French soldier who rose through the ranks and gained promotion to the rank of general officer during the French Revolutionary Wars, subsequently pursuing a successful career during the Napoleonic Wars and winning promotion to the top military rank of General of Division....
.
Proof of Lagrange's Theorem
This can be shown using the concept of left cosetCoset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s of H in G. The left cosets are the equivalence classes of a certain equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on G and therefore form a partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of G. Specifically, x and y in G are related if and only if there exists h in H such that x = yh. If we can show that all cosets of H have the same number of elements, then each coset of H has precisely |H| elements. We are then done since the order of H times the number of cosets is equal to the number of elements in G, thereby proving that the order of H divides the order of G. Now, if aH and bH are two left cosets of H, we can define a map f : aH → bH by setting f(x) = ba-1x. This map is bijective because its inverse is given by

This proof also shows that the quotient of the orders |G| / |H| is equal to the index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
[G : H] (the number of left cosets of H in G). If we write this statement as
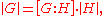
then, seen as a statement about cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s, it is equivalent to the Axiom of choice.
Using the theorem
A consequence of the theorem is that the order of any elementOrder (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
a of a finite group (i.e. the smallest positive integer number k with ak = e, where e is the identity element of the group) divides the order of that group, since the order of a is equal to the order of the cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
subgroup generated
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
by a. If the group has n elements, it follows

This can be used to prove Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
and its generalization, Euler's theorem. These special cases were known long before the general theorem was proved.
The theorem also shows that any group of prime order is cyclic and simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
. This in turn can be used to prove Wilson's theorem, that if p is prime then p is a factor of (p-1)!+1.
Existence of subgroups of given order
Lagrange's theorem raises the converse question as to whether every divisor of the order of a group is the order of some subgroup. This does not hold in general: given a finite group G and a divisor d of |G|, there does not necessarily exist a subgroup of G with order d. The smallest example is the alternating group G = A4 which has 12 elements but no subgroup of order 6. A CLT group is a finite group with the property that for every divisor of the order of the group, there is a subgroup of that order. It is known that a CLT group must be solvableSolvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
and that every supersolvable group
Supersolvable group
In mathematics, a group is supersolvable if it has an invariant normal series where all the factors are cyclic groups. Supersolvability is stronger than the notion of solvability.-Definition:Let G be a group...
is a CLT group: however there exists solvable groups which are not CLT and CLT groups which are not supersolvable.
There are partial converses to Lagrange's theorem. For general groups, Cauchy's theorem
Cauchy's theorem (group theory)
Cauchy's theorem is a theorem in the mathematics of group theory, named after Augustin Louis Cauchy. It states that if G is a finite group and p is a prime number dividing the order of G , then G contains an element of order p...
guarantees the existence of an element, and hence of a cyclic subgroup, of order any prime dividing the group order; Sylow's theorem extends this to the existence of a subgroup of order equal to the maximal power of any prime dividing the group order. For solvable groups, Hall's theorems assert the existence of a subgroup of order equal to any unitary divisor of the group order (that is, a divisor coprime to its cofactor).
History
Lagrange did not prove Lagrange's theorem in its general form. He stated, in his article Réflexions sur la résolution algébrique des équations, that if a polynomial in n variables has its variables permuted in all n ! ways, the number of different polynomials that are obtained is always a factor of n !. (For example if the variables x, y, and z are permuted in all 6 possible ways in the polynomial x + y - z then we get a total of 3 different polynomials: x + y − z, x + z - y, and y + z − x. Note that 3 is a factor of 6.) The number of such polynomials is the index in the symmetric group Sn of the subgroup H of permutations which preserve the polynomial. (For the example of x + y − z, the subgroup H in S3 contains the identity and the transposition (xy).) So the size of H divides n !. With the later development of abstract groups, this result of Lagrange on polynomials was recognized to extend to the general theorem about finite groups which now bears his name.Lagrange did not prove his theorem; all he did, essentially, was to discuss some special cases. The first complete proof of the theorem was provided by Abbati
Pietro Abbati Marescotti
Pietro Abbati Marescotti was an Italian mathematician who taught in Modena.Pietro Abbati was descended from the 16th century noble family of Abbati, who were related to the Marescotti family of Modena...
and published in 1803.

