
Lagrange's identity
Encyclopedia
In algebra
, Lagrange's identity, named after Joseph Louis Lagrange
, is:
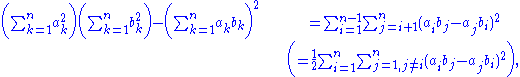
which applies to any two sets {a1, a2, . . ., an} and {b1, b2, . . ., bn} of real
or complex number
s (or more generally, elements of a commutative ring
). This identity is a special form of the Binet–Cauchy identity.
In a more compact vector notation, Lagrange's identity is expressed as:
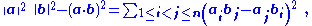
where a and b are n-dimensional vectors with components that are real numbers. The extension to complex numbers requires the interpretation of the dot product as an inner product or Hermitian dot product. Explicitly, for complex numbers, Lagrange's identity can be written in the form:
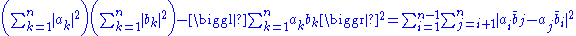
involving the absolute value.
Since the right-hand side of the identity is clearly non-negative, it implies Cauchy's inequality in the finite-dimensional
real coordinate space ℝn and its complex counterpart ℂn.
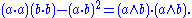
Hence, it can be seen as a formula which gives the length of the wedge product of two vectors, which is the area of the paralleogram they define, in terms of the dot products of the two vectors, as
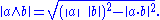
and dot product
:
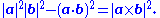
Using the definition of angle based upon the dot product (see also Cauchy–Schwarz inequality), the left-hand side is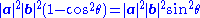
where θ is the angle formed by the vectors a and b. The area of a parallelogram with sides |a| and |b| and angle θ is known in elementary geometry to be
so the left-hand side of Lagrange's identity is the squared area of the parallelogram. The cross product appearing on the right-hand side is defined by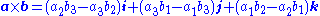
which is a vector whose components are equal in magnitude to the areas of the projections of the parallelogram onto the yz, zx, and xy planes, respectively.
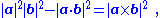
However, the cross product in 7 dimensions does not share all the properties of the cross product in 3 dimensions. For example, the direction of a × b in 7-dimensions may be the same as c × d even though c and d are linearly independent of a and b. Also the seven dimensional cross product
is not compatible with the Jacobi identity
.
p is defined as the sum of a scalar t and a vector v:

The product of two quaternions and is defined by
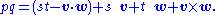
The quaternionic conjugate of q is defined by
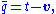
and the norm squared is
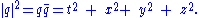
The multiplicativity of the norm in the quaternion algebra provides, for quaternions p and q:
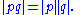
The quaternions p and q are called imaginary if their scalar part is zero; equivalently, if

Lagrange's identity is just the multiplicativity of the norm of imaginary quaternions,
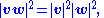
since, by definition,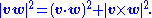
s of ai and bi, respectively,
Here is also a direct proof. The expansion of the first term on the left side is:
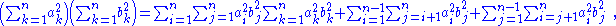
which means that the product of a column of as and a row of bs yields (a sum of elements of) a square of abs, which can be broken up into a diagonal and a pair of triangles on either side of the diagonal.
The second term on the left side of Lagrange's identity can be expanded as:
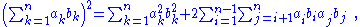
which means that a symmetric square can be broken up into its diagonal and a pair of equal triangles on either side of the diagonal.
To expand the summation on the right side of Lagrange's identity, first expand the square within the summation:
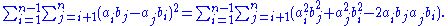
Distribute the summation on the right side,
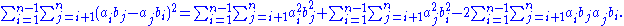
Now exchange the indices i and j of the second term on the right side, and permute the b factors of the third term, yielding:
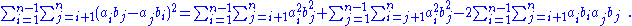
Back to the left side of Lagrange's identity: it has two terms, given in expanded form by Equations () and (). The first term on the right side of Equation () ends up canceling out the first term on the right side of Equation (), yielding
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, Lagrange's identity, named after Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
, is:
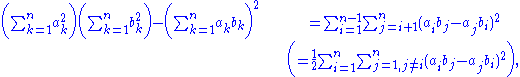
which applies to any two sets {a1, a2, . . ., an} and {b1, b2, . . ., bn} of real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s (or more generally, elements of a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
). This identity is a special form of the Binet–Cauchy identity.
In a more compact vector notation, Lagrange's identity is expressed as:
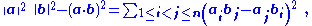
where a and b are n-dimensional vectors with components that are real numbers. The extension to complex numbers requires the interpretation of the dot product as an inner product or Hermitian dot product. Explicitly, for complex numbers, Lagrange's identity can be written in the form:
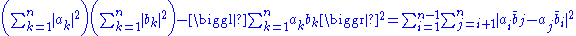
involving the absolute value.
Since the right-hand side of the identity is clearly non-negative, it implies Cauchy's inequality in the finite-dimensional
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
real coordinate space ℝn and its complex counterpart ℂn.
Lagrange's identity and exterior algebra
In terms of the wedge product, Lagrange's identity can be written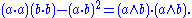
Hence, it can be seen as a formula which gives the length of the wedge product of two vectors, which is the area of the paralleogram they define, in terms of the dot products of the two vectors, as
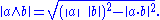
Lagrange's identity and vector calculus
In three dimensions, Lagrange's identity asserts that the square of the area of a parallelogram in space is equal to the sum of the squares of its projections onto the Cartesian coordinate planes. Algebraically, if a and b are vectors in ℝ3 with lengths |a| and |b|, then Lagrange's identity can be written in terms of the cross productCross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
and dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
:
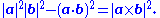
Using the definition of angle based upon the dot product (see also Cauchy–Schwarz inequality), the left-hand side is
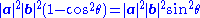
where θ is the angle formed by the vectors a and b. The area of a parallelogram with sides |a| and |b| and angle θ is known in elementary geometry to be

so the left-hand side of Lagrange's identity is the squared area of the parallelogram. The cross product appearing on the right-hand side is defined by
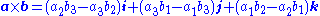
which is a vector whose components are equal in magnitude to the areas of the projections of the parallelogram onto the yz, zx, and xy planes, respectively.
Seven dimensions
For a and b as vectors in ℝ7, Lagrange's identity takes on the same form as in the case of ℝ3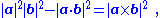
However, the cross product in 7 dimensions does not share all the properties of the cross product in 3 dimensions. For example, the direction of a × b in 7-dimensions may be the same as c × d even though c and d are linearly independent of a and b. Also the seven dimensional cross product
Seven dimensional cross product
In mathematics, the seven-dimensional cross product is a bilinear operation on vectors in a seven-dimensional space. It assigns to any two vectors a, b in ℝ7 a vector a × b ∈ ℝ7...
is not compatible with the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
.
Quaternions
A quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
p is defined as the sum of a scalar t and a vector v:

The product of two quaternions and is defined by
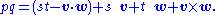
The quaternionic conjugate of q is defined by
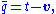
and the norm squared is
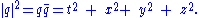
The multiplicativity of the norm in the quaternion algebra provides, for quaternions p and q:
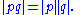
The quaternions p and q are called imaginary if their scalar part is zero; equivalently, if

Lagrange's identity is just the multiplicativity of the norm of imaginary quaternions,
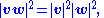
since, by definition,
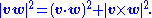
Proof of algebraic form
The vector form follows from the Binet-Cauchy identity by setting ci = ai and di = bi. The second version follows by letting ci and di denote the complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
s of ai and bi, respectively,
Here is also a direct proof. The expansion of the first term on the left side is:
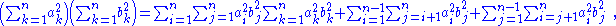
which means that the product of a column of as and a row of bs yields (a sum of elements of) a square of abs, which can be broken up into a diagonal and a pair of triangles on either side of the diagonal.
The second term on the left side of Lagrange's identity can be expanded as:
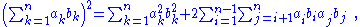
which means that a symmetric square can be broken up into its diagonal and a pair of equal triangles on either side of the diagonal.
To expand the summation on the right side of Lagrange's identity, first expand the square within the summation:
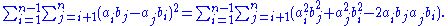
Distribute the summation on the right side,
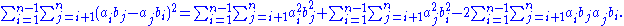
Now exchange the indices i and j of the second term on the right side, and permute the b factors of the third term, yielding:
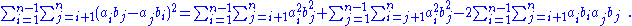
Back to the left side of Lagrange's identity: it has two terms, given in expanded form by Equations () and (). The first term on the right side of Equation () ends up canceling out the first term on the right side of Equation (), yielding
- () - () =
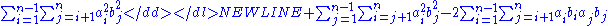
which is the same as Equation (), so Lagrange's identity is indeed an identity, Q.E.D.Q.E.D.Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
.
See also
- Brahmagupta–Fibonacci identity
- Lagrange's identity (boundary value problem)Lagrange's identity (boundary value problem)In the study of ordinary differential equations and their associated boundary value problems, Lagrange's identity, named after Joseph Louis Lagrange, gives the boundary terms arising from integration by parts of a self-adjoint linear differential operator. Lagrange's identity is fundamental in...
- Binet–Cauchy identity

