
Knaster–Tarski theorem
Encyclopedia
In the mathematical
areas of order
and lattice theory, the Knaster–Tarski theorem, named after Bronisław Knaster and Alfred Tarski
, states the following:
It was Tarski who stated the result in its most general form, and so the theorem is often known as Tarski's fixed point theorem. Some time earlier, Knaster and Tarski established the result for the special case where L is the lattice of subsets of a set, the power set lattice.
The theorem has important applications in formal semantics of programming languages
.
A kind of converse of this theorem was proved by Anne C. Davis: If every order preserving function f : L → L on a lattice
L has a fixed point, then L is a complete lattice.
, the theorem in particular guarantees the existence of at least one fixed point of f, and even the existence of a least (or greatest) fixed point. In many practical cases, this is the most important implication of the theorem.
The least fixpoint of f is the least element x such that f(x) = x, or, equivalently, such that f(x) ≤ x; the dual
holds for the greatest fixpoint, the greatest element x such that f(x) = x.
If f(lim xn)=lim f(xn) for all ascending sequences xn, then the least fixpoint of f is lim fn(0) where 0 is the least element of L, thus giving a more "constructive" version of the theorem. (See: Kleene fixed-point theorem.) More generally, if f is monotonic, then the least fixpoint of f is the stationary limit of fα(0), taking α over the ordinals
, where fα is defined by transfinite induction
: fα+1 = f ( fα) and fγ for a limit ordinal γ is the least upper bound of the fβ for all β ordinals less than γ. The dual theorem holds for the greatest fixpoint.
For example, in theoretical computer science
, least fixed point
s of monotone functions are used to define program semantics. Often a more specialized version of the theorem is used, where L is assumed to be the lattice of all subset
s of a certain set ordered by subset inclusion. This reflects the fact that in many applications only such lattices are considered. One then usually is looking for the smallest set that has the property of being a fixed point of the function f. Abstract interpretation
makes ample use of the Knaster–Tarski theorem and the formulas giving the least and greatest fixpoints.
Knaster–Tarski theorem can be used for a simple proof of Cantor–Bernstein–Schroeder theorem
.
This can be applied to obtain various theorems on invariant sets, e.g. the Ok's theorem:
In particular, using the Knaster-Tarski principle one can develop the theory of global attractors for noncontractive discontinuous (multivalued) iterated function system
s. For weakly contractive iterated function systems Kantorovitch fixpoint theorem suffices.
Other applications of fixed point principles for ordered sets come from the theory of differential, integral and operator equations.
For a complete lattice and a monotone function
and a monotone function 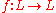 on L, the set of all fixpoints of f is also complete lattice
on L, the set of all fixpoints of f is also complete lattice 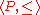 , with:
, with:
Proof. We begin by showing that P has least and greatest element. Let D = { x | x ≤ f(x) } and x ∈ D (we know that at least 0L belongs to D). Then because f is monotone we have f(x) ≤ f(f(x)), that is f(x) ∈ D.
Now let u = ∪D. Then x ≤ u and f(x) ≤ f(u), so x ≤ f(x) ≤ f(u). Therefore f(u) is an upper bound of D, but u is the least upper bound, so u ≤ f(u), i.e. u ∈ D. Then f(u) ∈ D and f(u) ≤ u from which follows f(u) = u. Because every fixpoint is in D we have that u is the greatest fixpoint of f.
The function f is monotone on the dual (complete) lattice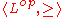 . As we have just proved, its greatest fixpoint there exists. It is the least one on L, so P has least and greatest elements, or more generally that every monotone function on a complete lattice has least and greatest fixpoints.
. As we have just proved, its greatest fixpoint there exists. It is the least one on L, so P has least and greatest elements, or more generally that every monotone function on a complete lattice has least and greatest fixpoints.
If a ∈ L and b ∈ L, we'll write [a, b] for the closed interval with bounds a and b: { x ∈ L | a ≤ x ≤ b }. The closed intervals are also complete lattices.
It remains to be proven that P is complete lattice. Let 1L = ∪L, W ⊆ P and w = ∪W. We′ll show that f([w, 1L]) ⊆ [w, 1L]. Indeed for every x ∈ W we have x = f(x) ≤ f(w). Since w is the least upper bound of W, w ≤ f(w). Then from y ∈ [w, 1L] follows that w ≤ f(w) ≤ f(y), giving f(y) ∈ [w, 1L] or simply f([w, 1L]) ⊆ [w, 1L]. This allow us to look at f as a function on the complete lattice [w, 1L]. Then it has least fixpoint there, giving us the least upper bound of W. We′ve shown that arbitrary subset of P has supremum which turns P into complete lattice.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
areas of order
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
and lattice theory, the Knaster–Tarski theorem, named after Bronisław Knaster and Alfred Tarski
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
, states the following:
- Let L be a complete latticeComplete latticeIn mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
and let f : L → L be an order-preserving functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. Then the set of fixed pointFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s of f in L is also a complete lattice.
It was Tarski who stated the result in its most general form, and so the theorem is often known as Tarski's fixed point theorem. Some time earlier, Knaster and Tarski established the result for the special case where L is the lattice of subsets of a set, the power set lattice.
The theorem has important applications in formal semantics of programming languages
Formal semantics of programming languages
In programming language theory, semantics is the field concerned with the rigorous mathematical study of the meaning of programming languages and models of computation...
.
A kind of converse of this theorem was proved by Anne C. Davis: If every order preserving function f : L → L on a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
L has a fixed point, then L is a complete lattice.
Consequences: least and greatest fixed points
Since complete lattices cannot be emptyEmpty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, the theorem in particular guarantees the existence of at least one fixed point of f, and even the existence of a least (or greatest) fixed point. In many practical cases, this is the most important implication of the theorem.
The least fixpoint of f is the least element x such that f(x) = x, or, equivalently, such that f(x) ≤ x; the dual
Duality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
holds for the greatest fixpoint, the greatest element x such that f(x) = x.
If f(lim xn)=lim f(xn) for all ascending sequences xn, then the least fixpoint of f is lim fn(0) where 0 is the least element of L, thus giving a more "constructive" version of the theorem. (See: Kleene fixed-point theorem.) More generally, if f is monotonic, then the least fixpoint of f is the stationary limit of fα(0), taking α over the ordinals
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
, where fα is defined by transfinite induction
Transfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
: fα+1 = f ( fα) and fγ for a limit ordinal γ is the least upper bound of the fβ for all β ordinals less than γ. The dual theorem holds for the greatest fixpoint.
For example, in theoretical computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, least fixed point
Least fixed point
In order theory, a branch of mathematics, the least fixed point of a function is the fixed point which is less than or equal to all other fixed points, according to some partial order....
s of monotone functions are used to define program semantics. Often a more specialized version of the theorem is used, where L is assumed to be the lattice of all subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of a certain set ordered by subset inclusion. This reflects the fact that in many applications only such lattices are considered. One then usually is looking for the smallest set that has the property of being a fixed point of the function f. Abstract interpretation
Abstract interpretation
In computer science, abstract interpretation is a theory of sound approximation of the semantics of computer programs, based on monotonic functions over ordered sets, especially lattices. It can be viewed as a partial execution of a computer program which gains information about its semantics In...
makes ample use of the Knaster–Tarski theorem and the formulas giving the least and greatest fixpoints.
Knaster–Tarski theorem can be used for a simple proof of Cantor–Bernstein–Schroeder theorem
Cantor–Bernstein–Schroeder theorem
In set theory, the Cantor–Bernstein–Schroeder theorem, named after Georg Cantor, Felix Bernstein, and Ernst Schröder, states that, if there exist injective functions and between the sets A and B, then there exists a bijective function...
.
Weaker versions of the theorem
Weaker versions of the Knaster–Tarski theorem can be formulated for ordered sets, but involve more complicated assumptions. For example:- Let L be a partially ordered setPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
with the smallest element (bottom) and let f : L → L be an order-preservingMonotonic functionIn mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. Further, suppose there exists u in L such that f(u) ≤ u and that any chain in the subset {x in L : x ≤ f(x), x ≤ u} has supremum. Then f admits the least fixed pointFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
.
This can be applied to obtain various theorems on invariant sets, e.g. the Ok's theorem:
- For the monotone map F : P(X) → P(X) on the family of (closed) nonempty subsets of X the following are equivalent: (o) F admits A in P(X) s.t.
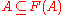 , (i) F admits invariant set A in P(X) i.e.
, (i) F admits invariant set A in P(X) i.e. 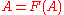 , (ii) F admits maximal invariant set A, (ii) F admits the greatest invariant set A.
, (ii) F admits maximal invariant set A, (ii) F admits the greatest invariant set A.
In particular, using the Knaster-Tarski principle one can develop the theory of global attractors for noncontractive discontinuous (multivalued) iterated function system
Iterated function system
In mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar....
s. For weakly contractive iterated function systems Kantorovitch fixpoint theorem suffices.
Other applications of fixed point principles for ordered sets come from the theory of differential, integral and operator equations.
Proof
Let's restate the theorem.For a complete lattice
 and a monotone function
and a monotone function 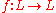 on L, the set of all fixpoints of f is also complete lattice
on L, the set of all fixpoints of f is also complete lattice 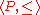 , with:
, with:
-
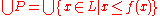 as the greatest fixpoint of f
as the greatest fixpoint of f -
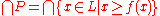 as the least fixpoint of f.
as the least fixpoint of f.
Proof. We begin by showing that P has least and greatest element. Let D = { x | x ≤ f(x) } and x ∈ D (we know that at least 0L belongs to D). Then because f is monotone we have f(x) ≤ f(f(x)), that is f(x) ∈ D.
Now let u = ∪D. Then x ≤ u and f(x) ≤ f(u), so x ≤ f(x) ≤ f(u). Therefore f(u) is an upper bound of D, but u is the least upper bound, so u ≤ f(u), i.e. u ∈ D. Then f(u) ∈ D and f(u) ≤ u from which follows f(u) = u. Because every fixpoint is in D we have that u is the greatest fixpoint of f.
The function f is monotone on the dual (complete) lattice
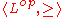 . As we have just proved, its greatest fixpoint there exists. It is the least one on L, so P has least and greatest elements, or more generally that every monotone function on a complete lattice has least and greatest fixpoints.
. As we have just proved, its greatest fixpoint there exists. It is the least one on L, so P has least and greatest elements, or more generally that every monotone function on a complete lattice has least and greatest fixpoints.If a ∈ L and b ∈ L, we'll write [a, b] for the closed interval with bounds a and b: { x ∈ L | a ≤ x ≤ b }. The closed intervals are also complete lattices.
It remains to be proven that P is complete lattice. Let 1L = ∪L, W ⊆ P and w = ∪W. We′ll show that f([w, 1L]) ⊆ [w, 1L]. Indeed for every x ∈ W we have x = f(x) ≤ f(w). Since w is the least upper bound of W, w ≤ f(w). Then from y ∈ [w, 1L] follows that w ≤ f(w) ≤ f(y), giving f(y) ∈ [w, 1L] or simply f([w, 1L]) ⊆ [w, 1L]. This allow us to look at f as a function on the complete lattice [w, 1L]. Then it has least fixpoint there, giving us the least upper bound of W. We′ve shown that arbitrary subset of P has supremum which turns P into complete lattice.
See also
- Kleene fixpoint theoremKleene fixpoint theoremIn the mathematical areas of order and lattice theory, the Kleene fixed-point theorem, named after American mathematician Stephen Cole Kleene, states the following:...
- Kantorovitch fixpoint theorem (known also as Tarski-Kantorovitch fixpoint principle)
- Modal μ-calculus
External links
- J. B. Nation, Notes on lattice theory.

