
Kleene fixpoint theorem
Encyclopedia
In the mathematical
areas of order
and lattice theory, the Kleene fixed-point theorem, named after American mathematician Stephen Cole Kleene
, states the following:
It is often attributed to Alfred Tarski
, but the original statement of Tarski's fixed point theorem is about monotone functions on complete lattices.
The ascending Kleene chain of f is the chain
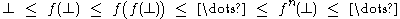
obtained by iterating
f on the least element ⊥ of L. Expressed in a formula, the theorem states that
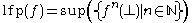
where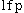 denotes the least fixed point.
denotes the least fixed point.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
areas of order
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
and lattice theory, the Kleene fixed-point theorem, named after American mathematician Stephen Cole Kleene
Stephen Cole Kleene
Stephen Cole Kleene was an American mathematician who helped lay the foundations for theoretical computer science...
, states the following:
- Let L be a complete partial orderComplete partial orderIn mathematics, directed complete partial orders and ω-complete partial orders are special classes of partially ordered sets, characterized by particular completeness properties...
, and let f : L → L be a continuousScott continuityIn mathematics, given two partially ordered sets P and Q a function f : P \rightarrow Q between them is Scott-continuous if it preserves all directed suprema, i.e...
(and therefore monotone) functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. Then the least fixed pointLeast fixed pointIn order theory, a branch of mathematics, the least fixed point of a function is the fixed point which is less than or equal to all other fixed points, according to some partial order....
of f is the supremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of the ascending Kleene chain of f.
It is often attributed to Alfred Tarski
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
, but the original statement of Tarski's fixed point theorem is about monotone functions on complete lattices.
The ascending Kleene chain of f is the chain
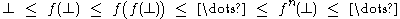
obtained by iterating
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
f on the least element ⊥ of L. Expressed in a formula, the theorem states that
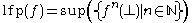
where
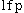 denotes the least fixed point.
denotes the least fixed point.

