
Kirchhoff's theorem
Encyclopedia
In the mathematical
field of graph theory
Kirchhoff's theorem or Kirchhoff's matrix tree theorem named after Gustav Kirchhoff
is a theorem about the number of spanning tree
s in a graph
. It is a generalization of Cayley's formula which provides the number of spanning trees in a complete graph
.
of a graph that is equal to the difference between the graph's degree matrix
(a diagonal matrix with vertex degrees on the diagonals) and its adjacency matrix
(a (0,1)-matrix with 1's at places corresponding to entries where the vertices are adjacent and 0's otherwise).
For a given connected graph G with n labeled vertices
, let λ1, λ2, ..., λn−1 be the non-zero eigenvalues of its Laplacian matrix. Then the number of spanning trees of G is
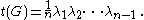
Equivalently the number of spanning trees is equal to the absolute value of any cofactor of the Laplacian matrix of G.
 We first construct the Laplacian matrix
We first construct the Laplacian matrix
Q for the example kite graph G (see image at right):
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
Kirchhoff's theorem or Kirchhoff's matrix tree theorem named after Gustav Kirchhoff
Gustav Kirchhoff
Gustav Robert Kirchhoff was a German physicist who contributed to the fundamental understanding of electrical circuits, spectroscopy, and the emission of black-body radiation by heated objects...
is a theorem about the number of spanning tree
Spanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
s in a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. It is a generalization of Cayley's formula which provides the number of spanning trees in a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
.
Kirchhoff's theorem
Kirchhoff's theorem relies on the notion of the Laplacian matrixLaplacian matrix
In the mathematical field of graph theory the Laplacian matrix, sometimes called admittance matrix or Kirchhoff matrix, is a matrix representation of a graph. Together with Kirchhoff's theorem it can be used to calculate the number of spanning trees for a given graph. The Laplacian matrix can be...
of a graph that is equal to the difference between the graph's degree matrix
Degree matrix
In the mathematical field of graph theory the degree matrix is a diagonal matrix which contains information about the degree of each vertex. It is used together with the adjacency matrix to construct the Laplacian matrix of a graph.-Definition:...
(a diagonal matrix with vertex degrees on the diagonals) and its adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
(a (0,1)-matrix with 1's at places corresponding to entries where the vertices are adjacent and 0's otherwise).
For a given connected graph G with n labeled vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
, let λ1, λ2, ..., λn−1 be the non-zero eigenvalues of its Laplacian matrix. Then the number of spanning trees of G is
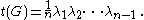
Equivalently the number of spanning trees is equal to the absolute value of any cofactor of the Laplacian matrix of G.
An example using the matrix-tree theorem

Laplacian matrix
In the mathematical field of graph theory the Laplacian matrix, sometimes called admittance matrix or Kirchhoff matrix, is a matrix representation of a graph. Together with Kirchhoff's theorem it can be used to calculate the number of spanning trees for a given graph. The Laplacian matrix can be...
Q for the example kite graph G (see image at right):
-
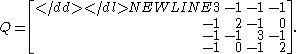
We now construct a matrix Q* by deleting any row s and any column t (s and t not necessarily distinct) from Q. For this example, we will delete row 1 and column 1 to obtain
-
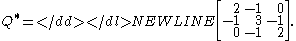
Finally, we take the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of Q* to obtain t(G). t(G) is thus the (1,1) cofactor of Q. In this example t(G) is 8.
Proof outline
First notice that the Laplacian has the property that the sum of its entries across any row and any column is 0. Thus we can transform any minor into any other minor by adding rows and columns, switching them, and multiplying a row or a column by −1. Thus the cofactors are the same up to sign, and it can be verified that, in fact, they have the same sign.
We proceed to show that the determinant of the minor M11 counts the number of spanning trees. Let n be the number of vertices of the graph, and m the number of its edges. The incidence matrix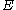 is an n-by-m matrix. Suppose that (i, j) is the kth edge of the graph, and that i < j. Then Eik = 1, Ejk = −1, and all other entries in column k are 0. For the preceding example (with n = 4 and m = 5):
is an n-by-m matrix. Suppose that (i, j) is the kth edge of the graph, and that i < j. Then Eik = 1, Ejk = −1, and all other entries in column k are 0. For the preceding example (with n = 4 and m = 5):
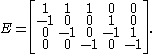
Recall that the Laplacian L can be factored into the product of the incidence matrixIncidence matrixIn mathematics, an incidence matrix is a matrix that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related ...
and its transpose, i.e., L = EET. Furthermore, let F be the matrix E with its first row deleted, so that FFT = M11.
Now the Cauchy-Binet formulaCauchy-Binet formulaIn linear algebra, the Cauchy–Binet formula, named after Augustin-Louis Cauchy and Jacques Philippe Marie Binet, is an identity for the determinant of the product of two rectangular matrices of transpose shapes . It generalizes the statement that the determinant of a product of square matrices is...
allows us to write
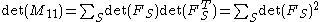
where S ranges across subsets of [m] \ {1} of size n − 1, and FS denotes the (n − 1)-by-(n − 1) matrix whose columns are those of F with index in S. Then every S specifies n − 1 edges of the original graph, and it can be shown that those edges induce a spanning tree iff the determinant of FS is +1 or −1, and that they do not induce a spanning tree iff the determinant is 0. This completes the proof.
Cayley's formula
Cayley's formula follows from Kirchhoff's theorem as a special case, since every vector with 1 in one place, −1 in another place, and 0 elsewhere is an eigenvector of the Laplacian matrix of the complete graph, with the corresponding eigenvalue being n. These vectors together span a space of dimension n − 1, so there are no other non-zero eigenvalues.
Alternatively, note that as Cayley's formula counts the number of distinct labeled trees of a complete graph Kn we need to compute any cofactor of the Laplacian matrix of Kn. The Laplacian matrix in this case is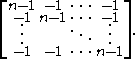
It can be easily verified that any cofactor of the above matrix is nn−2 which is Cayley's formula.
Kirchhoff's theorem for multigraphs
Kirchhoff's theorem holds for multigraphMultigraphIn mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
s as well; the matrix Q is modified as follows:- if vertex i is adjacent to vertex j in G, qi,j equals −m, where m is the number of edges between i and j;
- when counting the degree of a vertex, all loopsLoop (graph theory)In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....
are excluded.
Explicit enumeration of spanning trees
Kirchhoff's theorem can be strengthened by altering the definition of the Laplacian matrix. Rather than merely counting edges emanating from each vertex or connecting a pair of vertices, label each edge with an indeterminant and let the (i,j)-th entry of the modified Laplacian matrix be the sum over the indeterminants corresponding to edges between the i-th and j-th vertices when i does not equal j, and the negative sum over all indeterminants corresponding to edges emanating from the i-th vertex when i equals j.
The determinant above is then a homogeneous polynomialHomogeneous polynomialIn mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
(the Kirchhoff polynomial) in the indeterminants corresponding to the edges of the graph. After collecting terms and performing all possible cancellations, each monomialMonomialIn mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
in the resulting expression represents a spanning tree consisting of the edges corresponding to the indeterminants appearing in that monomial. In this way, one can obtain explicit enumeration of all the spanning trees of the graph simply by computing the determinant.
See also
- Prufer sequences
- Minimum spanning treeMinimum spanning treeGiven a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees...
- List of topics related to trees
External links
-

