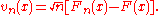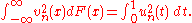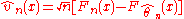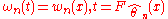Khmaladze transformation
Encyclopedia
The Khmaladze Transformation is a statistical tool.
Consider the sequence of empirical distribution function
s
based on a
sequence of i.i.d random variables,
, as n increases.
Suppose
is the hypothetical distribution function
of
each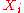
. To test whether the choice of 
is correct or not, statisticians use the normalized difference,
This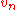
, as a random process in 
, is called the empirical process
. Various functional
s of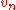
are used as test statistics. The change of the variable 
, , 
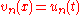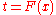transforms to the so-called uniform empirical process 
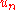. The latter is an empirical processes based on independent random variables 
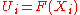, which are uniformly distributed
on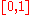
if the 
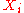s do indeed have distribution function 
.
This fact was discovered and first utilized by Kolmogorov(1933), Wald and Wolfowitz(1936) and Smirnov(1937) and, especially after Doob(1949) and Anderson and Darling(1952), it led to the standard rule to choose test statistics based on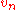
. That is, test statistics 
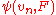are defined (which possibly depend on the 
being tested) in such a way that there exists another statistic 
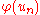derived from the uniform empirical process, such that 
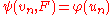. Examples are
and
For all such functionals, their null distribution
(under the hypothetical
) does not depend on 
, and can be calculated once and then used to test any 
.
However, it is only rarely that one needs to test a simple hypothesis, when a fixed
as a hypothesis is given. Much more often, one needs to verify parametric hypotheses where the hypothetical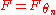 
, depends on some parameters 
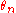, which the hypothesis does not specify and which have to be estimated from the sample 
itself.
Although the estimators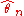
, most commonly converge to true value of 
, it was discovered (Kac, Kiefer and Wolfowitz(1955) and Gikhman(1954)) that the parametric, or estimated, empirical process
differs significantly from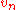
and that the transformed process 
, 
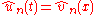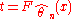has a distribution for which the limit distribution, as 
, is dependent on the parametric form of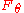 
and on the particular estimator 
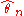and, in general, within one parametric family
, on the value of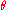
.
From mid-50's to the late-80's, much work was done to clarify the situation and understand the nature of the process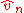
.
In 1981, and then 1987 and 1993, E. V. Khmaladze suggested to replace the parametric empirical process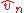
by its martingale part 
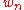only.
where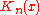
is the compensator of 
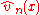. Then the following properties of 
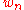were established:
is that of standard Brownian motion on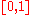
, i.e., is
again standard and independent of the choice of
.
For a long time the transformation was, although known, still not used. Later, the work of researchers like R. Koenker, W. Stute, J. Bai, H. Koul, A. Koening, ... and others made it popular in econometrics and other fields of statistics.
Consider the sequence of empirical distribution function
Empirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
s
based on asequence of i.i.d random variables,
, as n increases.Suppose
is the hypothetical distribution functionDistribution function
In molecular kinetic theory in physics, a particle's distribution function is a function of seven variables, f, which gives the number of particles per unit volume in phase space. It is the number of particles per unit volume having approximately the velocity near the place and time...
of
each
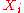. To test whether the choice of is correct or not, statisticians use the normalized difference,
This
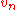, as a random process in , is called the empirical processEmpirical process
The study of empirical processes is a branch of mathematical statistics and a sub-area of probability theory. It is a generalization of the central limit theorem for empirical measures...
. Various functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
s of
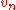are used as test statistics. The change of the variable 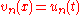, , 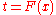transforms to the so-called uniform empirical process 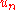. The latter is an empirical processes based on independent random variables 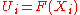, which are uniformly distributedUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on
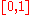if the 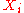s do indeed have distribution function .This fact was discovered and first utilized by Kolmogorov(1933), Wald and Wolfowitz(1936) and Smirnov(1937) and, especially after Doob(1949) and Anderson and Darling(1952), it led to the standard rule to choose test statistics based on
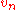. That is, test statistics 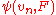are defined (which possibly depend on the being tested) in such a way that there exists another statistic 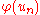derived from the uniform empirical process, such that 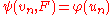. Examples are
and
For all such functionals, their null distribution
Null distribution
In statistical hypothesis testing, the null distribution is the probability distribution of the test statistic when the null hypothesis is true.In an F-test, the null distribution is an F-distribution....
(under the hypothetical
) does not depend on , and can be calculated once and then used to test any .However, it is only rarely that one needs to test a simple hypothesis, when a fixed
as a hypothesis is given. Much more often, one needs to verify parametric hypotheses where the hypothetical 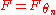, depends on some parameters 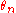, which the hypothesis does not specify and which have to be estimated from the sample itself.Although the estimators
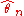, most commonly converge to true value of , it was discovered (Kac, Kiefer and Wolfowitz(1955) and Gikhman(1954)) that the parametric, or estimated, empirical process
differs significantly from
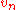and that the transformed process 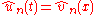, 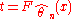has a distribution for which the limit distribution, as , is dependent on the parametric form of 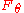and on the particular estimator 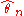and, in general, within one parametric familyParametric family
In mathematics and its applications, a parametric family or a parameterized family is a family of objects whose definitions depend on a set of parameters....
, on the value of
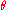.From mid-50's to the late-80's, much work was done to clarify the situation and understand the nature of the process
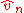.In 1981, and then 1987 and 1993, E. V. Khmaladze suggested to replace the parametric empirical process
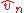by its martingale part 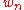only.
where
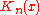is the compensator of 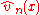. Then the following properties of 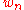were established:- Although the form of
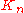, and therefore, of 
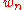, depends on 
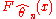, as a function of both 
and 
, the limit distribution of the time transformed process
is that of standard Brownian motion on
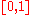, i.e., isagain standard and independent of the choice of
.- The relationship between
and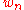 
and between their limits, is one to one, so that the statistical inference based on 
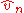or on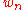 
are equivalent, and in 
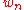, nothing is lost compared to 
.
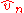- The construction of innovation martingale
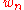could be carried over to the case of vector-valued 
, giving rise to the definition of the so-called scanning martingales in 
.
For a long time the transformation was, although known, still not used. Later, the work of researchers like R. Koenker, W. Stute, J. Bai, H. Koul, A. Koening, ... and others made it popular in econometrics and other fields of statistics.