
KdV hierarchy
Encyclopedia
In mathematics, the KdV hierarchy is an infinite sequence of partial differential equation
s which starts with the Korteweg–de Vries equation
.
Let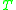 be translation operator defined on real valued functions
be translation operator defined on real valued functions
as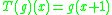 . Let
. Let  be set of all analytic function
be set of all analytic function
s that satisfy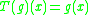 , i.e. periodic function
, i.e. periodic function
s of period 1. For each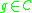 , define an operator
, define an operator
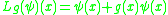
on the space of smooth function
s on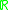 . We define the Bloch spectrum
. We define the Bloch spectrum  to be the set of
to be the set of 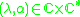 so that there is a nonzero function
so that there is a nonzero function  with
with 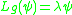 and
and 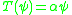 . The KdV hierarchy is a sequence of nonlinear differential operators
. The KdV hierarchy is a sequence of nonlinear differential operators 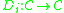 so that for any
so that for any 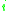 we have an analytic function
we have an analytic function 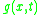 and we define
and we define 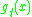 to be
to be  and
and
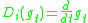 ,
,
then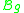 is independent of
is independent of  .
.
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s which starts with the Korteweg–de Vries equation
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
.
Let
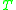 be translation operator defined on real valued functions
be translation operator defined on real valued functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
as
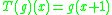 . Let
. Let  be set of all analytic function
be set of all analytic functionAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s that satisfy
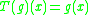 , i.e. periodic function
, i.e. periodic functionPeriodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
s of period 1. For each
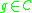 , define an operator
, define an operator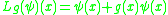
on the space of smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s on
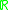 . We define the Bloch spectrum
. We define the Bloch spectrum  to be the set of
to be the set of 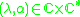 so that there is a nonzero function
so that there is a nonzero function  with
with 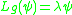 and
and 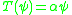 . The KdV hierarchy is a sequence of nonlinear differential operators
. The KdV hierarchy is a sequence of nonlinear differential operators 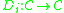 so that for any
so that for any 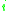 we have an analytic function
we have an analytic function 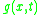 and we define
and we define 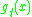 to be
to be  and
and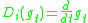 ,
,then
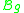 is independent of
is independent of  .
.External links
- KdV hierarchy at the Dispersive PDE Wiki.

