
Kalb-Ramond field
Encyclopedia
In theoretical physics
in general and string theory
in particular, the Kalb–Ramond field, also known as the NS-NS B-field, is a quantum field that transforms as a two-form
i.e. an antisymmetric tensor
field with two indices.
It generalizes the electromagnetic potential but it has two indices instead of one. This difference is related to the fact that the electromagnetic potential is integrated over one-dimensional worldlines of particles to obtain one of its contributions to the action while the Kalb–Ramond field must be integrated over the two-dimensional worldsheet
of the string. In particular, while the
action for a charged particle moving in an electromagnetic
potential is given by
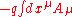
that for a string coupled to the Kalb–Ramond field has the form
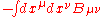
This term in the action implies that the fundamental string of string theory is a source of the NS-NS B-field much like charged particles are sources of the electromagnetic field.
The Kalb–Ramond field appears, together with the metric tensor
and dilaton
, as a set of massless excitations of a closed string.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
in general and string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
in particular, the Kalb–Ramond field, also known as the NS-NS B-field, is a quantum field that transforms as a two-form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
i.e. an antisymmetric tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
field with two indices.
It generalizes the electromagnetic potential but it has two indices instead of one. This difference is related to the fact that the electromagnetic potential is integrated over one-dimensional worldlines of particles to obtain one of its contributions to the action while the Kalb–Ramond field must be integrated over the two-dimensional worldsheet
Worldsheet
In string theory, a worldsheet is a two-dimensional manifold which describes the embedding of a string in spacetime. The term was coined by Leonard Susskind around 1967 as a direct generalization of the world line concept for a point particle in special and general relativity.The type of string,...
of the string. In particular, while the
action for a charged particle moving in an electromagnetic
potential is given by
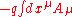
that for a string coupled to the Kalb–Ramond field has the form
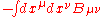
This term in the action implies that the fundamental string of string theory is a source of the NS-NS B-field much like charged particles are sources of the electromagnetic field.
The Kalb–Ramond field appears, together with the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
and dilaton
Dilaton
In particle physics, a dilaton is a hypothetical particle. It also appears in Kaluza-Klein theory's compactifications of extra dimensions when the volume of the compactified dimensions vary....
, as a set of massless excitations of a closed string.

