
Inverse curve
Encyclopedia
In geometry
, an inverse curve of a given curve C is the result of applying an inverse operation to C. Specifically, with respect to a fixed circle with center O and radius k the inverse of a point Q is the point P for which P lies on the ray OQ and OP·PQ = k2. The Inverse of the curve C is then the locus of P as Q runs over C. The point O in this construction is called the center of inversion, the circle the circle of inversion, and k the radius of inversion.
An inversion applied twice is the identity transformation, so the inverse of an inverse curve with respect to the same circle is the original curve. Points on the circle of inversion are fixed by the inversion, so its inverse is itself.
is (X, Y) where

or equivalently
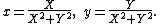
So the inverse of the curve determined by f(x, y) = 0 with respect to the unit circle is
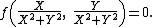
It is clear from this that the inverse of an algebraic curve of degree n is also algebraic of degree at most 2n.
Similarly, the inverse of the curve defined parametrically
by the equations

with respect to the unit circle is given parametrically as
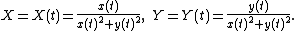
This implies that the inverse of a rational curve is also rational.
More generally, the inverse of the curve determined by f(x, y) = 0 with respect to the circle with center (a, b) and radius k is
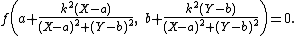
The inverse of the curve defined parametrically by

with respect to the same circle is given parametrically as
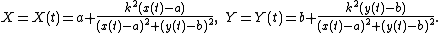
In polar coordinates, the equations are simpler when the circle of inversion is the unit circle.
The inverse of the point (r, θ) with respect to the unit circle
is (R, Θ) where

or equivalently
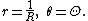
So the inverse of the curve f(r, θ) = 0 is determined by f(1/R, Θ) = 0 and the inverse of the curve r = g(θ) is r = 1/g(θ).
, meaning that it contains the circular points, (1, ±i, 0), when considered as a curve in the complex projective plane.
Specifically, if C is p-circular of degree n, and if the center of inversion is a singularity of order q on C, then the inverse curve will be an (n − p − q)-circular curve of degree 2n − 2p − q and the center of inversion is a singularity of order n − 2p on the inverse curve. Here q = 0 if the curve does not contain contain the center of inversion and q = 1 if the center of inversion is a nonsingular point on it; similarly the circular points, (1, ±i, 0), are singularities of order p on C. The value k can be eliminated from these relations to show that the set of p-circular curves of degree p + k, where p may vary but k is a fixed positive integer, is invariant under inversion.

gives us

the equation of a hyperbola; since inversion is a birational transformation and the hyperbola is a rational curve, this shows the lemniscate is also a rational curve, which is to say a curve of genus
zero. If we apply it to the Fermat curve
xn + yn = 1, where n is odd, we obtain
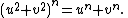
Any rational point on the Fermat curve has a corresponding rational point on this curve, giving an equivalent formulation of Fermat's Last Theorem
.
The polar equation for a line not passing through the origin is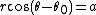
and the equation of the inverse curve is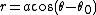
which defines a circle passing through the origin. Applying the inversion again shows that the inverse of a circle passing through the origin is a line.

where a is the radius and (r0, &theta0) are the polar coordinates of the center. The equation of the inverse curve is then

or

This is the equation a circle with radius
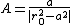
and center whose polar coordinates are
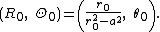
Note that R0 may be negative.
If the original circle intersects with the unit circle, then the centers of the two circles and a point of intersection form a triangle with sides 1, a, r0 this is a right triangle, i.e. the radii are at right angles, exactly when

But from the equations above, the original circle is the same as the inverse circle exactly when
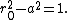
So the inverse of a circle is the same circle if and only if it intersects the unit circle at right angles.
To summarize and generalize this and the previous section:

The inverse curve then has equation
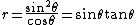
which is the cissoid of Diocles
.
with one focus at the origin is, up to similarity
where e is the eccentricity. The inverse of this curve will then be
which is the equation of a limaçon of Pascal
. When e = 0 this is the circle of inversion. When 0 < e < 1 the original curve is an ellipse and the inverse is a simple closed curve with an acnode
at the origin. When e = 1 the original curve is a parabola and the inverse is the cardioid
which has a cusp at the origin. When e > 1 the original curve is a hyperbola and the inverse forms two loops with a crunode
at the origin.
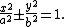
Translating this so that the origin is one of the vertices gives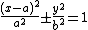
and rearranging gives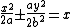
or, changing constants,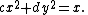
Note that parabola above now fits into this scheme by putting c = 0 and d = 1.
The equation of the inverse is

or
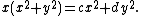
This equation describes a family of curves called the conchoids of de Sluze
. This family includes, in addition to the cissoid of Diocles listed above, the trisectrix of Maclaurin
(d = −c/3) and the right strophoid (d = −c).

gives
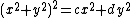
which is the hippopede
. When d = −c this is the lemniscate of Bernoulli
.
, cardioid
, oval of Cassini, strophoid
, and trisectrix of Maclaurin
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, an inverse curve of a given curve C is the result of applying an inverse operation to C. Specifically, with respect to a fixed circle with center O and radius k the inverse of a point Q is the point P for which P lies on the ray OQ and OP·PQ = k2. The Inverse of the curve C is then the locus of P as Q runs over C. The point O in this construction is called the center of inversion, the circle the circle of inversion, and k the radius of inversion.
An inversion applied twice is the identity transformation, so the inverse of an inverse curve with respect to the same circle is the original curve. Points on the circle of inversion are fixed by the inversion, so its inverse is itself.
Equations
The inverse of the point (x, y) with respect to the unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
is (X, Y) where

or equivalently
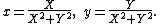
So the inverse of the curve determined by f(x, y) = 0 with respect to the unit circle is
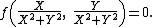
It is clear from this that the inverse of an algebraic curve of degree n is also algebraic of degree at most 2n.
Similarly, the inverse of the curve defined parametrically
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
by the equations

with respect to the unit circle is given parametrically as
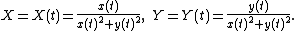
This implies that the inverse of a rational curve is also rational.
More generally, the inverse of the curve determined by f(x, y) = 0 with respect to the circle with center (a, b) and radius k is
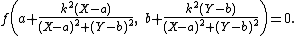
The inverse of the curve defined parametrically by

with respect to the same circle is given parametrically as
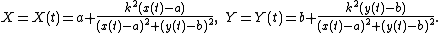
In polar coordinates, the equations are simpler when the circle of inversion is the unit circle.
The inverse of the point (r, θ) with respect to the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
is (R, Θ) where

or equivalently
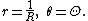
So the inverse of the curve f(r, θ) = 0 is determined by f(1/R, Θ) = 0 and the inverse of the curve r = g(θ) is r = 1/g(θ).
Degrees
As noted above, the inverse of a curve of degree n has degree at most 2n. The degree is exactly 2n unless the original curve passes through the point of inversion or it's circularCircular algebraic curve
In geometry, a circular algebraic curve is a type of plane algebraic curve determined by an equation F = 0, where F is a polynomial with real coefficients and the highest-order terms of F form a polynomial divisible by x2 + y2...
, meaning that it contains the circular points, (1, ±i, 0), when considered as a curve in the complex projective plane.
Specifically, if C is p-circular of degree n, and if the center of inversion is a singularity of order q on C, then the inverse curve will be an (n − p − q)-circular curve of degree 2n − 2p − q and the center of inversion is a singularity of order n − 2p on the inverse curve. Here q = 0 if the curve does not contain contain the center of inversion and q = 1 if the center of inversion is a nonsingular point on it; similarly the circular points, (1, ±i, 0), are singularities of order p on C. The value k can be eliminated from these relations to show that the set of p-circular curves of degree p + k, where p may vary but k is a fixed positive integer, is invariant under inversion.
Examples
Applying the above transformation to the lemniscate of BernoulliLemniscate of Bernoulli
In geometry, the lemniscate of Bernoulli is a plane curve defined from two given points F1 and F2, known as foci, at distance 2a from each other as the locus of points P so that PF1·PF2 = a2. The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from lemniscus, which is...

gives us

the equation of a hyperbola; since inversion is a birational transformation and the hyperbola is a rational curve, this shows the lemniscate is also a rational curve, which is to say a curve of genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
zero. If we apply it to the Fermat curve
Fermat curve
In mathematics, the Fermat curve is the algebraic curve in the complex projective plane defined in homogeneous coordinates by the Fermat equationX^n + Y^n = Z^n.\ Therefore in terms of the affine plane its equation is...
xn + yn = 1, where n is odd, we obtain
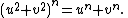
Any rational point on the Fermat curve has a corresponding rational point on this curve, giving an equivalent formulation of Fermat's Last Theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
.
Particular cases
For simplicity, the circle of inversion in the following cases will be the unit circle. Results for other circles of inversion can be found by translation and magnification of the original curve.Lines
For a line passing through the origin, the polar equation is θ = θ0 where θ0 is fixed. This remains unchanged under the inversion.The polar equation for a line not passing through the origin is
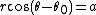
and the equation of the inverse curve is
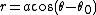
which defines a circle passing through the origin. Applying the inversion again shows that the inverse of a circle passing through the origin is a line.
Circles
In polar coordinates, the general equation for a circle that does not pass though the origin (the other cases having been covered) is
where a is the radius and (r0, &theta0) are the polar coordinates of the center. The equation of the inverse curve is then

or

This is the equation a circle with radius
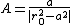
and center whose polar coordinates are
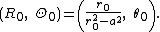
Note that R0 may be negative.
If the original circle intersects with the unit circle, then the centers of the two circles and a point of intersection form a triangle with sides 1, a, r0 this is a right triangle, i.e. the radii are at right angles, exactly when

But from the equations above, the original circle is the same as the inverse circle exactly when
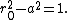
So the inverse of a circle is the same circle if and only if it intersects the unit circle at right angles.
To summarize and generalize this and the previous section:
- The inverse of a line or a circle is a line or a circle.
- If the original curve is a line then the inverse curve will pass through the center of inversion. If the original curve passes through the center of inversion then the inverted curve will be a line.
- The inverted curve will be the same as the original exactly when the curve intersects the circle of inversion at right angles.
Parabolas with center of inversion at the vertex
The equation of a parabola is, up to similarity, translating so that the vertex is at the origin and rotating so that the axis is horizontal, x = y2. In polar coordinates this becomes
The inverse curve then has equation
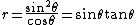
which is the cissoid of Diocles
Cissoid of Diocles
In geometry, the cissoid of Diocles is a cubic plane curve notable for the property that it can be used to construct two mean proportionals to a given ratio. In particular, it can be used to double a cube. It can be defined as the cissoid of a circle and a line tangent to it with respect to the...
.
Conic sections with center of inversion at a focus
The polar equation of a conic sectionConic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
with one focus at the origin is, up to similarity
where e is the eccentricity. The inverse of this curve will then be
which is the equation of a limaçon of Pascal
Limaçon
In geometry, a limaçon or limacon , also known as a limaçon of Pascal, is defined as a roulette formed when a circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller...
. When e = 0 this is the circle of inversion. When 0 < e < 1 the original curve is an ellipse and the inverse is a simple closed curve with an acnode
Acnode
An acnode is an isolated point not on a curve, but whose coordinates satisfy the equation of the curve. The term "isolated point" or "hermit point" is an equivalent term....
at the origin. When e = 1 the original curve is a parabola and the inverse is the cardioid
Cardioid
A cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It is therefore a type of limaçon and can also be defined as an epicycloid having a single cusp...
which has a cusp at the origin. When e > 1 the original curve is a hyperbola and the inverse forms two loops with a crunode
Crunode
A crunode is a point where a curve intersects itself so that both branches of the curve have distinct tangent lines.For a plane curve, defined as the locus of points f = 0, where f is a smooth function of variables x and y ranging over the real numbers, a crunode of the curve is a singularity of...
at the origin.
Ellipses and hyperbolas with center of inversion at a vertex
The general equation of an ellipse or hyperbola is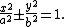
Translating this so that the origin is one of the vertices gives
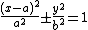
and rearranging gives
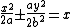
or, changing constants,
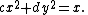
Note that parabola above now fits into this scheme by putting c = 0 and d = 1.
The equation of the inverse is

or
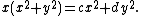
This equation describes a family of curves called the conchoids of de Sluze
Conchoid of de Sluze
The conchoid of de Sluze is a family of plane curves studied in 1662 by René François Walter, baron de Sluze.The curves are defined by the polar equationr=\sec\theta+a\cos\theta \,....
. This family includes, in addition to the cissoid of Diocles listed above, the trisectrix of Maclaurin
Trisectrix of Maclaurin
In geometry, the trisectrix of Maclaurin is a cubic plane curve notable for its trisectrix property, meaning it can be used to trisect an angle. It can be defined as locus of the points of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the...
(d = −c/3) and the right strophoid (d = −c).
Ellipses and hyperbolas with center of inversion at the center
Inverting the equation of an ellipse or hyperbola
gives
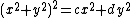
which is the hippopede
Hippopede
In geometry, a hippopede is a plane curve determined by an equation of the form^2=cx^2+dy^2,...
. When d = −c this is the lemniscate of Bernoulli
Lemniscate of Bernoulli
In geometry, the lemniscate of Bernoulli is a plane curve defined from two given points F1 and F2, known as foci, at distance 2a from each other as the locus of points P so that PF1·PF2 = a2. The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from lemniscus, which is...
.
Conics with arbitrary center of inversion
Applying the degree formula above, the inverse of a conic (other than a circle) is a circular cubic if the center of inversion is on the curve, and a bicircular quartic otherwise. Conics are rational so the inverse curves are rational as well. Conversely, any rational circular cubic or rational bicircular quartic is the inverse of a conic. In fact, any such curve must have a real singularity and taking this point as a center of inversion, the inverse curve will be a conic by the degree formula.Anallagmatic curves
An anallagmatic curve is one which inverts into itself. Examples include the circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, cardioid
Cardioid
A cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It is therefore a type of limaçon and can also be defined as an epicycloid having a single cusp...
, oval of Cassini, strophoid
Strophoid
In geometry, a strophoid is a curve generated from a given curve C and points A and O as follows: Let L be a variable line passing through O and intersecting C at K. Now let P1 and P2 be the two points on L whose distance from K is the same as the distance from A to K...
, and trisectrix of Maclaurin
Trisectrix of Maclaurin
In geometry, the trisectrix of Maclaurin is a cubic plane curve notable for its trisectrix property, meaning it can be used to trisect an angle. It can be defined as locus of the points of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the...
.
External links
- Definition at MacTutor's Famous Curves Index. This site also has examples of inverse curves and a Java applet to explore the inverse curves of every curve in the index.



