A crunode is a point where a curve

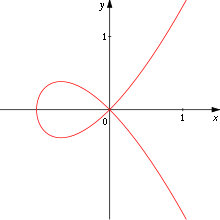
Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

 intersects itself so that both branches of the curve have distinct tangent lines.

For a plane curve, defined as the locus of points f(x, y) = 0, where f(x, y) is a smooth function

Smooth function

In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...

 of variables x and y ranging over the real numbers, a crunode of the curve is a singularity

Singularity theory

-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...

 of the function f, where both partial derivatives 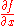and 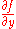vanish. Further the Hessian matrix

Hessian matrix

In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...

 of second derivatives will have both positive and negative eigenvalues.

See also

• Singular point of a curve
  Singular point of a curve
  In geometry, a singular point on a curve is one where the curve is not given by a smooth embedding of a parameter. The precise definition of a singular point depends on the type of curve being studied.-Algebraic curves in the plane:...
  
  
• Acnode
  Acnode
  An acnode is an isolated point not on a curve, but whose coordinates satisfy the equation of the curve. The term "isolated point" or "hermit point" is an equivalent term....
  
  
• Cusp
  Cusp (singularity)
  In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
  
  
• Tacnode
  Tacnode
  In geometry, a tacnode is a kind of singular point of a curve. It is defined as a point where two osculating circles to the curve at that point are tangent. This means that two branches of the curve have ordinary tangency at the double point. The canonical example is = 0...
  
  
• Saddle point
  Saddle point
  In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...