
Strophoid
Encyclopedia
In geometry
, a strophoid is a curve generated from a given curve C and points A (the fixed point) and O (the pole) as follows: Let L be a variable line passing through O and intersecting C at K. Now let P1 and P2 be the two points on L whose distance from K is the same as the distance from A to K. The locus
of such points P1 and P2 is then the strophoid of C with respect to the pole O and fixed point A. Note that AP1 and AP2 are at right angles in this construction.
In the special case where C is a line, A lies on C, and O is not on C, then the curve is called an oblique strophoid. If, in addition, OA is perpendicular to C then the curve is called a right strophoid, or simply strophoid by some authors. The right strophoid is also called the logocyclic curve or foliate.
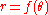 , where the origin is taken to be O. Let A be the point (a, b). If
, where the origin is taken to be O. Let A be the point (a, b). If  is a point on the curve the distance from K to A is
is a point on the curve the distance from K to A is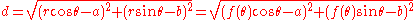 .
.
The points on the line OK have polar angle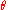 , and the points at distance d from K on this line are distance
, and the points at distance d from K on this line are distance 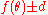 from the origin. Therefore the equation of the strophoid is given by
from the origin. Therefore the equation of the strophoid is given by
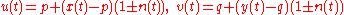 ,
,
where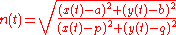 .
.
with poles O and A.
Let O be the origin and A be the point (a, 0). Let K be a point on the curve, the angle between OK and the x-axis, and
the angle between OK and the x-axis, and  the angle between AK and the x-axis. Suppose
the angle between AK and the x-axis. Suppose  can be given as a function
can be given as a function 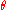 , say
, say 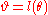 . Let
. Let  be the angle at K so
be the angle at K so 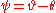 . We can determine r in terms of l using the law of sines. Since
. We can determine r in terms of l using the law of sines. Since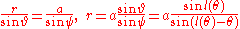 .
.
Let P1 and P2 be the points on OK that are distance AK from K, numbering so that and
and  .
. 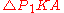 is isosceles with vertex angle
is isosceles with vertex angle 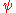 , so the remaining angles,
, so the remaining angles, 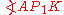 and
and 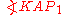 , are
, are 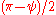 . The angle between AP1 and the x-axis is then
. The angle between AP1 and the x-axis is then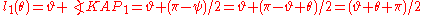 .
.
By a similar argument, or simply using the fact that AP1 and AP2 are at right angles, the angle between AP2 and the x-axis is then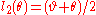 .
.
The polar equation for the strophoid can now be derived from l1 and l2 from the formula above: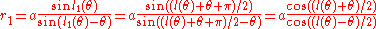

C is a sectrix of Maclaurin with poles O and A when l is of the form , in that case l1 and l2 will have the same form so the strophoid is either another sectrix of Maclaurin or a pair of such curves. In this case there is also a simple polar equation for the polar equation if the origin is shifted to the right by a.
, in that case l1 and l2 will have the same form so the strophoid is either another sectrix of Maclaurin or a pair of such curves. In this case there is also a simple polar equation for the polar equation if the origin is shifted to the right by a.
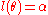 where
where  is a constant. Then
is a constant. Then  and
and  . The polar equations of the resulting strophoid, called an oblique strphoid, with the origin at O are then
. The polar equations of the resulting strophoid, called an oblique strphoid, with the origin at O are then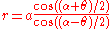
and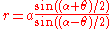 .
.
It's easy to check that these equations describe the same curve.
Moving the origin to A (again, see Sectrix of Maclaurin
) and replacing −a with a produces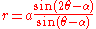 ,
,
and rotating by in turn produces
in turn produces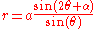 .
.
In rectangular coordinates, with a change of constant parameters, this is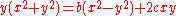 .
.
This is a cubic curve and, by the expression in polar coordinates it is rational. It has a crunode
at (0, 0) and the line y=b is an asymptote.
 in
in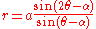
gives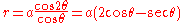 .
.
This is called the right strophoid and corresponds to the case where C is the y-axis, O is the origin, and A is the point (a,0).
The Cartesian
equation is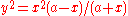 .
.
The curve resembles the Folium of Descartes
and the line x = −a is an asymptote
to two branches. The curve has two more asymptotes, in the plane with complex coordinates, given by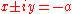 .
.
 where
where  is a constant. Then
is a constant. Then  and
and  . The polar equations of the resulting strophoid, called an oblique strphoid, with the origin at O are then
. The polar equations of the resulting strophoid, called an oblique strphoid, with the origin at O are then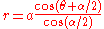
and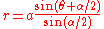 .
.
These are the equations of the two circles which also pass through O and A and form angles of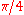 with C at these points.
with C at these points.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a strophoid is a curve generated from a given curve C and points A (the fixed point) and O (the pole) as follows: Let L be a variable line passing through O and intersecting C at K. Now let P1 and P2 be the two points on L whose distance from K is the same as the distance from A to K. The locus
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of such points P1 and P2 is then the strophoid of C with respect to the pole O and fixed point A. Note that AP1 and AP2 are at right angles in this construction.
In the special case where C is a line, A lies on C, and O is not on C, then the curve is called an oblique strophoid. If, in addition, OA is perpendicular to C then the curve is called a right strophoid, or simply strophoid by some authors. The right strophoid is also called the logocyclic curve or foliate.
Polar coordinates
Let the curve C be given by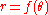 , where the origin is taken to be O. Let A be the point (a, b). If
, where the origin is taken to be O. Let A be the point (a, b). If  is a point on the curve the distance from K to A is
is a point on the curve the distance from K to A is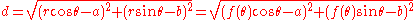 .
.The points on the line OK have polar angle
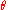 , and the points at distance d from K on this line are distance
, and the points at distance d from K on this line are distance 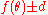 from the origin. Therefore the equation of the strophoid is given by
from the origin. Therefore the equation of the strophoid is given by
Cartesian coordinates
Let C be given parametrically by (x(t), y(t)). Let A be the point (a, b) and let O be the point (p, q). Then, by a straightforward application of the polar formula, the strophoid is given parametrically by: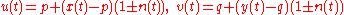 ,
,where
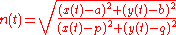 .
.An alternative polar formula
The complex nature of the formulas given above limits their usefulness in specific cases. There is an alternative form which is sometimes simpler to apply. This is particularly useful when C is a sectrix of MaclaurinSectrix of Maclaurin
In geometry, a sectrix of Maclaurin is defined as the curve swept out by the point of intersection of two lines which are each revolving at constant rates about different points called poles. Equivalently, a sectrix of Maclaurin can be defined as a curve whose equation in biangular coordinates is...
with poles O and A.
Let O be the origin and A be the point (a, 0). Let K be a point on the curve,
 the angle between OK and the x-axis, and
the angle between OK and the x-axis, and  the angle between AK and the x-axis. Suppose
the angle between AK and the x-axis. Suppose  can be given as a function
can be given as a function 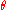 , say
, say 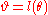 . Let
. Let  be the angle at K so
be the angle at K so 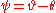 . We can determine r in terms of l using the law of sines. Since
. We can determine r in terms of l using the law of sines. Since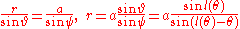 .
.Let P1 and P2 be the points on OK that are distance AK from K, numbering so that
 and
and  .
. 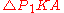 is isosceles with vertex angle
is isosceles with vertex angle 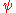 , so the remaining angles,
, so the remaining angles, 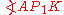 and
and 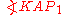 , are
, are 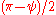 . The angle between AP1 and the x-axis is then
. The angle between AP1 and the x-axis is then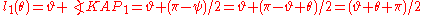 .
.By a similar argument, or simply using the fact that AP1 and AP2 are at right angles, the angle between AP2 and the x-axis is then
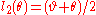 .
.The polar equation for the strophoid can now be derived from l1 and l2 from the formula above:
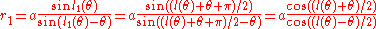

C is a sectrix of Maclaurin with poles O and A when l is of the form
 , in that case l1 and l2 will have the same form so the strophoid is either another sectrix of Maclaurin or a pair of such curves. In this case there is also a simple polar equation for the polar equation if the origin is shifted to the right by a.
, in that case l1 and l2 will have the same form so the strophoid is either another sectrix of Maclaurin or a pair of such curves. In this case there is also a simple polar equation for the polar equation if the origin is shifted to the right by a.Oblique strophoids
Let C be a line through A. Then, in the notation used above,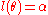 where
where  is a constant. Then
is a constant. Then  and
and  . The polar equations of the resulting strophoid, called an oblique strphoid, with the origin at O are then
. The polar equations of the resulting strophoid, called an oblique strphoid, with the origin at O are then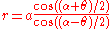
and
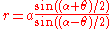 .
.It's easy to check that these equations describe the same curve.
Moving the origin to A (again, see Sectrix of Maclaurin
Sectrix of Maclaurin
In geometry, a sectrix of Maclaurin is defined as the curve swept out by the point of intersection of two lines which are each revolving at constant rates about different points called poles. Equivalently, a sectrix of Maclaurin can be defined as a curve whose equation in biangular coordinates is...
) and replacing −a with a produces
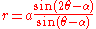 ,
,and rotating by
 in turn produces
in turn produces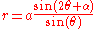 .
.In rectangular coordinates, with a change of constant parameters, this is
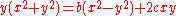 .
.This is a cubic curve and, by the expression in polar coordinates it is rational. It has a crunode
Crunode
A crunode is a point where a curve intersects itself so that both branches of the curve have distinct tangent lines.For a plane curve, defined as the locus of points f = 0, where f is a smooth function of variables x and y ranging over the real numbers, a crunode of the curve is a singularity of...
at (0, 0) and the line y=b is an asymptote.
The right strophoid
Putting in
in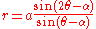
gives
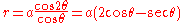 .
.This is called the right strophoid and corresponds to the case where C is the y-axis, O is the origin, and A is the point (a,0).
The Cartesian
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
equation is
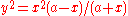 .
.The curve resembles the Folium of Descartes
Folium of Descartes
In geometry, the Folium of Descartes is an algebraic curve defined by the equationx^3 + y^3 - 3 a x y = 0 \,.It forms a loop in the first quadrant with a double point at the origin and asymptotex + y + a = 0 \,.It is symmetrical about y = x....
and the line x = −a is an asymptote
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
to two branches. The curve has two more asymptotes, in the plane with complex coordinates, given by
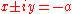 .
.Circles
Let C be a circle through O and A, where O is the origin and A is the point (a, 0). Then, in the notation used above, where
where  is a constant. Then
is a constant. Then  and
and  . The polar equations of the resulting strophoid, called an oblique strphoid, with the origin at O are then
. The polar equations of the resulting strophoid, called an oblique strphoid, with the origin at O are then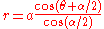
and
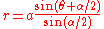 .
.These are the equations of the two circles which also pass through O and A and form angles of
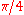 with C at these points.
with C at these points.

