
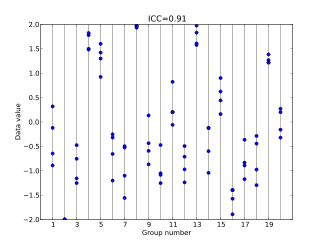
Intraclass correlation
Encyclopedia

Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the intraclass correlation (or the intraclass correlation coefficient, abbreviated ICC) is a descriptive statistic
Descriptive statistics
Descriptive statistics quantitatively describe the main features of a collection of data. Descriptive statistics are distinguished from inferential statistics , in that descriptive statistics aim to summarize a data set, rather than use the data to learn about the population that the data are...
that can be used when quantitative measurements are made on units
Statistical unit
A unit in a statistical analysis refers to one member of a set of entities being studied. It is the material source for the mathematical abstraction of a "random variable"...
that are organized into groups. It describes how strongly units in the same group resemble each other. While it is viewed as a type of correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
, unlike most other correlation measures it operates on data structured as groups, rather than data structured as paired observations.
The intraclass correlation is commonly used to quantify the degree to which individuals with a fixed degree of relatedness (e.g. full siblings) resemble each other in terms of a quantitative trait (see heritability
Heritability
The Heritability of a population is the proportion of observable differences between individuals that is due to genetic differences. Factors including genetics, environment and random chance can all contribute to the variation between individuals in their observable characteristics...
). Another prominent application is the assessment of consistency or reproducibility of quantitative measurements made by different observers measuring the same quantity.
Early definition
The earliest work on intraclass correlations focused on the case of paired measurements, and the first intraclass correlation (ICC) statistics to be proposed were modifications of the interclass correlation (Pearson correlation).Consider a data set consisting of N paired data values (xn,1, xn,2), for n = 1, ..., N. The intraclass correlation r originally proposed by Ronald Fisher
Ronald Fisher
Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...
is
-
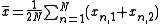 ,
, -
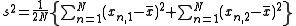 ,
, -
 .
.
Later versions of this statistic used the proper degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
2N −1 in the denominator for calculating s2 and N −1 in the denominator for calculating r, so that s2 becomes unbiased, and r becomes unbiased if s is known.
The key difference between this ICC and the interclass (Pearson) correlation is that the data are pooled to estimate the mean and variance. The reason for this is that in the setting where an intraclass correlation is desired, the pairs are considered to be unordered. For example, if we are studying the resemblance of twins, there is usually no meaningful way to order the values for the two individuals within a twin pair. Like the interclass correlation, the intraclass correlation for paired data will be confined to the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[-1, +1].
The intraclass correlation is also defined for data sets with groups having more than two values. For groups consisting of 3 values, it is defined as
-
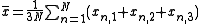 ,
, -
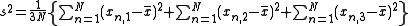 ,
, -
 .
.
As the number of values per groups grows, the number of cross-product terms in this expression grows rapidly. The equivalent form
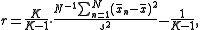
where K is the number of data values per group, and
 is the sample mean of the nth group, is much simpler to calculate.
is the sample mean of the nth group, is much simpler to calculate.This form is usually attributed to Harris
James Arthur Harris
James Arthur Harris was a botanist and biometrician, known for the Benedict-Harris equations,He was the Head of the Department of Botany at the University of Minnesota from 1924 to 1930....
.
The left term is non-negative, consequently the intraclass correlation must satisfy
-
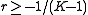 .
.
For large K, this ICC is nearly equal to
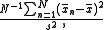
which can be interpreted as the fraction of the total variance that is due to variation between groups.
There is an entire chapter that concerns the intraclass correlation in Ronald Fisher
Ronald Fisher
Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...
's classic book Statistical Methods for Research Workers
Statistical Methods for Research Workers
Statistical Methods for Research Workers is a classic 1925 book on statistics by the statistician R.A. Fisher. It is considered by some to be one of the 20th century's most influential books on statistical methods. According to ,...
.
"Modern" ICCs
Beginning with Ronald Fisher, the intraclass correlation has been regarded within the framework of analysis of varianceAnalysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
(ANOVA), and more recently in the framework of random effects models. A number of ICC estimators have been proposed. Most of the estimators can be defined in terms of the random effects model

where Yij is the jth observation in the ith group, μ is an unobserved overall mean
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
, αi is an unobserved random effect shared by all values in group i, and εij is an unobserved noise term. For the model to be identified, the αi and εij are assumed to have expected value zero and to be uncorrelated with each other. Also, the αi are assumed to be identically distributed, and the εij are assumed to be identically distributed. The variance of αi is denoted σα2 and the variance of εij is denoted σε2.
The population ICC in this framework is
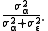
An advantage of the ANOVA framework is that different groups can have different numbers of data values, which is difficult to handle using the earlier ICC statistics. Note also that this ICC is always non-negative, allowing it to be interpreted as the proportion of total variance that is "between groups." This ICC can be generalized to allow for covariate effects, in which case the ICC is interpreted as capturing the within-class similarity of the covariate-adjusted data values.
A number of different ICC statistics have been proposed, not all of which estimate the same population parameter. There has been considerable debate about which ICC statistics are appropriate for a given use, since they may produce markedly different results for the same data.
Relationship to Pearson's correlation coefficient
In terms of its algebraic form, Fisher's original ICC is the ICC that most resembles the Pearson correlation coefficientPearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
. One key difference between the two statistics is that in the ICC, the data are centered and scaled using a pooled mean and standard deviation, whereas in the Pearson correlation, each variable is centered and scaled by its own mean and standard deviation. This pooled scaling for the ICC makes sense because all measurements are of the same quantity (albeit on units in different groups). For example, in a paired data set where each "pair" is a single measurement made for each of two units (e.g., weighing each twin in a pair of identical twins) rather than two different measurements for a single unit (e.g., measuring height and weight for each individual), the ICC is a more natural measure of association than Pearson's correlation.
An important property of the Pearson correlation is that it is invariant to application of separate linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s to the two variables being compared. Thus, if we are correlating X and Y, where, say, Y = 2X + 1, the Pearson correlation between X and Y is 1 — a perfect correlation. This property does not make sense for the ICC, since there is no basis for deciding which transformation is applied to each value in a group. However if all the data in all groups are subjected to the same linear transformation, the ICC does not change.
Use in assessing conformity among observers
The ICC is used to assess the consistency, or conformity, of measurements made by multiple observers measuring the same quantity. For example, if several physicians are asked to score the results of a CT scan for signs of cancer progression, we can ask how consistent the scores are to each other. If the truth is known (for example, if the CT scans were on patients who subsequently underwent exploratory surgery), then the focus would generally be on how well the physicians' scores matched the truth. If the truth is not known, we can only consider the similarity among the scores. An important aspect of this problem is that there is both inter-observer and intra-observer variability. Inter-observer variability refers to systematic differences among the observers — for example, one physician may consistently score patients at a higher risk level than other physicians. Intra-observer variability refers to deviations of a particular observer's score on a particular patient that are not part of a systematic difference.The ICC is constructed to be applied to exchangeable measurements — that is, grouped data in which there is no meaningful way to order the measurements within a group. In assessing conformity among observers, if the same observers rate each element being studied, then systematic differences among observers are likely to exist, which conflicts with the notion of exchangeability. If the ICC is used in a situation where systematic differences exist, the result is a composite measure of intra-observer and inter-observer variability. One situation where exchangeability might reasonably be presumed to hold would be where a specimen to be scored, say a blood specimen, is divided into multiple aliquots, and the aliquots are measured separately on the same instrument. In this case, exchangeability would hold as long as no effect due to the sequence of running the samples was present.
Since the intraclass correlation coefficient gives a composite of intra-observer and inter-observer variability when used with data where the observers are not exchangeable, its results are sometimes considered difficult to interpret in that setting. Alternative measures such as Cohen's kappa statistic, the Fleiss kappa, and the concordance correlation coefficient
Concordance correlation coefficient
In statistics, the concordance correlation coefficient measures the agreement between two variables, e.g., to evaluate reproducibility or for inter-rater reliability.-Definition:...
have been proposed as more suitable measures of agreement among non-exchangeable observers.
Calculation in software packages
ICC is supported by the FreeFree software
Free software, software libre or libre software is software that can be used, studied, and modified without restriction, and which can be copied and redistributed in modified or unmodified form either without restriction, or with restrictions that only ensure that further recipients can also do...
R
R (programming language)
R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
software package (using the icc command with packages 'psy', 'psych' or 'irr'). Non-free software also supports ICC, for instance SPSS
SPSS
SPSS is a computer program used for survey authoring and deployment , data mining , text analytics, statistical analysis, and collaboration and deployment ....
| Shrout and Fleiss convention | Name in SPSS |
|---|---|
| ICC(1,1) | One-way random single measures |
| ICC(1,k) | One-way random average measures |
| ICC(2,1) | Two-way random single measures (Consistency/Absolute agreement) |
| ICC(2,k) | Two-way random average measures (Consistency/Absolute agreement) |
| ICC(3,1) | Two-way mixed single measures (Consistency/Absolute agreement) |
| ICC(3,k) | Two-way mixed average measures (Consistency/Absolute agreement) |

