In-place matrix transposition
Encyclopedia
In-place matrix transposition, also called in-situ matrix transposition, is the problem of transposing
an N×M matrix
in-place in computer memory
, ideally with O(1) (bounded) additional storage, or at most with additional storage much less than NM. Typically, the matrix is assumed to be stored in row-major order
or column-major order (i.e., contiguous rows or columns, respectively, arranged consecutively).
Performing an in-place transpose (in-situ transpose) is most difficult when N ≠ M, i.e. for a non-square (rectangular) matrix, where it involves a complicated permutation
of the data elements, with many cycle
s of length greater than 2. In contrast, for a square matrix (N = M), all of the cycles of are length 1 or 2, and the transpose can be achieved by a simple loop to swap the upper triangle of the matrix with the lower triangle. Further complications arise if one wishes to maximize memory locality in order to improve cache line utilization or to operate out-of-core (where the matrix does not fit into main memory), since transposes inherently involve non-consecutive memory accesses.
The problem of non-square in-place transposition has been studied since at least the late 1950s, and several algorithms are known, including several which attempt to optimize locality for cache, out-of-core, or similar memory-related contexts.
, one can often avoid explicitly transposing a matrix in memory by simply accessing the same data in a different order. For example, software libraries for linear algebra
, such the BLAS
, typically provide options to specify that certain matrices are to be interpreted in transposed order to avoid the necessity of data movement.
However, there remain a number of circumstances in which it is necessary or desirable to physically reorder a matrix in memory to its transposed ordering. For example, with a matrix stored in row-major order
, the rows of the matrix are contiguous in memory and the columns are discontiguous. If repeated operations need to be performed on the columns, for example in a fast Fourier transform
algorithm (e.g. Frigo & Johnson, 2005), transposing the matrix in memory (to make the columns contiguous) may improve performance by increasing memory locality. Since these situations normally coincide with the case of very large matrices (which exceed the cache size), performing the transposition in-place with minimal additional storage becomes desirable.
Also, as a purely mathematical problem, in-place transposition involves a number of interesting number theory
puzzles that have been worked out over the course of several decades.
In row-major format, this would be stored in computer memory as the sequence (0,1,2,3,4,5,6,7), i.e. the two rows stored consecutively. If we transpose this, we obtain the 4×2 matrix:
which is stored in computer memory as the sequence (0,4,1,5,2,6,3,7).
If we number the storage locations 0 to 7, from left to right, then this permutation consists of four cycles:
, (1 2 4), (3 6 5), (7)
That is, the value in position 0 goes to position 0 (a cycle of length 1, no data motion). And the value in position 1 (in the original storage 0,1,2,…) goes to position 2 (in the transposed storage 0,4,1,…), while the value in position 2 (in the original storage 0,1,2,…) goes to position 4 (in the transposed matrix 0,4,1,5,2,…), while position 4 (in the original storage 0,1,2,3,4,…) goes back to position 1 (in the transposed storage 0,4,1,…). Similarly for the values in position 7 and positions (3 6 5).
for all 
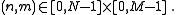
This defines a permutation on the numbers
.
It turns out that one can define simple formulas for P and its inverse (Cate & Twigg, 1977). First:
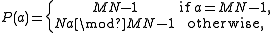
where "mod" is the modulo operation
. Proof: if 0 ≤ a = Mn + m < MN − 1, then Na mod (MN−1) = MN n + Nm mod (MN − 1) = n + Nm.[ Note that MN x mod (MN−1) = (MN − 1) x + x mod (MN−1) = x for 0 ≤ x < MN − 1.] Note that the first (a = 0) and last (a = MN−1) elements are always left invariant under transposition. Second, the inverse permutation is given by:
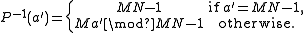
(This is just a consequence of the fact that the inverse of an N×M transpose is an M×N transpose, although it is also easy to show explicitly that P−1 composed with P gives the identity.)
As proved by Cate & Twigg (1977), the number of fixed points
(cycles of length 1) of the permutation is precisely 1 + gcd(N−1,M−1), where gcd is the greatest common divisor
. For example, with N = M the number of fixed points is simply N (the diagonal of the matrix). If N − 1 and M − 1 are coprime
, on the other hand, the only two fixed points are the upper-left and lower-right corners of the matrix.
The number of cycles of any length k>1 is given by (Cate & Twigg, 1977):
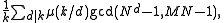
where μ is the Möbius function
and the sum is over the divisor
s d of k.
Furthermore, the cycle containing a=1 (i.e. the second element of the first row of the matrix) is always a cycle of maximum length L, and the lengths k of all other cycles must be divisors of L (Cate & Twigg, 1977).
For a given cycle C, every element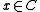
has the same greatest common divisor 
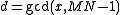. Proof (Brenner, 1973): Let s be the smallest element of the cycle, and 
. From the definition of the permutation P above, every other element x of the cycle is obtained by repeatedly multiplying s by N modulo MN−1, and therefore every other element is divisible by d. But, since N and MN − 1 are coprime, x cannot be divisible by any factor of MN − 1 larger than d, and hence 
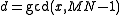. This theorem is useful in searching for cycles of the permutation, since an efficient search can look only at multiples of divisors of MN−1 (Brenner, 1973).
Laflin & Brebner (1970) pointed out that the cycles often come in pairs, which is exploited by several algorithms that permute pairs of cycles at a time. In particular, let s be the smallest element of some cycle C of length k. It follows that MN−1−s is also an element of a cycle of length k (possibly the same cycle). Proof: by the definition of P above, the length k of the cycle containing s is the smallest k > 0 such that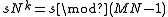
. Clearly, this is the same as the smallest k>0 such that 
, since we are just multiplying both sides by −1, and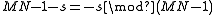 
.
implementing some of these algorithms can be found in the references, below.
to accomplish this (assuming zero-based array indices) is:
for n = 0 to N - 2
for m = n + 1 to N - 1
swap A(n,m) with A(m,n)
This type of implementation, while simple, can exhibit poor performance due to poor cache-line utilization, especially when N is a power of two
(due to cache-line conflicts in a CPU cache
with limited associativity). The reason for this is that, as m is incremented in the inner loop, the memory address corresponding to A(n,m) or A(m,n) jumps discontiguously by N in memory (depending on whether the array is in column-major or row-major format, respectively). That is, the algorithm does not exploit the possibility of spatial locality.
One solution to improve the cache utilization is to "block" the algorithm to operate on several numbers at once, in blocks given by the cache-line size; unfortunately, this means that the algorithm depends on the size of the cache line (it is "cache-aware"), and on a modern computer with multiple levels of cache it requires multiple levels of machine-dependent blocking. Instead, it has been suggested (Frigo et al., 1999) that better performance can be obtained by a recursive
algorithm: divide the matrix into four submatrices of roughly equal size, transposing the two submatrices along the diagonal recursively and transposing and swapping the two submatrices above and below the diagonal. (When N is sufficiently small, the simple algorithm above is used as a base case, as naively recursing all the way down to N=1 would have excessive function-call overhead.) This is a cache-oblivious algorithm, in the sense that it can exploit the cache line without the cache-line size being an explicit parameter.
for each length>1 cycle C of the permutation
pick a starting address s in C
let D = data at s
let x = predecessor of s in the cycle
while x ≠ s
move data from x to successor of x
let x = predecessor of x
move data from D to successor of s
The differences between the algorithms lie mainly in how they locate the cycles, how they find the starting addresses in each cycle, and how they ensure that each cycle is moved exactly once. Typically, as discussed above, the cycles are moved in pairs, since s and MN−1−s are in cycles of the same length (possibly the same cycle). Sometimes, a small scratch array, typically of length M+N (e.g. Brenner, 1973; Cate & Twigg, 1977) is used to keep track of a subset of locations in the array that have been visited, to accelerate the algorithm.
In order to determine whether a given cycle has been moved already, the simplest scheme would be to use O(MN) auxiliary storage, one bit
per element, to indicate whether a given element has been moved. To use only O(M+N) or even O(log MN) auxiliary storage, more complicated algorithms are required, and the known algorithms have a worst-case linearithmic computational cost of O(MN log MN) at best, as first proved by Knuth
(Fich et al., 1995; Gustavson & Swirszcz, 2007).
Such algorithms are designed to move each data element exactly once. However, they also involve a considerable amount of arithmetic to compute the cycles, and require heavily non-consecutive memory accesses since the adjacent elements of the cycles differ by multiplicative factors of N, as discussed above.
architectures optimized for processing consecutive data blocks. The oldest context in which the spatial locality of transposition seems to have been studied is for out-of-core operation (by Alltop, 1975), where the matrix is too large to fit into main memory ("core").
For example, if d = gcd(N,M) is not small, one can perform the transposition using a small amount (NM/d) of additional storage, with at most three passes over the array (Alltop, 1975; Dow, 1995). Two of the passes involve a sequence of separate, small transpositions (which can be performed efficiently out of place using a small buffer) and one involves an in-place d×d square transposition of
blocks (which is efficient since the blocks being moved are large and consecutive, and the cycles are of length at most 2). For the case where |N − M| is small, Dow (1995) describes another algorithm requiring |N − M|⋅min(N,M) additional storage, involving a min(N, M) × min(N, M) square transpose preceded or followed by a small out-of-place transpose. Frigo & Johnson (2005) describe the adaptation of these algorithms to use cache-oblivious techniques for general-purpose CPUs relying on cache lines to exploit spatial locality.
Work on out-of-core matrix transposition, where the matrix does not fit in main memory and must be stored largely on a hard disk
, has focused largely on the N = M square-matrix case, with some exceptions (e.g. Alltop, 1975). Recent reviews of out-of-core algorithms, especially as applied to parallel computing
, can be found in e.g. Suh & Prasanna (2002) and Krishnamoorth et al. (2004).
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
an N×M matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
in-place in computer memory
Computer memory
In computing, memory refers to the physical devices used to store programs or data on a temporary or permanent basis for use in a computer or other digital electronic device. The term primary memory is used for the information in physical systems which are fast In computing, memory refers to the...
, ideally with O(1) (bounded) additional storage, or at most with additional storage much less than NM. Typically, the matrix is assumed to be stored in row-major order
Row-major order
In computing, row-major order and column-major order describe methods for storing multidimensional arrays in linear memory. Following standard matrix notation, rows are numbered by the first index of a two-dimensional array and columns by the second index. Array layout is critical for correctly...
or column-major order (i.e., contiguous rows or columns, respectively, arranged consecutively).
Performing an in-place transpose (in-situ transpose) is most difficult when N ≠ M, i.e. for a non-square (rectangular) matrix, where it involves a complicated permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of the data elements, with many cycle
Cycle (mathematics)
In mathematics, and in particular in group theory, a cycle is a permutation of the elements of some set X which maps the elements of some subset S to each other in a cyclic fashion, while fixing all other elements...
s of length greater than 2. In contrast, for a square matrix (N = M), all of the cycles of are length 1 or 2, and the transpose can be achieved by a simple loop to swap the upper triangle of the matrix with the lower triangle. Further complications arise if one wishes to maximize memory locality in order to improve cache line utilization or to operate out-of-core (where the matrix does not fit into main memory), since transposes inherently involve non-consecutive memory accesses.
The problem of non-square in-place transposition has been studied since at least the late 1950s, and several algorithms are known, including several which attempt to optimize locality for cache, out-of-core, or similar memory-related contexts.
Background
On a computerComputer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
, one can often avoid explicitly transposing a matrix in memory by simply accessing the same data in a different order. For example, software libraries for linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, such the BLAS
Blas
Blas is mainly a Spanish given name and surname, related to Blaise. It may refer to-Places:*Piz Blas, mountain in Switzerland*San Blas , many places - see separate article, also**Cape San Blas Light, lighthouse...
, typically provide options to specify that certain matrices are to be interpreted in transposed order to avoid the necessity of data movement.
However, there remain a number of circumstances in which it is necessary or desirable to physically reorder a matrix in memory to its transposed ordering. For example, with a matrix stored in row-major order
Row-major order
In computing, row-major order and column-major order describe methods for storing multidimensional arrays in linear memory. Following standard matrix notation, rows are numbered by the first index of a two-dimensional array and columns by the second index. Array layout is critical for correctly...
, the rows of the matrix are contiguous in memory and the columns are discontiguous. If repeated operations need to be performed on the columns, for example in a fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
algorithm (e.g. Frigo & Johnson, 2005), transposing the matrix in memory (to make the columns contiguous) may improve performance by increasing memory locality. Since these situations normally coincide with the case of very large matrices (which exceed the cache size), performing the transposition in-place with minimal additional storage becomes desirable.
Also, as a purely mathematical problem, in-place transposition involves a number of interesting number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
puzzles that have been worked out over the course of several decades.
Example
For example, consider the 2×4 matrix:In row-major format, this would be stored in computer memory as the sequence (0,1,2,3,4,5,6,7), i.e. the two rows stored consecutively. If we transpose this, we obtain the 4×2 matrix:
which is stored in computer memory as the sequence (0,4,1,5,2,6,3,7).
If we number the storage locations 0 to 7, from left to right, then this permutation consists of four cycles:
, (1 2 4), (3 6 5), (7)
That is, the value in position 0 goes to position 0 (a cycle of length 1, no data motion). And the value in position 1 (in the original storage 0,1,2,…) goes to position 2 (in the transposed storage 0,4,1,…), while the value in position 2 (in the original storage 0,1,2,…) goes to position 4 (in the transposed matrix 0,4,1,5,2,…), while position 4 (in the original storage 0,1,2,3,4,…) goes back to position 1 (in the transposed storage 0,4,1,…). Similarly for the values in position 7 and positions (3 6 5).
Properties of the permutation
In the following, we assume that the N×M matrix is stored in row-major order with zero-based indices. This means that the (n,m) element, for n = 0,…,N−1 and m = 0,…,M−1, is stored at an address a = Mn + m (plus some offset in memory, which we ignore). In the transposed M×N matrix, the corresponding (m,n) element is stored at the address a' = Nm + n, again in row-major order. 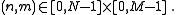We define the transposition permutation to be the function a' = P(a) such that: for all This defines a permutation on the numbers
.It turns out that one can define simple formulas for P and its inverse (Cate & Twigg, 1977). First:
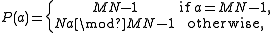
where "mod" is the modulo operation
Modulo operation
In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
. Proof: if 0 ≤ a = Mn + m < MN − 1, then Na mod (MN−1) = MN n + Nm mod (MN − 1) = n + Nm.
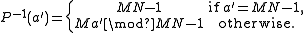
(This is just a consequence of the fact that the inverse of an N×M transpose is an M×N transpose, although it is also easy to show explicitly that P−1 composed with P gives the identity.)
As proved by Cate & Twigg (1977), the number of fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
(cycles of length 1) of the permutation is precisely 1 + gcd(N−1,M−1), where gcd is the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
. For example, with N = M the number of fixed points is simply N (the diagonal of the matrix). If N − 1 and M − 1 are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
, on the other hand, the only two fixed points are the upper-left and lower-right corners of the matrix.
The number of cycles of any length k>1 is given by (Cate & Twigg, 1977):
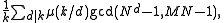
where μ is the Möbius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
and the sum is over the divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s d of k.
Furthermore, the cycle containing a=1 (i.e. the second element of the first row of the matrix) is always a cycle of maximum length L, and the lengths k of all other cycles must be divisors of L (Cate & Twigg, 1977).
For a given cycle C, every element
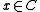has the same greatest common divisor 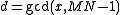. Proof (Brenner, 1973): Let s be the smallest element of the cycle, and . From the definition of the permutation P above, every other element x of the cycle is obtained by repeatedly multiplying s by N modulo MN−1, and therefore every other element is divisible by d. But, since N and MN − 1 are coprime, x cannot be divisible by any factor of MN − 1 larger than d, and hence . 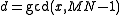This theorem is useful in searching for cycles of the permutation, since an efficient search can look only at multiples of divisors of MN−1 (Brenner, 1973).Laflin & Brebner (1970) pointed out that the cycles often come in pairs, which is exploited by several algorithms that permute pairs of cycles at a time. In particular, let s be the smallest element of some cycle C of length k. It follows that MN−1−s is also an element of a cycle of length k (possibly the same cycle). Proof: by the definition of P above, the length k of the cycle containing s is the smallest k > 0 such that
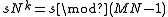. Clearly, this is the same as the smallest k>0 such that , since we are just multiplying both sides by −1, and 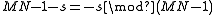.Algorithms
The following briefly summarizes the published algorithms to perform in-place matrix transposition. Source codeSource code
In computer science, source code is text written using the format and syntax of the programming language that it is being written in. Such a language is specially designed to facilitate the work of computer programmers, who specify the actions to be performed by a computer mostly by writing source...
implementing some of these algorithms can be found in the references, below.
Square matrices
For a square N×N matrix An,m = A(n,m), in-place transposition is easy because all of the cycles have length 1 (the diagonals An,n) or length 2 (the upper triangle is swapped with the lower triangle. PseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
to accomplish this (assuming zero-based array indices) is:
for n = 0 to N - 2
for m = n + 1 to N - 1
swap A(n,m) with A(m,n)
This type of implementation, while simple, can exhibit poor performance due to poor cache-line utilization, especially when N is a power of two
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
(due to cache-line conflicts in a CPU cache
CPU cache
A CPU cache is a cache used by the central processing unit of a computer to reduce the average time to access memory. The cache is a smaller, faster memory which stores copies of the data from the most frequently used main memory locations...
with limited associativity). The reason for this is that, as m is incremented in the inner loop, the memory address corresponding to A(n,m) or A(m,n) jumps discontiguously by N in memory (depending on whether the array is in column-major or row-major format, respectively). That is, the algorithm does not exploit the possibility of spatial locality.
One solution to improve the cache utilization is to "block" the algorithm to operate on several numbers at once, in blocks given by the cache-line size; unfortunately, this means that the algorithm depends on the size of the cache line (it is "cache-aware"), and on a modern computer with multiple levels of cache it requires multiple levels of machine-dependent blocking. Instead, it has been suggested (Frigo et al., 1999) that better performance can be obtained by a recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
algorithm: divide the matrix into four submatrices of roughly equal size, transposing the two submatrices along the diagonal recursively and transposing and swapping the two submatrices above and below the diagonal. (When N is sufficiently small, the simple algorithm above is used as a base case, as naively recursing all the way down to N=1 would have excessive function-call overhead.) This is a cache-oblivious algorithm, in the sense that it can exploit the cache line without the cache-line size being an explicit parameter.
Non-square matrices: Following the cycles
For non-square matrices, the algorithms are more complicated. Many of the algorithms prior to 1980 could be described as "follow-the-cycles" algorithms. That is, they loop over the cycles, moving the data from one location to the next in the cycle. In pseudocode form:for each length>1 cycle C of the permutation
pick a starting address s in C
let D = data at s
let x = predecessor of s in the cycle
while x ≠ s
move data from x to successor of x
let x = predecessor of x
move data from D to successor of s
The differences between the algorithms lie mainly in how they locate the cycles, how they find the starting addresses in each cycle, and how they ensure that each cycle is moved exactly once. Typically, as discussed above, the cycles are moved in pairs, since s and MN−1−s are in cycles of the same length (possibly the same cycle). Sometimes, a small scratch array, typically of length M+N (e.g. Brenner, 1973; Cate & Twigg, 1977) is used to keep track of a subset of locations in the array that have been visited, to accelerate the algorithm.
In order to determine whether a given cycle has been moved already, the simplest scheme would be to use O(MN) auxiliary storage, one bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
per element, to indicate whether a given element has been moved. To use only O(M+N) or even O(log MN) auxiliary storage, more complicated algorithms are required, and the known algorithms have a worst-case linearithmic computational cost of O(MN log MN) at best, as first proved by Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
(Fich et al., 1995; Gustavson & Swirszcz, 2007).
Such algorithms are designed to move each data element exactly once. However, they also involve a considerable amount of arithmetic to compute the cycles, and require heavily non-consecutive memory accesses since the adjacent elements of the cycles differ by multiplicative factors of N, as discussed above.
Improving memory locality at the cost of greater total data movement
Several algorithms have been designed to achieve greater memory locality at the cost of greater data movement, as well as slightly greater storage requirements. That is, they may move each data element more than once, but they involve more consecutive memory access (greater spatial locality), which can improve performance on modern CPUs that rely on caches, as well as on SIMDSIMD
Single instruction, multiple data , is a class of parallel computers in Flynn's taxonomy. It describes computers with multiple processing elements that perform the same operation on multiple data simultaneously...
architectures optimized for processing consecutive data blocks. The oldest context in which the spatial locality of transposition seems to have been studied is for out-of-core operation (by Alltop, 1975), where the matrix is too large to fit into main memory ("core").
For example, if d = gcd(N,M) is not small, one can perform the transposition using a small amount (NM/d) of additional storage, with at most three passes over the array (Alltop, 1975; Dow, 1995). Two of the passes involve a sequence of separate, small transpositions (which can be performed efficiently out of place using a small buffer) and one involves an in-place d×d square transposition of
blocks (which is efficient since the blocks being moved are large and consecutive, and the cycles are of length at most 2). For the case where |N − M| is small, Dow (1995) describes another algorithm requiring |N − M|⋅min(N,M) additional storage, involving a min(N, M) × min(N, M) square transpose preceded or followed by a small out-of-place transpose. Frigo & Johnson (2005) describe the adaptation of these algorithms to use cache-oblivious techniques for general-purpose CPUs relying on cache lines to exploit spatial locality.Work on out-of-core matrix transposition, where the matrix does not fit in main memory and must be stored largely on a hard disk
Hard disk
A hard disk drive is a non-volatile, random access digital magnetic data storage device. It features rotating rigid platters on a motor-driven spindle within a protective enclosure. Data is magnetically read from and written to the platter by read/write heads that float on a film of air above the...
, has focused largely on the N = M square-matrix case, with some exceptions (e.g. Alltop, 1975). Recent reviews of out-of-core algorithms, especially as applied to parallel computing
Parallel computing
Parallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...
, can be found in e.g. Suh & Prasanna (2002) and Krishnamoorth et al. (2004).
Source code
- OFFT - recursive block in-place transpose of square matrices, in Fortran
- Jason Stratos Papadopoulos, blocked in-place transpose of square matrices, in CC (programming language)C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
, sci.math.num-analysis newsgroup (April 7, 1998). - See "Source code" links in the references section above, for additional code to perform in-place transposes of both square and non-square matrices.