Yeoh (hyperelastic model)
Encyclopedia
The Yeoh hyperelastic material
Hyperelastic material
A hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic...
model is a phenomenological model for the deformation of nearly incompressible, nonlinear elastic
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
materials such as rubber
Rubber
Natural rubber, also called India rubber or caoutchouc, is an elastomer that was originally derived from latex, a milky colloid produced by some plants. The plants would be ‘tapped’, that is, an incision made into the bark of the tree and the sticky, milk colored latex sap collected and refined...
. The model is based on Ronald Rivlin's
Ronald Rivlin
Ronald Samuel Rivlin was a British-American physicist, mathematician, rheologist and a noted expert on rubber.-Life:Rivlin was born in London in 1915. He studied physics and mathematics at St John's College, Cambridge, being awarded a BA in 1937 and a ScD in 1952...
observation that the elastic properties of rubber may be described using a strain energy density function
Strain energy density function
A strain energy density function or stored energy density function is a scalar valued function that relates the strain energy density of a material to the deformation gradient....
which is a power series in the strain invariants
. The Yeoh model for incompressible rubber is a function only of 
. For compressible rubbers, an dependence on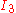 
is added on. Since a polynomial form of the strain energy density function is used but all the three invariants of the left Cauchy-Green deformation tensor are not, the Yeoh model is also called the reduced polynomial modelPolynomial (hyperelastic model)
The polynomial hyperelastic material model is a phenomenological model of rubber elasticity. In this model, the strain energy density function is of the form of a polynomial in the two invariants I_1,I_2 of the left Cauchy-Green deformation tensor....
.
Strain energy density function
The original model proposed by Yeoh had a cubic form with only
dependence and is applicable to purely incompressible materials. The strain energy density for this model is written as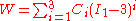
where
are material constants. The quantity 
can be interpreted as the initial shear modulus.Today a slightly more generalized version of the Yeoh model is used. This model includes
terms and is written as
When
the Yeoh model reduces to the neo-Hookean modelNeo-Hookean solid
A Neo-Hookean solid is a hyperelastic material model, similar to Hooke's law, that can be used for predicting the nonlinear stress-strain behavior of materials undergoing large deformations. The model was proposed by Ronald Rivlin in 1948. In contrast to linear elastic materials, a the...
for incompressible materials.
For consistency with linear elasticity
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
the Yeoh model has to satisfy the condition
where
is the shear modulus of the material.Now, at
,
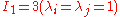Therefore, the consistency condition for the Yeoh model is
Stress-deformation relations
The Cauchy stress for the incompressible Yeoh model is given by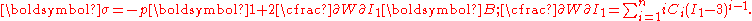
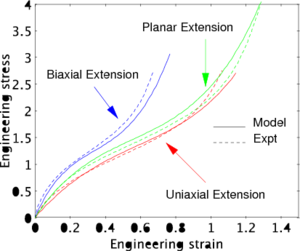
Uniaxial extension
For uniaxial extension in the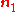
-direction, the principal stretches are 
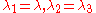. From incompressibility 
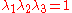. Hence 
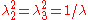.Therefore,
The left Cauchy-Green deformation tensor can then be expressed as
If the directions of the principal stretches are oriented with the coordinate basis vectors, we have
Since
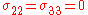, we have
Therefore,
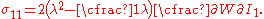
The engineering strain
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is
. The engineering stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is
Equibiaxial extension
For equibiaxial extension in the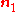
and 
directions, the principal stretches are 
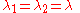. From incompressibility 
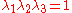. Hence 
.Therefore,
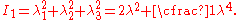
The left Cauchy-Green deformation tensor can then be expressed as
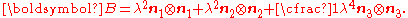
If the directions of the principal stretches are oriented with the coordinate basis vectors, we have
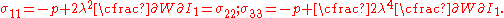
Since
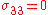, we have
Therefore,
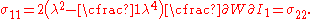
The engineering strain
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is
. The engineering stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is
Planar extension
Planar extension tests are carried out on thin specimens which are constrained from deforming in one direction. For planar extension in the
directions with the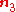 
direction constrained, the principal stretches are 
. From incompressibility 
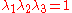. Hence 
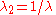.Therefore,
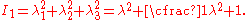
The left Cauchy-Green deformation tensor can then be expressed as
If the directions of the principal stretches are oriented with the coordinate basis vectors, we have
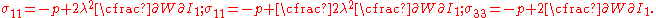
Since
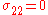, we have
Therefore,
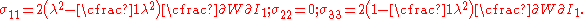
The engineering strain
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is
. The engineering stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is
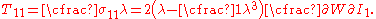
Yeoh model for compressible rubbers
A version of the Yeoh model that includes
dependence is used for compressible rubbers. The strain energy density function for this model is written as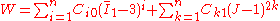
where
, and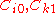 
are material constants. The quantity 
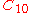is interpreted as half the initial shear modulus, while 
is interpreted as half the initial bulk modulus.When
the compressible Yeoh model reduces to the neo-Hookean modelNeo-Hookean solid
A Neo-Hookean solid is a hyperelastic material model, similar to Hooke's law, that can be used for predicting the nonlinear stress-strain behavior of materials undergoing large deformations. The model was proposed by Ronald Rivlin in 1948. In contrast to linear elastic materials, a the...
for compressible materials.
See also
- Hyperelastic materialHyperelastic materialA hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic...
- Strain energy density functionStrain energy density functionA strain energy density function or stored energy density function is a scalar valued function that relates the strain energy density of a material to the deformation gradient....
- Mooney-Rivlin solid
- Finite strain theory
- Stress measuresStress measuresThe most commonly used measure of stress is the Cauchy stress. However, several other measures of stress can be defined. Some such stress measures that are widely used in continuum mechanics, particularly in the computational context, are:...