The Goldwasser–Micali cryptosystem is an asymmetric key encryption algorithm developed by Shafi Goldwasser

Shafi Goldwasser

Shafrira Goldwasser is the RSA Professor of electrical engineering and computer science at MIT, and a professor of mathematical sciences at the Weizmann Institute of Science, Israel.-Biography:...

 and Silvio Micali

Silvio Micali

Silvio Micali is an Italian-born computer scientist at MIT Computer Science and Artificial Intelligence Laboratory and a professor of computer science in MIT's Department of Electrical Engineering and Computer Science since 1983. His research centers on the theory of cryptography and information...

 in 1982. GM has the distinction of being the first probabilistic

Probabilistic encryption

Probabilistic encryption is the use of randomness in an encryption algorithm, so that when encrypting the same message several times it will, in general, yield different ciphertexts...

 public-key encryption scheme which is provably secure under standard cryptographic assumptions. However, it is not an efficient cryptosystem, as ciphertexts may be several hundred times larger than the initial plaintext. To prove the security properties of the cryptosystem, Goldwasser and Micali proposed the widely-used definition of semantic security

Semantic security

Semantic security is a widely used definition for security in an asymmetric key encryption algorithm. For a cryptosystem to be semantically secure, it must be infeasible for a computationally bounded adversary to derive significant information about a message when given only its ciphertext and...

.

Basis

The GM cryptosystem is semantically secure

Semantic security

Semantic security is a widely used definition for security in an asymmetric key encryption algorithm. For a cryptosystem to be semantically secure, it must be infeasible for a computationally bounded adversary to derive significant information about a message when given only its ciphertext and...

 based on the assumed intractability of the quadratic residuosity problem

Quadratic residuosity problem

The quadratic residuosity problem in computational number theory is the question of distinguishing by calculating the quadratic residues modulo N, where N is a composite number...

 modulo a composite N = pq where p, q are large primes

Prime number

A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...

. This assumption states that given (x, N) it is difficult to determine whether x is a quadratic residue modulo N (i.e., x = y² mod N for some y), when the Jacobi symbol

Jacobi symbol

The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...

 for x is +1. The quadratic residue problem is easily solved given the factorization of N, while new quadratic residues may be generated by any party, even without knowledge of this factorization. The GM cryptosystem leverages this asymmetry by encrypting individual plaintext bits as either random quadratic residues or non-residues modulo N, all with quadratic residue symbol +1. Recipients use the factorization of N as a secret key, and decrypt the message by testing the quadratic residuosity of the received ciphertext values.

Because Goldwasser–Micali produces a value of size approximately |N| to encrypt every single bit of a plaintext, GM encryption results in substantial ciphertext expansion

Ciphertext expansion

In cryptography, the term ciphertext expansion refers to the length increase of a message when it is encrypted. Many modern cryptosystems cause some degree of expansion during the encryption process, for instance when the resulting ciphertext must include a message-unique Initialization Vector...

. To prevent factorization

Factorization

In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...

 attacks, it is recommended that |N| be several hundred bits or more. Thus, the scheme serves mainly as a proof of concept, and more efficient provably-secure schemes such as Elgamal

ElGamal encryption

In cryptography, the ElGamal encryption system is an asymmetric key encryption algorithm for public-key cryptography which is based on the Diffie–Hellman key exchange. It was described by Taher Elgamal in 1984. ElGamal encryption is used in the free GNU Privacy Guard software, recent versions of...

 have been developed since.

Because encryption is performed using a probabilistic algorithm, a given plaintext may produce very different ciphertexts each time it is encrypted. This has significant advantages, as it prevents an adversary from recognizing intercepted messages by comparing them to a dictionary of known ciphertexts.

Scheme definition

Goldwasser–Micali consists of three algorithms: a probabilistic key generation algorithm which produces a public and a private key, a probabilistic encryption algorithm, and a deterministic decryption algorithm.

The scheme relies on deciding whether a given value x is a square mod N, given the factorization (p, q) of N. This can be accomplished using the following procedure:

1. Compute x_p = x mod p, x_q = x mod q.
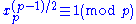2. If and 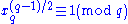, then x is a quadratic residue mod N.

Key generation

The modulus used in GM encryption is generated in the same manner as in the RSA cryptosystem. (See RSA, key generation for details.)

1. Alice generates two distinct large prime number
   Prime number
   A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
   
   s p and q, randomly and independently of each other.
2. Alice computes N = p q.
3. She then finds some non-residue x such that the Legendre symbol
   Legendre symbol
   In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
   
   s satisfy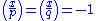 and hence the Jacobi symbol
   Jacobi symbol
   The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
   
     is +1. The value x can for example be found by selecting random values and testing the two Legendre symbols. If (p, q) = 3 mod 4 (i.e., N is a Blum integer
   Blum integer
   In mathematics, a natural number n is a Blum integer if n = p×q is a semiprime for which p and q are distinct prime numbers congruent to 3 mod 4. That is, p and q must be of the form 4t+3, for some integer t. Primes of this form are referred to as Blum primes. This means that the factors of a Blum...
   
   ), then the value N − 1 is guaranteed to have the required property.

The public key consists of (x, N). The secret key is the factorization (p, q).

Message encryption

Suppose Bob wishes to send a message m to Alice:

1. Bob first encodes m as a string of bits (m₁, ..., m_n).
2. For every bit m_i, Bob generates a random value y from the group of units modulo N, or GCD(y,N) = 1. He outputs the value .

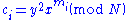Bob sends the ciphertext (c₁, ... , c_n).

Message decryption

Alice receives (c₁, ... , c_n). She can recover m using the following procedure:

1. For each i, using the prime factorization (p, q), Alice determines whether the value c_i is a quadratic residue; if so, m_i = 0, otherwise m_i = 1.

Alice outputs the message m = (m₁, ... , m_n).

Security properties

There is a simple reduction

Reduction (complexity)

In computability theory and computational complexity theory, a reduction is a transformation of one problem into another problem. Depending on the transformation used this can be used to define complexity classes on a set of problems....

 from breaking this cryptosystem to the problem of determining whether a random value modulo N with Jacobi symbol +1 is a quadratic residue. If an algorithm A breaks the cryptosystem,
then to determine if a given value x is a quadratic residue modulo N, we test A to see if it can break the cryptosystem using (x,N) as a public key. If x is a non-residue, then A should work properly. However, if x is a residue, then every "ciphertext" will simply be a random quadratic residue, so
A cannot be correct more than half of the time. Furthermore, this problem is random self-reducible, which ensures that for a given N, every public key is just as secure as every other public key.

The GM cryptosystem has homomorphic properties

Homomorphic encryption

Homomorphic encryption is a form of encryption where a specific algebraic operation performed on the plaintext is equivalent to another algebraic operation performed on the ciphertext. Depending on one's viewpoint, this can be seen as either a positive or negative attribute of the cryptosystem....

, in the sense that if c₀, c₁ are the encryptions of bits m₀, m₁, then c₀c₁ mod N will be an encryption of . For this reason, the GM cryptosystem is sometimes used in more complex cryptographic primitives.