Hodograph
Encyclopedia
A hodograph is a diagram that gives a vectorial visual representation of the movement of a body or a fluid. It is the locus
of one end of a variable vector, with the other end fixed. The position of any plotted data on such a diagram is proportional to the velocity
of the moving particle. It is also called a velocity diagram. It appears to have been used by James Bradley
, but its practical development is mainly from Sir William Rowan Hamilton
, who published an account of it in the Proceedings of the Royal Irish Academy
in 1846.
, astronomy
and fluid mechanics
to plot deformation of material, motion of planet or any other data that involves the velocities of different part of a body.
See Swinging Atwood's machine
In meteorology
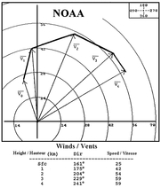
, hodographs are used to plot wind
s from sounding of the Earth's atmosphere
. It is a polar diagram where wind direction is indicated by the angle from the center axis and its strength by the distance from the center. In the figure to the right, at the bottom one finds values of wind at 4 heights above ground. They are plotted by the vectors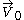
to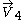 
. One has to notice that direction are plotted as mentioned in the upper right corner.
With the hodograph and thermodynamic diagrams like the tephigram
, meteorologists can calculate:
s into linear version. It consists of interchanging the dependent and independent variables in the equation to achieve linearity.
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of one end of a variable vector, with the other end fixed. The position of any plotted data on such a diagram is proportional to the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the moving particle. It is also called a velocity diagram. It appears to have been used by James Bradley
James Bradley
James Bradley FRS was an English astronomer and served as Astronomer Royal from 1742, succeeding Edmund Halley. He is best known for two fundamental discoveries in astronomy, the aberration of light , and the nutation of the Earth's axis...
, but its practical development is mainly from Sir William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
, who published an account of it in the Proceedings of the Royal Irish Academy
Proceedings of the Royal Irish Academy
The Proceedings of the Royal Irish Academy is the journal of the Royal Irish Academy, founded in 1785 to promote the study of Science, Polite Literature and Antiquities....
in 1846.
Applications
It is used in physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
and fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
to plot deformation of material, motion of planet or any other data that involves the velocities of different part of a body.
See Swinging Atwood's machine
Swinging Atwood's machine
The swinging Atwood's machine is a mechanism that resembles a simple Atwood's machine except that one of the masses is allowed to swing in a two-dimensional plane, producing a dynamical system that is chaotic for some system parameters and initial conditions.Specifically, it comprises two masses ...
Meteorology
Meteorology
Meteorology is the interdisciplinary scientific study of the atmosphere. Studies in the field stretch back millennia, though significant progress in meteorology did not occur until the 18th century. The 19th century saw breakthroughs occur after observing networks developed across several countries...
, hodographs are used to plot wind
Wind
Wind is the flow of gases on a large scale. On Earth, wind consists of the bulk movement of air. In outer space, solar wind is the movement of gases or charged particles from the sun through space, while planetary wind is the outgassing of light chemical elements from a planet's atmosphere into space...
s from sounding of the Earth's atmosphere
Earth's atmosphere
The atmosphere of Earth is a layer of gases surrounding the planet Earth that is retained by Earth's gravity. The atmosphere protects life on Earth by absorbing ultraviolet solar radiation, warming the surface through heat retention , and reducing temperature extremes between day and night...
. It is a polar diagram where wind direction is indicated by the angle from the center axis and its strength by the distance from the center. In the figure to the right, at the bottom one finds values of wind at 4 heights above ground. They are plotted by the vectors
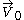to 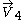. One has to notice that direction are plotted as mentioned in the upper right corner.With the hodograph and thermodynamic diagrams like the tephigram
Tephigram
A tephigram is one of four thermodynamic diagrams commonly used in weather analysis and forecasting. The name evolved from the original name "T-\phi-gram" to describe the axes of temperature and entropy used to create the plot...
, meteorologists can calculate:
- Wind shear: The lines uniting the extremities of successive vectors represent the variation in direction and value of the wind in a layer of the atmosphere. Wind shearWind shearWind shear, sometimes referred to as windshear or wind gradient, is a difference in wind speed and direction over a relatively short distance in the atmosphere...
is important information in the development of thunderstormThunderstormA thunderstorm, also known as an electrical storm, a lightning storm, thundershower or simply a storm is a form of weather characterized by the presence of lightning and its acoustic effect on the Earth's atmosphere known as thunder. The meteorologically assigned cloud type associated with the...
s and future evolution of wind at these levels.
- Turbulence: wind shear indicate the possible turbulenceTurbulenceIn fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
that would cause a hazardHazardA hazard is a situation that poses a level of threat to life, health, property, or environment. Most hazards are dormant or potential, with only a theoretical risk of harm; however, once a hazard becomes "active", it can create an emergency situation. A hazard does not exist when it is not...
to aviationAviationAviation is the design, development, production, operation, and use of aircraft, especially heavier-than-air aircraft. Aviation is derived from avis, the Latin word for bird.-History:...
.
- Temperature advection: change of temperatureTemperatureTemperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
in a layer of air can be calculated by the direction of the wind at that level and the direction of the wind shear with the next level. In the northern hemisphere, warm air is to the right of a wind shear between levels in the atmosphere. The opposite is true in the southern one (see thermal windThermal windThe thermal wind is a vertical shear in the geostrophic wind caused by a horizontal temperature gradient. Its name is a misnomer, because the thermal wind is not actually a wind, but rather a wind shear.- Physical Intuition :...
). So in the example hodograph, the wind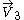
from southwest meet the right side of the wind shear which means a warm advectionAdvectionAdvection, in chemistry, engineering and earth sciences, is a transport mechanism of a substance, or a conserved property, by a fluid, due to the fluid's bulk motion in a particular direction. An example of advection is the transport of pollutants or silt in a river. The motion of the water carries...
and thus warming of the air at that level.
Hodograph transformation
Hodograph transformation is a technique used to transform nonlinear partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s into linear version. It consists of interchanging the dependent and independent variables in the equation to achieve linearity.
Further reading
- Feynman's Lost Lecture: The Motion of Planets Around the SunFeynman's Lost Lecture: The Motion of Planets Around the SunFeynman's Lost Lecture: Motion of Planets Around the Sun is a book based on a lecture by Richard Feynman. Restoration of the lecture notes and conversion into book form was undertaken by Caltech physicist David L. Goodstein and archivist Judith R. Goodstein...
by David L. Goodstein & Judith R. Goodstein (ISBN 0-393-03918-8, W.W.Norton & Company: New York, 1996). In this book the hodograph is used to geometrically derive elliptical (Keplerian) orbits from Newton's laws of motion and gravitation.
See also
- Visual calculusVisual CalculusVisual calculus by Mamikon Mnatsakanian is an approach to solving a variety of integral calculus problems. Many problems that would otherwise seem quite difficult yield to the method with hardly a line of calculation, often reminiscent of what Martin Gardner calls "aha! solutions" or Roger Nelsen...
, a related approach useful in solving a variety of integral calculus problems.
External links
- The Hodograph - Dr. James B. Calvert, University of Denver