
Hidden Field Equations
Encyclopedia
Hidden Fields Equations (HFE) is a public key cryptosystem
which was introduced at Eurocrypt
in 1996 and proposed by Jacques Patarin following the idea of the Matsumoto
and Imai
system. HFE is also known as HFE trapdoor function. It is based on polynomials over finite fields of different size to disguise the relationship between the private key and public key. HFE is in fact a family which consists of basic HFE and combinatorial versions of HFE. The HFE family of cryptosystems is based on the hardness of the problem of finding solutions to a system of multivariate quadratic equations (the so called MQ problem) since it uses private affine transformations to hide the extension field and the private polynomials. Hidden Field Equations also have been used to construct digital signature schemes, e.g. Quartz and Sflash.
of different size to disguise the relationship between the private key and public key. HFE is in fact a family which consists of basic HFE and combinatorial versions of HFE. The HFE family of cryptosystems is based on the hardness of the problem of finding solutions to a system of multivariate quadratic equations (the so called MQ problem) since it uses private affine transformations to hide the extension field and the private polynomials. Hidden Field Equations also have been used to construct digital signature schemes, e.g. Quartz and Sflash.

 over the same base field
over the same base field 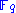 one can interpret a system of
one can interpret a system of  multivariate polynomials in
multivariate polynomials in  variables over
variables over  as a function
as a function  by using a suitable basis
by using a suitable basis
of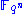 over
over 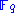 . In almost all applications the polynomials are quadratic, i.e. they have degree 2. We start with the simplest kind of polynomials, namely monomials, and show how they lead to quadratic systems of equations.
. In almost all applications the polynomials are quadratic, i.e. they have degree 2. We start with the simplest kind of polynomials, namely monomials, and show how they lead to quadratic systems of equations.
Let us consider a finite field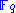 , where
, where 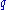 is a power of 2, and an extension field
is a power of 2, and an extension field  . Let
. Let 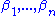 to be a basis
to be a basis
of as an
as an 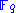 vector space
vector space
. Let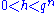 such that
such that 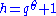 for some
for some 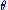 and gcd
and gcd
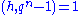 and take a random element
and take a random element  . We represent
. We represent  with respect to the basis as
with respect to the basis as 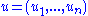 . Define
. Define  by
by
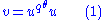
The condition gcd
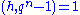 is equivalent to requiring that the map
is equivalent to requiring that the map 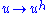 on
on  is one to one and its inverse is the map
is one to one and its inverse is the map 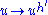 where
where 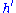 is the multiplicative inverse of
is the multiplicative inverse of  . Choose two secret affine transformation, i.e. two invertible
. Choose two secret affine transformation, i.e. two invertible  matrices
matrices  and
and  with entries in
with entries in 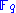 and two vectors
and two vectors 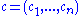 and
and 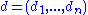 of length
of length  over
over 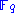 and define
and define  and
and  via:
via:
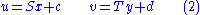
Let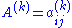 be the matrix of linear transformation in the basis
be the matrix of linear transformation in the basis  such that
such that
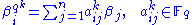
for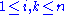 . Write all products of basis elements in terms of the basis, i.e.:
. Write all products of basis elements in terms of the basis, i.e.:

for each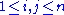 . The system of
. The system of  equations which is explicit in the
equations which is explicit in the 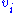 and quadratic in the
and quadratic in the 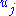 can be obtain by expanding (1) and equating to zero the coefficients of the
can be obtain by expanding (1) and equating to zero the coefficients of the 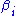 . By using the affine relations in (2) to replace the
. By using the affine relations in (2) to replace the 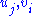 with
with 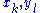 , the system of
, the system of  equations is linear
equations is linear
in the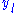 and of degree 2 in the
and of degree 2 in the  . Applying linear algebra
. Applying linear algebra
it will give explicit equations, one for each
explicit equations, one for each  as polynomials of degree 2 in the
as polynomials of degree 2 in the 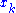 .
.
is to build the secret key starting from a polynomial
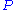 in one unknown
in one unknown  over some finite field
over some finite field
 (normally value
(normally value  is used). This polynomial
is used). This polynomial
can be easily inverted over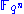 , i.e. it is feasible to find any solutions to the equation
, i.e. it is feasible to find any solutions to the equation 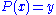 when such solution exist. The secret transformation either decryption and/or signature
when such solution exist. The secret transformation either decryption and/or signature
is based on this inversion. As explained above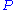 can be identified with a system of
can be identified with a system of  equations
equations  using a fixed basis. To build a cryptosystem
using a fixed basis. To build a cryptosystem
the polynomial
 must be transformed so that the public information hides the original structure and prevents inversion. This is done by viewing the finite fields
must be transformed so that the public information hides the original structure and prevents inversion. This is done by viewing the finite fields 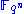 as a vector space
as a vector space
over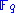 and by choosing two linear affine transformation
and by choosing two linear affine transformation
s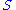 and
and 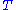 . The triplet
. The triplet  constitute the private key. The private polynomial
constitute the private key. The private polynomial
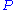 is defined over
is defined over 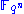 . The public key is
. The public key is  . Below is the diagram for MQ-trapdoor
. Below is the diagram for MQ-trapdoor 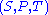 in HFE
in HFE
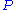 with degree
with degree 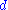 over
over 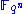 is an element of
is an element of  . If the terms of polynomial
. If the terms of polynomial
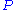 have at most quadratic
have at most quadratic
terms over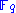 then it will keep the public polynomial small. The case that
then it will keep the public polynomial small. The case that  consists of monomials of the form
consists of monomials of the form 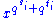 , i.e. with 2 powers of
, i.e. with 2 powers of 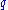 in the exponent
in the exponent
is the basic version of HFE, i.e.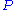 is chosen as
is chosen as
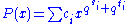
The degree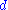 of the polynomial
of the polynomial
is also known as security parameter and the bigger its value the better for security since the resulting set of quadratic equations resembles a randomly chosen set of quadratic equations. On the other side large slows down the deciphering. Since
slows down the deciphering. Since  is a polynomial
is a polynomial
of degree at most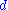 the inverse of
the inverse of 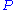 , denoted by
, denoted by 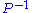 can be computed in
can be computed in 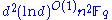 operations.
operations.
 multivariate polynomials
multivariate polynomials  over
over  . It is thus necessary to transfer the message
. It is thus necessary to transfer the message  from
from  in order to encrypt it, i.e. we assume that
in order to encrypt it, i.e. we assume that  is a vector
is a vector 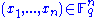 . To encrypt message
. To encrypt message  we evaluate each
we evaluate each 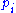 at
at  . The ciphertext is
. The ciphertext is 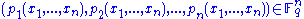 .
.
To understand decryption let us express encryption in terms of . Note that these are not available to the sender. By evaluating the
. Note that these are not available to the sender. By evaluating the 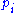 at the message we first apply
at the message we first apply  , resulting in
, resulting in 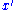 . At this point
. At this point  is transferred from
is transferred from 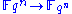 so we can apply the private polynomial
so we can apply the private polynomial 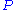 which is over
which is over  and this result is denoted by
and this result is denoted by 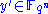 . Once again,
. Once again, 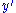 is transferred to the vector
is transferred to the vector  and the transformation
and the transformation 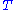 is applied and the final output
is applied and the final output  is produced from
is produced from 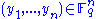 .
.
To decrypt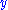 , the above steps are done in reverse order. This is possible if the private key
, the above steps are done in reverse order. This is possible if the private key 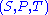 is known. The crucial step in the deciphering is not the inversion of
is known. The crucial step in the deciphering is not the inversion of 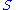 and
and 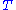 but rather the computations of the solution of
but rather the computations of the solution of 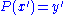 . Since
. Since 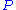 is not necessary a bijection, one may find more than one solution to this inversion (there exist at most d different solutions
is not necessary a bijection, one may find more than one solution to this inversion (there exist at most d different solutions  since
since 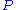 is a polynomial of degree d). The redundancy denoted as
is a polynomial of degree d). The redundancy denoted as  is added at the first step to the message
is added at the first step to the message  in order to select the right
in order to select the right  from the set of solutions
from the set of solutions 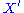 . The diagram below shows the basic HFE for encryption.
. The diagram below shows the basic HFE for encryption.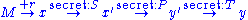
The operations above preserve to some extent the trapdoor solvability of the function.
HFE- and HFEv are very useful in signature schemes as they prevent from slowing down the signature generation and also enhance the overall security of HFE whereas for encryption
both HFE- and HFEv will lead to a rather slow decryption process so neither too many equations can be removed (HFE-) nor too many variables should be added (HFEv). Both HFE- and HFEv were used to obtain Quartz.
For encryption, the situation is better with HFE+ since the decryption process takes the same amount of time, however the public key has more equations than variables.
01. Shamir-Kipnis: Recover the Private Key.
The key point of this attack is to recover the private key as sparse univariate polynomials over the extension field . The attack only works for basic HFE and fails for all its variations.
. The attack only works for basic HFE and fails for all its variations.
02. Faugere: Fast Gröbner Bases.
The idea of Faugere's attacks is to use fast algorithm to compute a Gröbner basis
of the system of polynomial equations. Faugere broke the HFE challenge 1 in 96 hours in 2002 and in 2003 Faugere and Joux worked together on the security of HFE.
Cryptosystem
There are two different meanings of the word cryptosystem. One is used by the cryptographic community, while the other is the meaning understood by the public.- General meaning :...
which was introduced at Eurocrypt
Eurocrypt
Eurocrypt is a conference for cryptography research. The full name of the conference is currently the Annual International Conference on the Theory and Applications of Cryptographic Techniques, but this has not always been its name...
in 1996 and proposed by Jacques Patarin following the idea of the Matsumoto
Matsumoto
Matsumoto is the 16th most common Japanese surname and the name of a city in Nagano Prefecture.-People:* Chizuo Matsumoto, a.k.a...
and Imai
Imai
-People:The Japanese characters link to the Japanese-language Wikipedia*Eriko Imai , artist*Hisae Imai , photographer*Hisashi Imai , Japanese rock musician*Juliana Imai , Brazilian model...
system. HFE is also known as HFE trapdoor function. It is based on polynomials over finite fields
 of different size to disguise the relationship between the private key and public key. HFE is in fact a family which consists of basic HFE and combinatorial versions of HFE. The HFE family of cryptosystems is based on the hardness of the problem of finding solutions to a system of multivariate quadratic equations (the so called MQ problem) since it uses private affine transformations to hide the extension field and the private polynomials. Hidden Field Equations also have been used to construct digital signature schemes, e.g. Quartz and Sflash.
of different size to disguise the relationship between the private key and public key. HFE is in fact a family which consists of basic HFE and combinatorial versions of HFE. The HFE family of cryptosystems is based on the hardness of the problem of finding solutions to a system of multivariate quadratic equations (the so called MQ problem) since it uses private affine transformations to hide the extension field and the private polynomials. Hidden Field Equations also have been used to construct digital signature schemes, e.g. Quartz and Sflash.Mathematical background
One of the central notions to understand how Hidden Field Equations work is to see that for two extension fields
 over the same base field
over the same base field 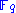 one can interpret a system of
one can interpret a system of  multivariate polynomials in
multivariate polynomials in  variables over
variables over  as a function
as a function  by using a suitable basis
by using a suitable basisBasis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
of
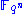 over
over 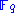 . In almost all applications the polynomials are quadratic, i.e. they have degree 2. We start with the simplest kind of polynomials, namely monomials, and show how they lead to quadratic systems of equations.
. In almost all applications the polynomials are quadratic, i.e. they have degree 2. We start with the simplest kind of polynomials, namely monomials, and show how they lead to quadratic systems of equations.Let us consider a finite field
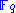 , where
, where 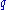 is a power of 2, and an extension field
is a power of 2, and an extension field  . Let
. Let 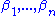 to be a basis
to be a basisBasis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
of
 as an
as an 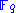 vector space
vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. Let
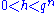 such that
such that 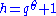 for some
for some 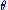 and gcd
and gcdGreatest common divisor of two polynomials
Informally, the greatest common divisor of two polynomials p and q is the largest polynomial that divides both p and q evenly. The definition is modeled on the concept of the greatest common divisor of two integers, the greatest integer that divides both...
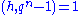 and take a random element
and take a random element  . We represent
. We represent  with respect to the basis as
with respect to the basis as 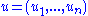 . Define
. Define  by
by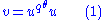
The condition gcd
Greatest common divisor of two polynomials
Informally, the greatest common divisor of two polynomials p and q is the largest polynomial that divides both p and q evenly. The definition is modeled on the concept of the greatest common divisor of two integers, the greatest integer that divides both...
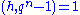 is equivalent to requiring that the map
is equivalent to requiring that the map 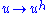 on
on  is one to one and its inverse is the map
is one to one and its inverse is the map 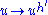 where
where 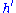 is the multiplicative inverse of
is the multiplicative inverse of  . Choose two secret affine transformation, i.e. two invertible
. Choose two secret affine transformation, i.e. two invertible  matrices
matrices  and
and  with entries in
with entries in 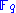 and two vectors
and two vectors 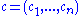 and
and 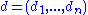 of length
of length  over
over 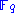 and define
and define  and
and  via:
via: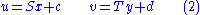
Let
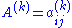 be the matrix of linear transformation in the basis
be the matrix of linear transformation in the basis  such that
such that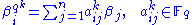
for
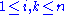 . Write all products of basis elements in terms of the basis, i.e.:
. Write all products of basis elements in terms of the basis, i.e.:
for each
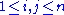 . The system of
. The system of  equations which is explicit in the
equations which is explicit in the 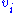 and quadratic in the
and quadratic in the 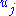 can be obtain by expanding (1) and equating to zero the coefficients of the
can be obtain by expanding (1) and equating to zero the coefficients of the 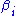 . By using the affine relations in (2) to replace the
. By using the affine relations in (2) to replace the 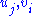 with
with 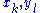 , the system of
, the system of  equations is linear
equations is linearLinear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
in the
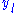 and of degree 2 in the
and of degree 2 in the  . Applying linear algebra
. Applying linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
it will give
 explicit equations, one for each
explicit equations, one for each  as polynomials of degree 2 in the
as polynomials of degree 2 in the 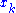 .
.Multivariate cryptosystem
The basic idea of the HFE family of using this as a multivariate cryptosystemCryptosystem
There are two different meanings of the word cryptosystem. One is used by the cryptographic community, while the other is the meaning understood by the public.- General meaning :...
is to build the secret key starting from a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
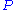 in one unknown
in one unknown  over some finite field
over some finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
 (normally value
(normally value  is used). This polynomial
is used). This polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
can be easily inverted over
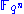 , i.e. it is feasible to find any solutions to the equation
, i.e. it is feasible to find any solutions to the equation 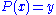 when such solution exist. The secret transformation either decryption and/or signature
when such solution exist. The secret transformation either decryption and/or signatureDigital signature
A digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit...
is based on this inversion. As explained above
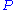 can be identified with a system of
can be identified with a system of  equations
equations  using a fixed basis. To build a cryptosystem
using a fixed basis. To build a cryptosystemCryptosystem
There are two different meanings of the word cryptosystem. One is used by the cryptographic community, while the other is the meaning understood by the public.- General meaning :...
the polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
 must be transformed so that the public information hides the original structure and prevents inversion. This is done by viewing the finite fields
must be transformed so that the public information hides the original structure and prevents inversion. This is done by viewing the finite fields 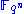 as a vector space
as a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over
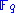 and by choosing two linear affine transformation
and by choosing two linear affine transformationAffine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s
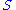 and
and 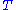 . The triplet
. The triplet  constitute the private key. The private polynomial
constitute the private key. The private polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
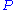 is defined over
is defined over 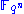 . The public key is
. The public key is  . Below is the diagram for MQ-trapdoor
. Below is the diagram for MQ-trapdoor 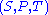 in HFE
in HFE
HFE polynomial
The private polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
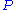 with degree
with degree 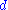 over
over 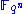 is an element of
is an element of  . If the terms of polynomial
. If the terms of polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
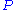 have at most quadratic
have at most quadraticQuadratic
In mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms...
terms over
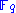 then it will keep the public polynomial small. The case that
then it will keep the public polynomial small. The case that  consists of monomials of the form
consists of monomials of the form 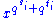 , i.e. with 2 powers of
, i.e. with 2 powers of 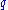 in the exponent
in the exponentis the basic version of HFE, i.e.
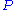 is chosen as
is chosen as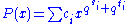
The degree
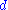 of the polynomial
of the polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
is also known as security parameter and the bigger its value the better for security since the resulting set of quadratic equations resembles a randomly chosen set of quadratic equations. On the other side large
 slows down the deciphering. Since
slows down the deciphering. Since  is a polynomial
is a polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
of degree at most
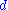 the inverse of
the inverse of 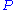 , denoted by
, denoted by 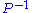 can be computed in
can be computed in 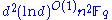 operations.
operations.Encryption and decryption
The public key is given by the multivariate polynomials
multivariate polynomials  over
over  . It is thus necessary to transfer the message
. It is thus necessary to transfer the message  from
from  in order to encrypt it, i.e. we assume that
in order to encrypt it, i.e. we assume that  is a vector
is a vector 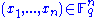 . To encrypt message
. To encrypt message  we evaluate each
we evaluate each 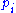 at
at  . The ciphertext is
. The ciphertext is 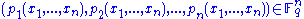 .
.To understand decryption let us express encryption in terms of
 . Note that these are not available to the sender. By evaluating the
. Note that these are not available to the sender. By evaluating the 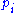 at the message we first apply
at the message we first apply  , resulting in
, resulting in 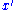 . At this point
. At this point  is transferred from
is transferred from 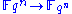 so we can apply the private polynomial
so we can apply the private polynomial 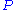 which is over
which is over  and this result is denoted by
and this result is denoted by 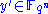 . Once again,
. Once again, 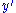 is transferred to the vector
is transferred to the vector  and the transformation
and the transformation 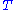 is applied and the final output
is applied and the final output  is produced from
is produced from 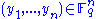 .
.To decrypt
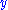 , the above steps are done in reverse order. This is possible if the private key
, the above steps are done in reverse order. This is possible if the private key 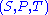 is known. The crucial step in the deciphering is not the inversion of
is known. The crucial step in the deciphering is not the inversion of 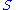 and
and 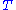 but rather the computations of the solution of
but rather the computations of the solution of 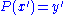 . Since
. Since 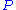 is not necessary a bijection, one may find more than one solution to this inversion (there exist at most d different solutions
is not necessary a bijection, one may find more than one solution to this inversion (there exist at most d different solutions  since
since 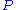 is a polynomial of degree d). The redundancy denoted as
is a polynomial of degree d). The redundancy denoted as  is added at the first step to the message
is added at the first step to the message  in order to select the right
in order to select the right  from the set of solutions
from the set of solutions 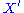 . The diagram below shows the basic HFE for encryption.
. The diagram below shows the basic HFE for encryption.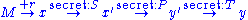
HFE variations
Hidden Field Equations has four basic variations namely +,-,v and f and it is possible to combine them in various way. The basic principle is the following:- 01. The + sign consists of linearity mixing of the public equations with some random equations.
- 02. The - sign is due to Adi Shamir and intends to remove the redundancy 'r' of the public equations.
- 03. The f sign consists of fixing some
 input variables of the public key.
input variables of the public key. - 04. The v sign is defined as a construction and sometimes quite complex such that the inverse of the function can be found only if some v of the variables called vinegar variables are fixed. This idea is due to Jacques Patarin.
The operations above preserve to some extent the trapdoor solvability of the function.
HFE- and HFEv are very useful in signature schemes as they prevent from slowing down the signature generation and also enhance the overall security of HFE whereas for encryption
Encryption
In cryptography, encryption is the process of transforming information using an algorithm to make it unreadable to anyone except those possessing special knowledge, usually referred to as a key. The result of the process is encrypted information...
both HFE- and HFEv will lead to a rather slow decryption process so neither too many equations can be removed (HFE-) nor too many variables should be added (HFEv). Both HFE- and HFEv were used to obtain Quartz.
For encryption, the situation is better with HFE+ since the decryption process takes the same amount of time, however the public key has more equations than variables.
HFE attacks
There are two famous recent attacks on HFE:01. Shamir-Kipnis: Recover the Private Key.
The key point of this attack is to recover the private key as sparse univariate polynomials over the extension field
 . The attack only works for basic HFE and fails for all its variations.
. The attack only works for basic HFE and fails for all its variations.02. Faugere: Fast Gröbner Bases.
The idea of Faugere's attacks is to use fast algorithm to compute a Gröbner basis
Gröbner basis
In computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating subset of an ideal I in a polynomial ring R...
of the system of polynomial equations. Faugere broke the HFE challenge 1 in 96 hours in 2002 and in 2003 Faugere and Joux worked together on the security of HFE.

