Heawood conjecture
Encyclopedia
In graph theory
, the Heawood conjecture or Ringel–Youngs theorem gives a lower bound for the number of colors that are necessary
for graph coloring
on a surface
of a given genus
. It was proven in 1968 by Gerhard Ringel
and John W. T. Youngs. One case, the non-orientable
Klein bottle
, proved an exception to the general formula. An entirely different approach was needed for finding the number of colors needed for the sphere
, eventually solved as the four color theorem
. On the sphere the lower bound is trivial, whereas for higher genera the upper bound is straight forward and was proved in Heawood's original short paper that contained the conjecture.
P.J. Heawood conjecture
d in 1890 that for a given genus g > 0, the minimum number of colors necessary to color all graphs drawn on an orientable surface of that genus (or equivalently to color the regions of any partition of the surface into simply connected regions) is given by
where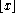
is the floor function
.
Replacing the genus by the Euler characteristic
, we obtain a formula that covers both the orientable and non-orientable cases,
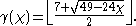
This relation holds, as Ringel and Youngs showed, for all surfaces except for the Klein bottle
. Philip Franklin
(1930) proved that the Klein bottle requires at most 6 colors, rather than 7 as predicted by the formula. The Franklin graph
can be drawn on the Klein bottle in a way that forms six mutually-adjacent regions, showing that this bound is tight.
The upper bound, proved in Heawood's original short paper, is straightforward: by manipulating the Euler characteristic, one can show that any graph embedded in the surface must have at least one vertex of degree less than the given bound. If one removes this vertex, and colors the rest of the graph, the small number of edges incident to the removed vertex ensures that it can be added back to the graph and colored without increasing the needed number of colors beyond the bound. In the other direction, the proof is more difficult, and involves showing that in each case (except the Klein bottle) a complete graph
with a number of vertices equal to the given number of colors can be embedded on the surface.
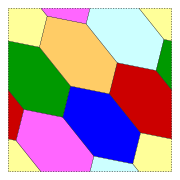The torus
has g = 1, so χ = 0. Therefore, as the formula states, any subdivision of the torus into regions can be colored using at most seven colors. The illustration shows a subdivision of the torus in which each of seven regions are adjacent to each other region; this subdivision shows that the bound of seven on the number of colors is tight for this case. The boundary of this subdivision forms an embedding of the Heawood graph
onto the torus.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Heawood conjecture or Ringel–Youngs theorem gives a lower bound for the number of colors that are necessary
Necessary
Necessary may refer to:help* Something that is a required condition for something else to be the case, see necessary and sufficient condition.* A necessary truth, something that cannot fail to be true, see logical possibility....
for graph coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
on a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
of a given genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
. It was proven in 1968 by Gerhard Ringel
Gerhard Ringel
Gerhard Ringel was a German mathematician who earned his Ph.D. from the University of Bonn in 1951...
and John W. T. Youngs. One case, the non-orientable
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
, proved an exception to the general formula. An entirely different approach was needed for finding the number of colors needed for the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, eventually solved as the four color theorem
Four color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
. On the sphere the lower bound is trivial, whereas for higher genera the upper bound is straight forward and was proved in Heawood's original short paper that contained the conjecture.
Formal statement
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
d in 1890 that for a given genus g > 0, the minimum number of colors necessary to color all graphs drawn on an orientable surface of that genus (or equivalently to color the regions of any partition of the surface into simply connected regions) is given by
where
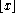is the floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
.
Replacing the genus by the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
, we obtain a formula that covers both the orientable and non-orientable cases,
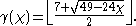
This relation holds, as Ringel and Youngs showed, for all surfaces except for the Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
. Philip Franklin
Philip Franklin
Philip Franklin was an American mathematician and professor whose work was primarily focused in analysis....
(1930) proved that the Klein bottle requires at most 6 colors, rather than 7 as predicted by the formula. The Franklin graph
Franklin graph
In the mathematical field of graph theory, the Franklin graph a 3-regular graph with 12 vertices and 18 edges.The Franklin graph is named after Philip Franklin, who disproved the Heawood conjecture on the number of colors needed when a two-dimensional surface is partitioned into cells by a graph...
can be drawn on the Klein bottle in a way that forms six mutually-adjacent regions, showing that this bound is tight.
The upper bound, proved in Heawood's original short paper, is straightforward: by manipulating the Euler characteristic, one can show that any graph embedded in the surface must have at least one vertex of degree less than the given bound. If one removes this vertex, and colors the rest of the graph, the small number of edges incident to the removed vertex ensures that it can be added back to the graph and colored without increasing the needed number of colors beyond the bound. In the other direction, the proof is more difficult, and involves showing that in each case (except the Klein bottle) a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
with a number of vertices equal to the given number of colors can be embedded on the surface.
Example
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
has g = 1, so χ = 0. Therefore, as the formula states, any subdivision of the torus into regions can be colored using at most seven colors. The illustration shows a subdivision of the torus in which each of seven regions are adjacent to each other region; this subdivision shows that the bound of seven on the number of colors is tight for this case. The boundary of this subdivision forms an embedding of the Heawood graph
Heawood graph
In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.-Combinatorial properties:...
onto the torus.