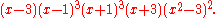In the mathematical

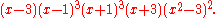
Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 field of graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, the Franklin graph a 3-regular graph

Regular graph

In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...

 with 12 vertices and 18 edges.

The Franklin graph is named after Philip Franklin

Philip Franklin

Philip Franklin was an American mathematician and professor whose work was primarily focused in analysis....

, who disproved the Heawood conjecture

Heawood conjecture

In graph theory, the Heawood conjecture or Ringel–Youngs theorem gives a lower bound for the number of colors that are necessary for graph coloring on a surface of a given genus. It was proven in 1968 by Gerhard Ringel and John W. T. Youngs. One case, the non-orientable Klein bottle, proved an...

 on the number of colors needed when a two-dimensional surface is partitioned into cells by a graph embedding

Graph embedding

In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...

. The Heawood conjecture implied that the maximum chromatic number of a map on the Klein bottle

Klein bottle

In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...

 should be seven, but Franklin proved that in this case six colors always suffice. The Franklin graph can be embedded onto the Klein bottle so that it forms a map requiring six colors, showing that six colors are sometimes necessary in this case.

It is Hamiltonian and has chromatic number 2, chromatic index 3, radius 3, diameter 3 and girth 4. It is also a 3-vertex-connected

K-vertex-connected graph

In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...

 and 3-edge-connected

K-edge-connected graph

In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G =  be an arbitrary graph....

 perfect graph

Perfect graph

In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....

.

Algebraic properties

The automorphism group

Graph automorphism

In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....

 of the Franklin graph is of order 48 and is isomorphic to Z/2Z×S₄, the direct product of the cyclic group

Cyclic group

In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...

 Z/2Z and the symmetric group

Symmetric group

In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...

 S₄. It acts transitively on the vertices of the graph, making it vertex-transitive

Vertex-transitive graph

In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...

.

The characteristic polynomial

Characteristic polynomial

In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....

of the Franklin graph is