Hahn series
Encyclopedia
In mathematics
, Hahn series (sometimes also known as Hahn-Mal'cev-Neumann series) are a type of formal infinite series. They are a generalization of Puiseux series
(themselves a generalization of formal power series
) and were first introduced by Hans Hahn
in 1907 (and then further generalized by Anatoly Maltsev
and Bernhard Neumann
to a non-commutative setting). They allow for arbitrary exponents of the indeterminate
so long as the set supporting them forms a well-ordered subset
of the value group (typically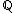
or 
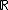). Hahn series were first introduced, as groups, in the course of the proof of the Hahn embedding theorem
and then studied by him as fields in his approach to Hilbert's seventeenth problem
.
(in the indeterminate T) over a field
K and with value group Γ (an ordered group) is the set of formal expressions of the form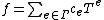
, such that the support 
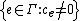of f is well-ordered. The sum and product of 
and 
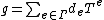are given by 
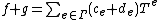and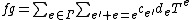 
(in the latter, the sum 
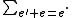over values 
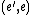such that 
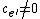and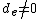 
is finite because a well-ordered set cannot contain an infinite decreasing sequence).
For example,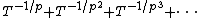
is a Hahn series (over any field) because the set of rationals 
is well-ordered; it is not a Puiseux series because the denominators in the exponents are unbounded. (And if the base field K has characteristic p, then this Hahn series satisfies the equation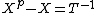 
so it is algebraic over 
.)
The valuation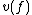
of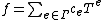 
is defined as the smallest e such that 
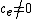(in other words, the smallest element of the support of f): this makes 
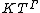into a valued field with value group Γ (justifying a posteriori the terminology). This valuation in turn defines a (translation-invariant) distance
(which is complete and ultrametric), hence a topology
on the field of Hahn series by letting the distance from f to 0 be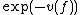
. However, unlike in the case of formal Laurent series or Puiseux series, the formal sums used in defining the elements of the field do not become convergent series for this topology: in the case of 
for example, the norms of the partial sums tend to 1 (because their valuations tend to 0), so the series is not convergent (such series are sometimes known as "pseudo-convergent").
If K is algebraically closed (but not necessarily of characteristic zero) and Γ is divisible, then
is algebraically closed. Thus, the algebraic closure of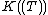 
is contained in 
(when K is of characteristic zero, it is exactly the field of Puiseux series
): in fact, it is possible to give a somewhat analogous description of the algebraic closure of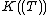
in positive characteristic as a subset of 
.
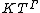If K is an ordered field
then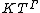
is totally ordered by making the indeterminate T infinitesimal (greater than 0 but less than any positive element of K) or, equivalently, by using the lexicographic order on the coefficients of the series. If K is real-closed
and Γ is divisible then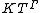
is itself real closed. This fact can be used to analyse (or even construct) the field of surreal number
s (which is isomorphic, as an ordered field, to the field of Hahn series with real coefficients and value group the surreal numbers themselves).
If κ is a infinite regular cardinal
, one can consider the subset of
consisting of series whose support set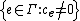 
has cardinality (strictly) less than κ: it turns out that this is also a field, with much the same algebraic closedness properties as the full 
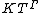: e.g., it is algebraically closed or real closed when K is so and Γ is divisible.
s (at least over a perfect field
) to form “twisted Hahn series” or “Hahn-Witt series”: for example, over a finite field K of characteristic p (or their algebraic closure), the field of Hahn-Witt series with value group Γ (containing the integers) would be the set of formal sums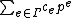
where now 
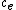are Teichmüller representatives (of the elements of K) which are multiplied and added in the same way as in the case of ordinary Witt vectors (which is obtained when Γ is the group of integers). When Γ is the group of rationals or reals and K is the algebraic closure of the finite field with p elements, this construction gives a (ultra)metrically complete algebraically closed field containing the p-adics, hence a more or less explicit description of the field 
or its spherical completion.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Hahn series (sometimes also known as Hahn-Mal'cev-Neumann series) are a type of formal infinite series. They are a generalization of Puiseux series
Puiseux series
In mathematics, Puiseux series are a generalization of formal power series, first introduced by Isaac Newton in 1676 and rediscovered by Victor Puiseux in 1850, that allows for negative and fractional exponents of the indeterminate...
(themselves a generalization of formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
) and were first introduced by Hans Hahn
Hans Hahn
Hans Hahn was an Austrian mathematician who made contributions to functional analysis, topology, set theory, the calculus of variations, real analysis, and order theory.-Biography:...
in 1907 (and then further generalized by Anatoly Maltsev
Anatoly Maltsev
Anatoly Ivanovich Maltsev was born in Misheronsky, near Moscow, and died in Novosibirsk, USSR. He was a mathematician noted for his work on the decidability of various algebraic groups...
and Bernhard Neumann
Bernhard Neumann
Bernhard Hermann Neumann AC FRS was a German-born British mathematician who was one of the leading figures in group theory, greatly influencing the direction of the subject....
to a non-commutative setting). They allow for arbitrary exponents of the indeterminate
Indeterminate (variable)
In mathematics, and particularly in formal algebra, an indeterminate is a symbol that does not stand for anything else but itself. In particular it does not designate a constant, or a parameter of the problem, it is not an unknown that could be solved for, it is not a variable designating a...
so long as the set supporting them forms a well-ordered subset
Well-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
of the value group (typically
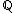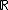or ). Hahn series were first introduced, as groups, in the course of the proof of the Hahn embedding theoremHahn embedding theorem
In mathematics, especially in the area of abstract algebra dealing with ordered structures on abelian groups, the Hahn embedding theorem gives a simple description of all linearly ordered abelian groups....
and then studied by him as fields in his approach to Hilbert's seventeenth problem
Hilbert's seventeenth problem
Hilbert's seventeenth problem is one of the 23 Hilbert problems set out in a celebrated list compiled in 1900 by David Hilbert. It entails expression of definite rational functions as quotients of sums of squares...
.
Formulation
The field of Hahn series (in the indeterminate T) over a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K and with value group Γ (an ordered group) is the set of formal expressions of the form
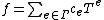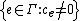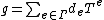, such that the support of f is well-ordered. The sum and product of and are given by 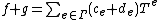and 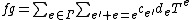(in the latter, the sum 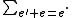over values 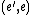such that 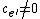and 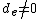is finite because a well-ordered set cannot contain an infinite decreasing sequence).For example,
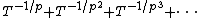is a Hahn series (over any field) because the set of rationals is well-ordered; it is not a Puiseux series because the denominators in the exponents are unbounded. (And if the base field K has characteristic p, then this Hahn series satisfies the equation 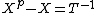so it is algebraic over .)The valuation
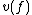of 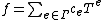is defined as the smallest e such that 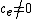(in other words, the smallest element of the support of f): this makes 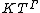into a valued field with value group Γ (justifying a posteriori the terminology). This valuation in turn defines a (translation-invariant) distanceMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
(which is complete and ultrametric), hence a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
on the field of Hahn series by letting the distance from f to 0 be
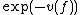. However, unlike in the case of formal Laurent series or Puiseux series, the formal sums used in defining the elements of the field do not become convergent series for this topology: in the case of for example, the norms of the partial sums tend to 1 (because their valuations tend to 0), so the series is not convergent (such series are sometimes known as "pseudo-convergent").If K is algebraically closed (but not necessarily of characteristic zero) and Γ is divisible, then
is algebraically closed. Thus, the algebraic closure of 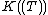is contained in (when K is of characteristic zero, it is exactly the field of Puiseux seriesPuiseux series
In mathematics, Puiseux series are a generalization of formal power series, first introduced by Isaac Newton in 1676 and rediscovered by Victor Puiseux in 1850, that allows for negative and fractional exponents of the indeterminate...
): in fact, it is possible to give a somewhat analogous description of the algebraic closure of
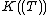in positive characteristic as a subset of 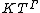.If K is an ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
then
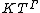is totally ordered by making the indeterminate T infinitesimal (greater than 0 but less than any positive element of K) or, equivalently, by using the lexicographic order on the coefficients of the series. If K is real-closedReal closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
and Γ is divisible then
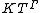is itself real closed. This fact can be used to analyse (or even construct) the field of surreal numberSurreal number
In mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number...
s (which is isomorphic, as an ordered field, to the field of Hahn series with real coefficients and value group the surreal numbers themselves).
If κ is a infinite regular cardinal
Regular cardinal
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
, one can consider the subset of
consisting of series whose support set 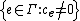has cardinality (strictly) less than κ: it turns out that this is also a field, with much the same algebraic closedness properties as the full 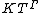: e.g., it is algebraically closed or real closed when K is so and Γ is divisible.Hahn-Witt series
The construction of Hahn series can be combined with Witt vectorWitt vector
In mathematics, a Witt vector is an infinite sequence of elements of a commutative ring. Ernst Witt showed how to put a ring structure on the set of Witt vectors, in such a way that the ring of Witt vectors over the finite field of order p is the ring of p-adic integers.-Motivation:Any p-adic...
s (at least over a perfect field
Separable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
) to form “twisted Hahn series” or “Hahn-Witt series”: for example, over a finite field K of characteristic p (or their algebraic closure), the field of Hahn-Witt series with value group Γ (containing the integers) would be the set of formal sums
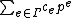where now 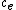are Teichmüller representatives (of the elements of K) which are multiplied and added in the same way as in the case of ordinary Witt vectors (which is obtained when Γ is the group of integers). When Γ is the group of rationals or reals and K is the algebraic closure of the finite field with p elements, this construction gives a (ultra)metrically complete algebraically closed field containing the p-adics, hence a more or less explicit description of the field or its spherical completion.