Ultrametric space
Encyclopedia
In mathematics
, an ultrametric space is a special kind of metric space
in which the triangle inequality
is replaced with d(x, z) ≤ max{d(x, y), d(y, z)}. Sometimes the associated metric is also called a non-Archimedean metric or super-metric. Although some of the theorems for ultrametric spaces may seem strange at a first glance, they appear naturally in many applications.
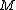with an associated distance function (also called a metric
)
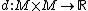
(where R is the set of real number
s), such that for all x, y, z in M, one has:
The last property can be made stronger using the Krull
sharpening to:
For simplicity, let us use the norm
s instead of the distances in the proof; we want to prove that if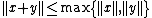
, then the equality occurs if 
. Without loss of generality
, let's assume that
. This implies that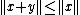 
. But we can also compute 
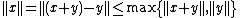. Now, the value of 
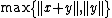cannot be 
, for if that is the case, we have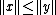 
contrary to the initial assumption. Thus, 
, and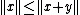 
. Using the initial inequality, we have 
and therefore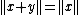 
.
From the above definition, one can conclude several typical properties of ultrametrics. For example, in an ultrametric space, for all x, y, z in M and r, s in R:
In the following, the concept and notation of an (open) ball is the same as in the article about metric space
s, i.e.
Proving these statements is an instructive exercise. Note that, by the second statement, a ball may have several center points that have non-zero distance. The intuition behind such seemingly strange effects is that, due to the strong triangle inequality, distances in ultrametrics do not add up.
may then be thought of as a way of approximating the final result of a computation (which can be guaranteed to exist by the Banach fixed point theorem
). Similar ideas can be found in domain theory
. P-adic analysis
makes heavy use of the ultrametric nature of the p-adic metric.
Applications are also known in solid-state physics, namely in the treatment of spin glasses by the replica-theory of Giorgio Parisi
and coworkers, and also in the theory of aperiodic solids.
Ultrametric distances are also utilized in taxonomy
and phylogenetic tree
construction using the UPGMA
and WPGMA methods.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an ultrametric space is a special kind of metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
in which the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
is replaced with d(x, z) ≤ max{d(x, y), d(y, z)}. Sometimes the associated metric is also called a non-Archimedean metric or super-metric. Although some of the theorems for ultrametric spaces may seem strange at a first glance, they appear naturally in many applications.
Formal definition
Formally, an ultrametric space is a set of points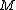 with an associated distance function (also called a metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
)
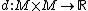
(where R is the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s), such that for all x, y, z in M, one has:
-
-
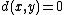iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
-
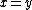
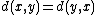(symmetry) -
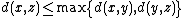(strong triangle or ultrametric inequality).
The last property can be made stronger using the Krull
Wolfgang Krull
Wolfgang Krull was a German mathematician working in the field of commutative algebra.He was born in Baden-Baden, Imperial Germany and died in Bonn, West Germany.- See also :* Krull dimension* Krull topology...
sharpening to:
-
with equality if 
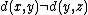
For simplicity, let us use the norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
s instead of the distances in the proof; we want to prove that if
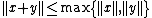, then the equality occurs if . Without loss of generalityWithout loss of generality
Without loss of generality is a frequently used expression in mathematics...
, let's assume that
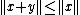. This implies that . But we can also compute 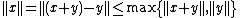. Now, the value of 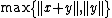cannot be , for if that is the case, we have 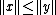contrary to the initial assumption. Thus, , and 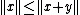. Using the initial inequality, we have and therefore 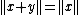.Properties
- Every triangle is isosceles, i.e. d(x,y) = d(y,z) or d(x,z) = d(y,z) or d(x,y) = d(z,x).
In the following, the concept and notation of an (open) ball is the same as in the article about metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s, i.e.
- B(x; r) = { y ∈ M | d(x, y) < r } .
- Every point inside a ball is its center, i.e. if d(x,y) < r then B(x; r) = B(y; r).
- Intersecting balls are contained in each other, i.e. if B(x; r) ∩ B(y; s) is non-empty then either B(x; r) ⊆ B(y; s) or B(y; s) ⊆ B(x; r).
- All balls are both open and closed sets in the induced topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. That is, open balls are also closed, and closed balls (replace < with ≤) are also open. - The set of all open balls with radius r and center in a closed ball of radius r > 0 forms a partitionPartition of a setIn mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the latter, and the mutual distance of two distinct open balls is again equal to r.
Proving these statements is an instructive exercise. Note that, by the second statement, a ball may have several center points that have non-zero distance. The intuition behind such seemingly strange effects is that, due to the strong triangle inequality, distances in ultrametrics do not add up.
Examples
- The discrete metric is an ultrametric.
- Consider the set of wordsFormal languageA formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
of arbitrary length (finite or infinite) over some alphabet Σ. Define the distance between two different words to be 2-n, where n is the first place at which the words differ. The resulting metric is an ultrametric. - The p-adic numbers form a complete ultrametric space.
- If r=(rn) is a sequence of real numbers decreasing to zero, then |x|r := lim supn→∞ |xn|rn induces an ultrametric on the space of all complex sequences for which it is finite. (Note that this is not a seminorm since it lacks homogeneityHomogeneous functionIn mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
. — If the rn are allowed to be zero, one should use here the rather unusual convention that 00=0.) - If G is an edge-weighted undirected graph, all edge weights are positive, and d(u,v) is the weight of the minimax pathWidest path problemIn graph algorithms, the widest path problem, also known as the bottleneck shortest path problem or the maximum capacity path problem, is the problem of finding a path between two designated vertices in a weighted directed graph, maximizing the weight of the minimum-weight edge in the path.For...
between u and v (that is, the largest weight of an edge, on a path chosen to minimize this largest weight), then the vertices of the graph, with distance measured by d, form an ultrametric space, and all finite ultrametric spaces may be represented in this way.
Applications
A contraction mappingContraction mapping
In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...
may then be thought of as a way of approximating the final result of a computation (which can be guaranteed to exist by the Banach fixed point theorem
Banach fixed point theorem
In mathematics, the Banach fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points...
). Similar ideas can be found in domain theory
Domain theory
Domain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
. P-adic analysis
P-adic analysis
In mathematics, p-adic analysis is a branch of number theory that deals with the mathematical analysis of functions of p-adic numbers....
makes heavy use of the ultrametric nature of the p-adic metric.
Applications are also known in solid-state physics, namely in the treatment of spin glasses by the replica-theory of Giorgio Parisi
Giorgio Parisi
Giorgio Parisi is an Italian theoretical physicist. He is best known for his works concerning statistical mechanics, quantum field theory and various aspects of physics, mathematics and science in general....
and coworkers, and also in the theory of aperiodic solids.
Ultrametric distances are also utilized in taxonomy
Taxonomy
Taxonomy is the science of identifying and naming species, and arranging them into a classification. The field of taxonomy, sometimes referred to as "biological taxonomy", revolves around the description and use of taxonomic units, known as taxa...
and phylogenetic tree
Phylogenetic tree
A phylogenetic tree or evolutionary tree is a branching diagram or "tree" showing the inferred evolutionary relationships among various biological species or other entities based upon similarities and differences in their physical and/or genetic characteristics...
construction using the UPGMA
UPGMA
UPGMA is a simple agglomerative or hierarchical clustering method used in bioinformatics for the creation of phenetic trees...
and WPGMA methods.