
Green's function for the three-variable Laplace equation
Encyclopedia
In physics
, the Green's function (or fundamental solution
) for Laplace's equation in three variables is used to describe the response of a particular type of physical system to a point source
. In particular, this Green's function
arises in systems that can be described by Poisson's equation
, a partial differential equation
(PDE) of the form
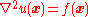
where is the Laplace operator
is the Laplace operator
in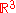 ,
, 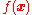 is the source term of the system, and
is the source term of the system, and  is the solution to the equation. Because
is the solution to the equation. Because  is a linear differential operator
is a linear differential operator
, the solution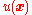 to a general system of this type can be written as an integral over a distribution of source given by
to a general system of this type can be written as an integral over a distribution of source given by 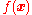 :
:
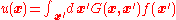
where the Green's function
for Laplace's equation in three variables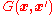 describes the response of the system at the point
describes the response of the system at the point  to a point source located at
to a point source located at 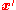 :
:
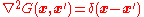
and the point source is given by , the Dirac delta function
, the Dirac delta function
.
. In such a system, the electric field is expressed as the negative gradient of the electric potential
, and Gauss's law
in differential form applies:


Combining these expressions gives
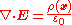 (Poisson's equation
(Poisson's equation
.)
We can find the solution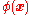 to this equation for an arbitrary charge distribution by temporarily considering the distribution created by a point charge
to this equation for an arbitrary charge distribution by temporarily considering the distribution created by a point charge 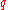 located at
located at 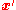 :
:
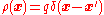
In this case,
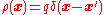
which shows that for
for  will give the response of the system to the point charge
will give the response of the system to the point charge  . Therefore, from the discussion above, if we can find the Green's function of this operator, we can find
. Therefore, from the discussion above, if we can find the Green's function of this operator, we can find 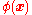 to be
to be
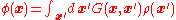
for a general charge distribution.
for Laplace's equation
in three variables is given in terms of the reciprocal distance between two points and is known as the "Newton kernel" or "Newtonian potential
". That is to say, the solution of the equation
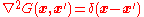
is
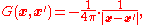
where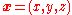 are the standard Cartesian coordinates in a three-dimensional space, and
are the standard Cartesian coordinates in a three-dimensional space, and 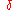 is the Dirac delta function
is the Dirac delta function
.
The algebraic expression of the Green's function for the three-variable Laplace equation, apart from the constant term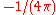 expressed in Cartesian coordinates shall referred to as
expressed in Cartesian coordinates shall referred to as

Many expansion formulas are possible, given the algebraic expression for the Green's function. One of the most well-known of these, the Laplace expansion
for the three-variable Laplace equation, is given in terms of the generating function for Legendre polynomials,
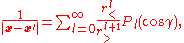
which has been written in terms of spherical coordinates . The less than (greater than) notation means, take the primed or unprimed spherical radius depending on which is less than (greater than) the other. The
. The less than (greater than) notation means, take the primed or unprimed spherical radius depending on which is less than (greater than) the other. The 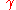 represents the angle between the two arbitrary vectors
represents the angle between the two arbitrary vectors 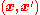 given by
given by

The free-space circular cylindrical Green's function (see below) is given in terms of the reciprocal distance between two points. The expression is derived in Jackson's Classical Electrodynamics text 3rd ed. pages 125–127. Using the Green's function for the three-variable Laplace equation, one can integrate the Poisson equation in order to determine the potential function. Green's functions can be expanded in terms of the basis elements (harmonic functions) which are determined using the separable coordinate systems for the linear partial differential equation. There are many expansions in terms of special functions for the Green's function. In the case of a boundary put at infinity with the boundary condition setting the solution to zero at infinity, then one has an infinite-extent Green's function. For the three-variable Laplace equation, one can for instance expand it in the rotationally invariant coordinate systems which allow separation of variables
. For instance:
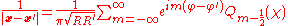
where
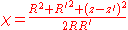
and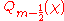 is the odd-half-integer degree Legendre function
is the odd-half-integer degree Legendre function
of the second kind, which is a toroidal harmonic. Here the expansion has been written in terms of cylindrical coordinates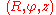 . See for instance Toroidal coordinates
. See for instance Toroidal coordinates
.
Using one of the Whipple formulae
for toroidal harmonics we can obtain an alternative form of the Green's function
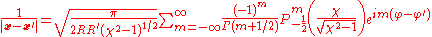
in terms for a toroidal harmonic of the first kind.
This formula was used in 1999 for astrophysical applications in a paper published in The Astrophysical Journal, 527, 86–101, published by Howard Cohl and Joel Tohline. The above-mentioned formula is also known in the engineering community. For instance, a paper written in the Journal of Applied Physics in volume 18, 1947 pages 562-577 shows N.G. De Bruijn and C.J. Boukamp knew of the above relationship. In fact, virtually all the mathematics found in recent papers was already done by Chester Snow. This is found in his book titled Hypergeometric and Legendre Functions with Applications to Integral Equations of Potential Theory, National Bureau of Standards Applied Mathematics Series 19, 1952. Look specifically on pages 228-263. The article by Chester Snow, "Magnetic Fields of Cylindrical Coils and Annular Coils" (National Bureau of Standards, Applied Mathematical Series 38, December 30, 1953), clearly shows the relationship between the free-space Green's function in cylindrical coordinates and the Q-function expression. Likewise, see another one of Snow's pieces of work, titled "Formulas for Computing Capacitance and Inductance", National Bureau of Standards Circular 544, September 10, 1954, pp 13–41. Indeed, not much has been published recently on the subject of toroidal functions and their applications in engineering or physics. However, a number of engineering applications do exist. One application was published; the article was written by J.P. Selvaggi, S. Salon, O. Kwon, and M.V.K. Chari, "Calculating the External Magnetic Field From Permanent Magnets in Permanent-Magnet Motors-An Alternative Method," IEEE Transactions on Magnetics, Vol. 40, No. 5, September 2004. These authors have done extensive work with Legendre functions of the second kind and half-integral degree or toroidal functions of zeroth order. They have solved numerous problems which exhibit circular cylindrical symmetry employing the toroidal functions.
The above expressions for the Green's function for the three-variable Laplace equation are examples of single summation expressions for this Green's function. There are also single-integral expressions for this Green's function. Examples of these can be seen to exist in rotational cylindrical coordinates as an integral Laplace transform in the difference of vertical heights whose kernel is given in terms of the order-zero Bessel function of the first kind as

where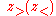 are the greater (lesser) variables
are the greater (lesser) variables  and
and  .
.
Similarly, the Green's function for the three-variable Laplace equation can be given as a Fourier integral cosine transform of the difference of vertical heights whose kernel is given in terms of the order-zero modified Bessel function of the second kind as
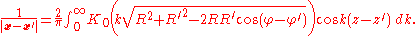
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Green's function (or fundamental solution
Fundamental solution
In mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
) for Laplace's equation in three variables is used to describe the response of a particular type of physical system to a point source
Point source
A point source is a localised, relatively small source of something.Point source may also refer to:*Point source , a localised source of pollution**Point source water pollution, water pollution with a localized source...
. In particular, this Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
arises in systems that can be described by Poisson's equation
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
, a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
(PDE) of the form
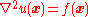
where
 is the Laplace operator
is the Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
in
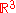 ,
, 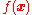 is the source term of the system, and
is the source term of the system, and  is the solution to the equation. Because
is the solution to the equation. Because  is a linear differential operator
is a linear differential operatorDifferential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
, the solution
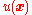 to a general system of this type can be written as an integral over a distribution of source given by
to a general system of this type can be written as an integral over a distribution of source given by 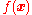 :
: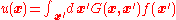
where the Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
for Laplace's equation in three variables
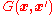 describes the response of the system at the point
describes the response of the system at the point  to a point source located at
to a point source located at 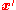 :
: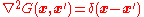
and the point source is given by
 , the Dirac delta function
, the Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
.
Motivation
One physical system of this type is a charge distribution in electrostaticsElectrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
. In such a system, the electric field is expressed as the negative gradient of the electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
, and Gauss's law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
in differential form applies:


Combining these expressions gives
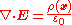 (Poisson's equation
(Poisson's equationPoisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
.)
We can find the solution
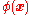 to this equation for an arbitrary charge distribution by temporarily considering the distribution created by a point charge
to this equation for an arbitrary charge distribution by temporarily considering the distribution created by a point charge 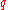 located at
located at 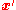 :
: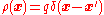
In this case,
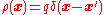
which shows that
 for
for  will give the response of the system to the point charge
will give the response of the system to the point charge  . Therefore, from the discussion above, if we can find the Green's function of this operator, we can find
. Therefore, from the discussion above, if we can find the Green's function of this operator, we can find 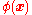 to be
to be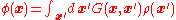
for a general charge distribution.
Mathematical exposition
The free-space Green's functionGreen's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
for Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
in three variables is given in terms of the reciprocal distance between two points and is known as the "Newton kernel" or "Newtonian potential
Newtonian potential
In mathematics, the Newtonian potential or Newton potential is an operator in vector calculus that acts as the inverse to the negative Laplacian, on functions that are smooth and decay rapidly enough at infinity. As such, it is a fundamental object of study in potential theory...
". That is to say, the solution of the equation
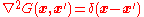
is
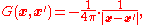
where
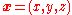 are the standard Cartesian coordinates in a three-dimensional space, and
are the standard Cartesian coordinates in a three-dimensional space, and 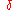 is the Dirac delta function
is the Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
.
The algebraic expression of the Green's function for the three-variable Laplace equation, apart from the constant term
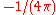 expressed in Cartesian coordinates shall referred to as
expressed in Cartesian coordinates shall referred to as
Many expansion formulas are possible, given the algebraic expression for the Green's function. One of the most well-known of these, the Laplace expansion
Laplace expansion (potential)
In physics, the Laplace expansion of a 1/r - type potential is applied to expand Newton's gravitational potential or Coulomb's electrostatic potential. In quantum mechanical calculations on atoms the expansion is used in the evaluation of integrals of the interelectronic repulsion.The Laplace...
for the three-variable Laplace equation, is given in terms of the generating function for Legendre polynomials,
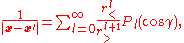
which has been written in terms of spherical coordinates
 . The less than (greater than) notation means, take the primed or unprimed spherical radius depending on which is less than (greater than) the other. The
. The less than (greater than) notation means, take the primed or unprimed spherical radius depending on which is less than (greater than) the other. The 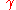 represents the angle between the two arbitrary vectors
represents the angle between the two arbitrary vectors 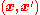 given by
given by
The free-space circular cylindrical Green's function (see below) is given in terms of the reciprocal distance between two points. The expression is derived in Jackson's Classical Electrodynamics text 3rd ed. pages 125–127. Using the Green's function for the three-variable Laplace equation, one can integrate the Poisson equation in order to determine the potential function. Green's functions can be expanded in terms of the basis elements (harmonic functions) which are determined using the separable coordinate systems for the linear partial differential equation. There are many expansions in terms of special functions for the Green's function. In the case of a boundary put at infinity with the boundary condition setting the solution to zero at infinity, then one has an infinite-extent Green's function. For the three-variable Laplace equation, one can for instance expand it in the rotationally invariant coordinate systems which allow separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
. For instance:
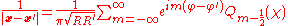
where
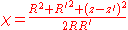
and
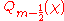 is the odd-half-integer degree Legendre function
is the odd-half-integer degree Legendre functionLegendre function
In mathematics, the Legendre functions Pλ, Qλ and associated Legendre functions P, Q are generalizations of Legendre polynomials to non-integer degree.-Differential equation:...
of the second kind, which is a toroidal harmonic. Here the expansion has been written in terms of cylindrical coordinates
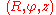 . See for instance Toroidal coordinates
. See for instance Toroidal coordinatesToroidal coordinates
Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci F_1 and F_2 in bipolar coordinates become a ring of radius a in the xy plane of the...
.
Using one of the Whipple formulae
Whipple formulae
In the theory of special functions, Whipple's transformation for Legendre functions, named after Francis John Welsh Whipple, arise from a general expression, concerning associated Legendre functions...
for toroidal harmonics we can obtain an alternative form of the Green's function
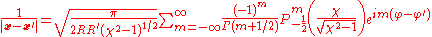
in terms for a toroidal harmonic of the first kind.
This formula was used in 1999 for astrophysical applications in a paper published in The Astrophysical Journal, 527, 86–101, published by Howard Cohl and Joel Tohline. The above-mentioned formula is also known in the engineering community. For instance, a paper written in the Journal of Applied Physics in volume 18, 1947 pages 562-577 shows N.G. De Bruijn and C.J. Boukamp knew of the above relationship. In fact, virtually all the mathematics found in recent papers was already done by Chester Snow. This is found in his book titled Hypergeometric and Legendre Functions with Applications to Integral Equations of Potential Theory, National Bureau of Standards Applied Mathematics Series 19, 1952. Look specifically on pages 228-263. The article by Chester Snow, "Magnetic Fields of Cylindrical Coils and Annular Coils" (National Bureau of Standards, Applied Mathematical Series 38, December 30, 1953), clearly shows the relationship between the free-space Green's function in cylindrical coordinates and the Q-function expression. Likewise, see another one of Snow's pieces of work, titled "Formulas for Computing Capacitance and Inductance", National Bureau of Standards Circular 544, September 10, 1954, pp 13–41. Indeed, not much has been published recently on the subject of toroidal functions and their applications in engineering or physics. However, a number of engineering applications do exist. One application was published; the article was written by J.P. Selvaggi, S. Salon, O. Kwon, and M.V.K. Chari, "Calculating the External Magnetic Field From Permanent Magnets in Permanent-Magnet Motors-An Alternative Method," IEEE Transactions on Magnetics, Vol. 40, No. 5, September 2004. These authors have done extensive work with Legendre functions of the second kind and half-integral degree or toroidal functions of zeroth order. They have solved numerous problems which exhibit circular cylindrical symmetry employing the toroidal functions.
The above expressions for the Green's function for the three-variable Laplace equation are examples of single summation expressions for this Green's function. There are also single-integral expressions for this Green's function. Examples of these can be seen to exist in rotational cylindrical coordinates as an integral Laplace transform in the difference of vertical heights whose kernel is given in terms of the order-zero Bessel function of the first kind as

where
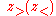 are the greater (lesser) variables
are the greater (lesser) variables  and
and  .
.Similarly, the Green's function for the three-variable Laplace equation can be given as a Fourier integral cosine transform of the difference of vertical heights whose kernel is given in terms of the order-zero modified Bessel function of the second kind as
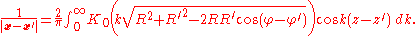
Rotationally invariant Green's functions for the three-variable Laplace equation
Green's function expansions exist in all of the rotationally invariant coordinate systems which are known to yield solutions to the three-variable Laplace equation through the separation of variables technique.See also
- Newtonian potentialNewtonian potentialIn mathematics, the Newtonian potential or Newton potential is an operator in vector calculus that acts as the inverse to the negative Laplacian, on functions that are smooth and decay rapidly enough at infinity. As such, it is a fundamental object of study in potential theory...
- Laplace expansionLaplace expansion (potential)In physics, the Laplace expansion of a 1/r - type potential is applied to expand Newton's gravitational potential or Coulomb's electrostatic potential. In quantum mechanical calculations on atoms the expansion is used in the evaluation of integrals of the interelectronic repulsion.The Laplace...

