
Gompertz curve
Encyclopedia
A Gompertz curve or Gompertz function, named after Benjamin Gompertz
, is a sigmoid function
. It is a type of mathematical model
for a time series
, where growth is slowest at the start and end of a time period. The right-hand or future value asymptote
of the function is approached much more gradually by the curve than the left-hand or lower valued asymptote, in contrast to the logistic function
in which both asymptotes are approached by the curve symmetrically.

where
, which states the rate of mortality (decay) falls exponentially with current size. Mathematically
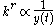
where
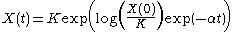
where:
independently on X(0)>0. Note that, in absence of therapies etc.. usually it is X(0)K;
It is easy to verify that the dynamics of X(t) is governed by the Gompertz differential equation:
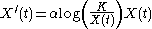
i.e. is of the form:

where F(X) is the instantaneous proliferation rate of the cellular population, whose decreasing nature is due to the competition for the nutrients due to the increase of the cellular population, similarly to the logistic growth rate. However, there is a fundamental difference: in the logistic case the proliferation rate for small cellular population is finite:
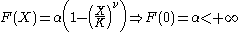
whereas in the Gompertz case the proliferation rate is unbounded:
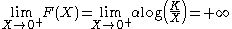
As noticed by Steel and by Wheldon, the proliferation rate of the cellular population is ultimately bounded by the cell division time. Thus, this might be an evidence that the Gompertz equation is not good to model the growth of small tumors. Moreover, more recently it has been noticed that, including the interaction with immune system, Gompertz and other laws characterized by unbounded F(0) would preclude the possibility of immune surveillance.

is the limiting case of the generalized logistic differential equation
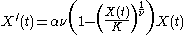
(where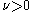 is a positive real number) since
is a positive real number) since
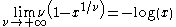 .
.
In addition, there is an inflection point
in the graph of the generalized logistic function
when
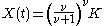
and one in the graph of the Gompertz function when
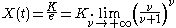 .
.
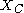 such that for
such that for 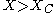 the growth follows the Gompertz Law:
the growth follows the Gompertz Law:
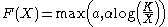
so that:
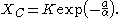
Here there are some numerical estimates for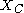 :
:
Benjamin Gompertz
Benjamin Gompertz was a British self educated mathematician and actuary, who became a Fellow of the Royal Society...
, is a sigmoid function
Sigmoid function
Many natural processes, including those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical...
. It is a type of mathematical model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
for a time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
, where growth is slowest at the start and end of a time period. The right-hand or future value asymptote
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
of the function is approached much more gradually by the curve than the left-hand or lower valued asymptote, in contrast to the logistic function
Logistic function
A logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...
in which both asymptotes are approached by the curve symmetrically.
Formula

where
- a is the upper asymptote, since
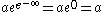
- b, c are negative numbers
- b sets the x displacement
- c sets the growth rate (x scaling)
- e is Euler's NumberE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
(e = 2.71828...)
Differentiation
The function curve can be derived from Gompertz's lawGompertz-Makeham law of mortality
The Gompertz–Makeham lawstates that the death rate is the sum of an age-independent component and an age-dependent component , which increases exponentially with age...
, which states the rate of mortality (decay) falls exponentially with current size. Mathematically
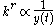
where
-
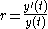 is the rate of growth.
is the rate of growth. - k is an arbitrary constant.
Example uses
Examples of uses for Gompertz curves include:- Mobile phoneMobile phoneA mobile phone is a device which can make and receive telephone calls over a radio link whilst moving around a wide geographic area. It does so by connecting to a cellular network provided by a mobile network operator...
uptake, where costs were initially high (so uptake was slow), followed by a period of rapid growth, followed by a slowing of uptake as saturation was reached. - Population in a confined space, as birth rates first increase and then slow as resource limits are reached.
- Modeling of growth of tumors
Growth of tumors and Gompertz curve
In the sixties A.K. Laird for the first time successfully used the Gompertz curve to fit data of growth of tumors. In fact, tumors are cellular populations growing in a confined space where the availability of nutrients is limited. Denoting the tumor size as X(t) it is useful to write the Gompertz Curve as follows: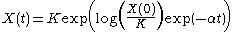
where:
- X(0) is the tumor size at the starting observation time;
- K is the carrying capacity, i.e. the maximum size that can be reached with the available nutrients. In fact it is:
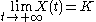
independently on X(0)>0. Note that, in absence of therapies etc.. usually it is X(0)
- α is a constant related to the proliferative ability of the cells.
- log refers to the natural log.
It is easy to verify that the dynamics of X(t) is governed by the Gompertz differential equation:
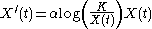
i.e. is of the form:

where F(X) is the instantaneous proliferation rate of the cellular population, whose decreasing nature is due to the competition for the nutrients due to the increase of the cellular population, similarly to the logistic growth rate. However, there is a fundamental difference: in the logistic case the proliferation rate for small cellular population is finite:
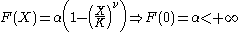
whereas in the Gompertz case the proliferation rate is unbounded:
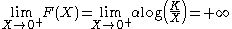
As noticed by Steel and by Wheldon, the proliferation rate of the cellular population is ultimately bounded by the cell division time. Thus, this might be an evidence that the Gompertz equation is not good to model the growth of small tumors. Moreover, more recently it has been noticed that, including the interaction with immune system, Gompertz and other laws characterized by unbounded F(0) would preclude the possibility of immune surveillance.
Gompertz growth and logistic growth
The Gompertz differential equation
is the limiting case of the generalized logistic differential equation
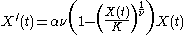
(where
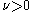 is a positive real number) since
is a positive real number) since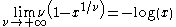 .
.In addition, there is an inflection point
Inflection point
In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
in the graph of the generalized logistic function
Logistic function
A logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...
when
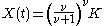
and one in the graph of the Gompertz function when
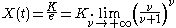 .
.Gomp-ex law of growth
Based on the above considerations, Wheldon proposed a mathematical model of tumor growth, called the Gomp-Ex model, that slightly modifies the Gompertz law. In the Gomp-Ex model it is assumed that initially there is no competition for resources, so that the cellular population expands following the exponential law. However, there is a critical size threshold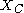 such that for
such that for 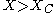 the growth follows the Gompertz Law:
the growth follows the Gompertz Law: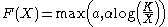
so that:
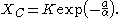
Here there are some numerical estimates for
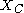 :
:-
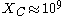 for human tumors
for human tumors -
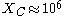 for murine (mouse) tumors
for murine (mouse) tumors
See also
- Logistic functionLogistic functionA logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...
- Gompertz-Makeham law of mortalityGompertz-Makeham law of mortalityThe Gompertz–Makeham lawstates that the death rate is the sum of an age-independent component and an age-dependent component , which increases exponentially with age...
- Growth curveGrowth curveA growth curve is an empirical model of the evolution of a quantity over time. Growth curves are widely used in biology for quantities such as population size, body height or biomass...
- Gompertz distribution

