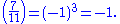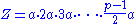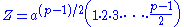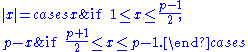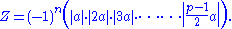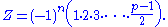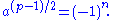Gauss's lemma (number theory)
Encyclopedia
Gauss's lemma in number theory
gives a condition for an integer to be a quadratic residue. Although it is not useful computationally, it has theoretical significance, being involved in some proofs of quadratic reciprocity
.
It made its first appearance in Carl Friedrich Gauss
's third proof (1808) of quadratic reciprocity
and he proved it again in his fifth proof (1818).
to p.
Consider the integers
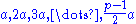
and their least positive residues modulo p. (These residues are all distinct, so there are (p−1)/2 of them.)
Let n be the number of these residues that are greater than p/2. Then
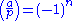
where (a/p) is the Legendre symbol
.
After reduction modulo 11, this sequence becomes
Three of these integers are larger than 11/2 (namely 6, 7 and 10), so n = 3. Correspondingly Gauss's lemma predicts that
This is indeed correct, because 7 is not a quadratic residue modulo 11.
The above sequence of residues
may also be written
In this form, the integers larger than 11/2 appear as negative numbers. It is also apparent that the absolute values of the residues are a permutation of the residues
, can be obtained by evaluating the product
modulo p in two different ways. On one hand it is equal to
The second evaluation takes more work. If x is a nonzero residue modulo p, let us define the "absolute value" of x to be
Since n counts those multiples ka which are in the latter range, and since for those multiples, −ka is in the first range, we have
Now observe that the values |ra| are distinct for r = 1, 2, ..., (p−1)/2. Indeed, if |ra| = |sa|, then ra = ±sa, and therefore r = ±s (because a is invertible modulo p), so r = s because they are both in the range 1 ≤ r ≤ (p−1)/2. But there are exactly (p−1)/2 of them, so they must just be some rearrangement of the integers 1, 2, ..., (p−1)/2. Therefore
Comparing with our first evaluation, we may cancel out the nonzero factor
and we are left with
This is the desired result, because by Euler's criterion
the left hand side is just an alternative expression for the Legendre symbol (a/p).
For example, Eisenstein used Gauss's lemma to prove that if p is an odd prime then
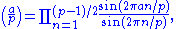
and used this formula to prove quadratic reciprocity, (and, by using elliptic
rather than circular functions, to prove the cubic
and quartic reciprocity
laws.)
Kronecker used the lemma to show that

Switching p and q immediately gives quadratic reciprocity.
It is also used in what are probably the simplest proofs of the "second supplementary law"

and quartic reciprocity
.
with ring of integers
 and let
and let  be a prime ideal. The norm
be a prime ideal. The norm
of is defined as the cardinality of the residue class ring (since
is defined as the cardinality of the residue class ring (since  is prime this is a finite field
is prime this is a finite field
)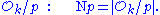
Assume that a primitive nth root of unity
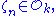 and that n and
and that n and 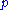 are coprime
are coprime
(i.e. ) Then
) Then
No two distinct nth roots of unity can be congruent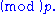
The proof is by contradiction: assume otherwise, that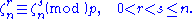 Then letting
Then letting 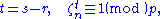 and
and  From the definition of roots of unity,
From the definition of roots of unity,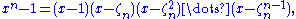 and dividing by x − 1 gives
and dividing by x − 1 gives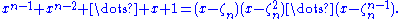
Letting x = 1 and taking residues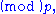

Since n and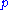 are coprime,
are coprime,  but under the assumption, one of the factors on the right must be zero. Therefore the assumption that two distinct roots are congruent is false.
but under the assumption, one of the factors on the right must be zero. Therefore the assumption that two distinct roots are congruent is false.
Thus the residue classes of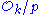 containing the powers of ζn are a subgroup of order n of its (multiplicative) group of units,
containing the powers of ζn are a subgroup of order n of its (multiplicative) group of units, 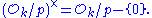 Therefore the order of
Therefore the order of 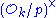 is a multiple of n, and
is a multiple of n, and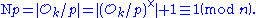
There is an analogue of Fermat's theorem in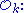 If
If 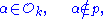 then
then and since
and since 
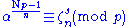 is well-defined and congruent to a unique nth root of unity ζns.
is well-defined and congruent to a unique nth root of unity ζns.
This root of unity is called the nth-power residue symbol for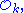 and is denoted by
and is denoted by
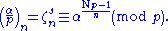
It can be proven that

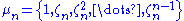 be the multiplicative group of the nth roots of unity, and let
be the multiplicative group of the nth roots of unity, and let  be representatives of the cosets of
be representatives of the cosets of  Then A is called a 1/n system
Then A is called a 1/n system 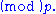
In other words, there are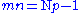 numbers in the set
numbers in the set 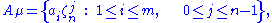 and this set constitutes a representative set for
and this set constitutes a representative set for 
The numbers 1, 2, ..., (p − 1)/2, used in the original version of the lemma, are a 1/2 system (mod p).
Constructing a 1/n system is straightforward: let M be a representative set for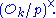 Pick any
Pick any 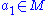 and remove the numbers congruent to
and remove the numbers congruent to 
from M. Pick a2 from M and remove the numbers congruent to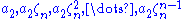 Repeat until M is exhausted. Then {a1, a2, ... am} is a 1/n system
Repeat until M is exhausted. Then {a1, a2, ... am} is a 1/n system 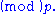
Let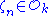 be a primitive nth root of unity,
be a primitive nth root of unity, 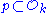 a prime ideal,
a prime ideal, 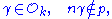 (i.e.
(i.e. 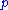 is coprime to both γ and n) and let A = {a1, a2,..., am} be a 1/n system
is coprime to both γ and n) and let A = {a1, a2,..., am} be a 1/n system 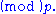
Then for each i, 1 ≤ i ≤ m, there are integers π(i), unique (mod m), and b(i), unique (mod n), such that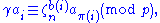
and the nth-power residue symbol is given by the formula
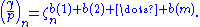
The classical lemma for the quadratic Legendre symbol is the special case n = 2, ζ2 = −1, A = {1, 2, ..., (p − 1)/2}, b(k) = 1 if ak > p/2, b(k) = 0 if ak < p/2.
The existence of the integers π(i) and b(i), and their uniqueness (mod m) and (mod n), respectively, come from the fact that Aμ is a representative set.
Assume that π(i) = π(j) = p, i.e.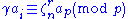 and
and 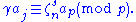
Then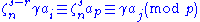
Because γ and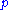 are coprime both sides can be divided by γ, giving
are coprime both sides can be divided by γ, giving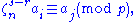
which, since A is a 1/n system, implies s = r and i = j, showing that π is a permutation of the set {1, 2, ..., m}.
Then on the one hand, by the definition of the power residue symbol,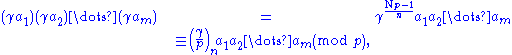
and on the other hand, since π is a permutation,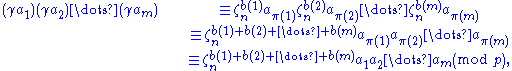
so
and since for all 1 ≤ i ≤ m, ai and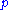 are coprime, a1a2...am can be cancelled from both sides of the congruence,
are coprime, a1a2...am can be cancelled from both sides of the congruence,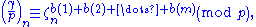
and the theorem follows from the fact that no two distinct nth roots of unity can be congruent (mod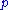 ).
).

Applying the machinery of the transfer
to this collection of coset representatives, we obtain the transfer homomorphism
which turns out to be the map that sends a to (-1)n, where a and n are as in the statement of the lemma. Gauss's lemma may then be viewed as a computation that explicitly identifies this homomorphism as being the quadratic residue character.
and Zolotarev's lemma
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
gives a condition for an integer to be a quadratic residue. Although it is not useful computationally, it has theoretical significance, being involved in some proofs of quadratic reciprocity
Proofs of quadratic reciprocity
In number theory, the law of quadratic reciprocity, like the Pythagorean theorem, has lent itself to an unusual number of proofs. Several hundred proofs of the law of quadratic reciprocity have been found.-Proofs that are accessible:...
.
It made its first appearance in Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
's third proof (1808) of quadratic reciprocity
Quadratic reciprocity
In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
and he proved it again in his fifth proof (1818).
Statement of the lemma
For any odd prime p let a be an integer that is coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to p.
Consider the integers
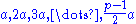
and their least positive residues modulo p. (These residues are all distinct, so there are (p−1)/2 of them.)
Let n be the number of these residues that are greater than p/2. Then
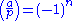
where (a/p) is the Legendre symbol
Legendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
.
Example
Taking p = 11 and a = 7, the relevant sequence of integers is- 7, 14, 21, 28, 35.
After reduction modulo 11, this sequence becomes
- 7, 3, 10, 6, 2.
Three of these integers are larger than 11/2 (namely 6, 7 and 10), so n = 3. Correspondingly Gauss's lemma predicts that
This is indeed correct, because 7 is not a quadratic residue modulo 11.
The above sequence of residues
- 7, 3, 10, 6, 2
may also be written
- -4, 3, -1, -5, 2.
In this form, the integers larger than 11/2 appear as negative numbers. It is also apparent that the absolute values of the residues are a permutation of the residues
- 1, 2, 3, 4, 5.
Proof
A fairly simple proof of the lemma, reminiscent of one of the simplest proofs of Fermat's little theoremProofs of Fermat's little theorem
This article collects together a variety of proofs of Fermat's little theorem, which states thata^p \equiv a \pmod p \,\!for every prime number p and every integer a .-Simplifications:...
, can be obtained by evaluating the product
modulo p in two different ways. On one hand it is equal to
The second evaluation takes more work. If x is a nonzero residue modulo p, let us define the "absolute value" of x to be
Since n counts those multiples ka which are in the latter range, and since for those multiples, −ka is in the first range, we have
Now observe that the values |ra| are distinct for r = 1, 2, ..., (p−1)/2. Indeed, if |ra| = |sa|, then ra = ±sa, and therefore r = ±s (because a is invertible modulo p), so r = s because they are both in the range 1 ≤ r ≤ (p−1)/2. But there are exactly (p−1)/2 of them, so they must just be some rearrangement of the integers 1, 2, ..., (p−1)/2. Therefore
Comparing with our first evaluation, we may cancel out the nonzero factor
and we are left with
This is the desired result, because by Euler's criterion
Euler's criterion
In mathematics, Euler's criterion is used in determining in number theory whether a given integer is a quadratic residue modulo a prime.-Definition:Euler's criterion states:Let p be an odd prime and a an integer coprime to p. Then...
the left hand side is just an alternative expression for the Legendre symbol (a/p).
Applications
Gauss's lemma is used in many, but by no means all, of the known proofs of quadratic reciprocity.For example, Eisenstein used Gauss's lemma to prove that if p is an odd prime then
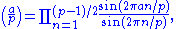
and used this formula to prove quadratic reciprocity, (and, by using elliptic
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
rather than circular functions, to prove the cubic
Cubic reciprocity
Cubic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x3 ≡ p is solvable; the word "reciprocity" comes from the form of the main theorem, which states that if p and q are primary numbers in the...
and quartic reciprocity
Quartic reciprocity
Quartic or biquadratic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x4 ≡ p is solvable; the word "reciprocity" comes from the form of some of these theorems, in that they relate the solvability of the...
laws.)
Kronecker used the lemma to show that

Switching p and q immediately gives quadratic reciprocity.
It is also used in what are probably the simplest proofs of the "second supplementary law"

Higher powers
Generalizations of Gauss's lemma can be used to compute higher power residue symbols. In his second monograph on biquadratic reciprocity, Gauss used a fourth-power lemma to derive the formula for the biquadratic character of 1 + i in Z[i], the ring of Gaussian integers. Subsequently, Eisenstein used third- and fourth-power versions to prove cubicCubic reciprocity
Cubic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x3 ≡ p is solvable; the word "reciprocity" comes from the form of the main theorem, which states that if p and q are primary numbers in the...
and quartic reciprocity
Quartic reciprocity
Quartic or biquadratic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x4 ≡ p is solvable; the word "reciprocity" comes from the form of some of these theorems, in that they relate the solvability of the...
.
nth power residue symbol
Let k be an algebraic number fieldAlgebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
with ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
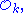 and let
and let  be a prime ideal. The norm
be a prime ideal. The normNorm of an ideal
In commutative algebra, the norm of an ideal is a generalization of a norm of an element in the field extension. It is particularly important in number theory since it measures the size of an ideal of a complicated number ring in terms of an ideal in a less complicated ring...
of
 is defined as the cardinality of the residue class ring (since
is defined as the cardinality of the residue class ring (since 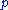 is prime this is a finite field
is prime this is a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
)
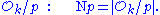
Assume that a primitive nth root of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
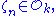 and that n and
and that n and 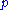 are coprime
are coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
(i.e.
 ) Then
) ThenNo two distinct nth roots of unity can be congruent
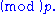
The proof is by contradiction: assume otherwise, that
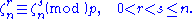 Then letting
Then letting 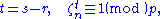 and
and  From the definition of roots of unity,
From the definition of roots of unity,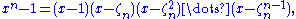 and dividing by x − 1 gives
and dividing by x − 1 gives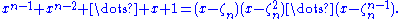
Letting x = 1 and taking residues
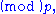

Since n and
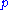 are coprime,
are coprime,  but under the assumption, one of the factors on the right must be zero. Therefore the assumption that two distinct roots are congruent is false.
but under the assumption, one of the factors on the right must be zero. Therefore the assumption that two distinct roots are congruent is false.Thus the residue classes of
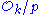 containing the powers of ζn are a subgroup of order n of its (multiplicative) group of units,
containing the powers of ζn are a subgroup of order n of its (multiplicative) group of units, 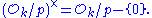 Therefore the order of
Therefore the order of 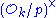 is a multiple of n, and
is a multiple of n, and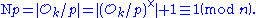
There is an analogue of Fermat's theorem in
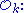 If
If 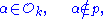 then
then and since
and since 
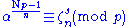 is well-defined and congruent to a unique nth root of unity ζns.
is well-defined and congruent to a unique nth root of unity ζns.This root of unity is called the nth-power residue symbol for
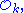 and is denoted by
and is denoted by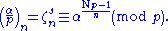
It can be proven that

1/n systems
Let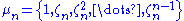 be the multiplicative group of the nth roots of unity, and let
be the multiplicative group of the nth roots of unity, and let  be representatives of the cosets of
be representatives of the cosets of  Then A is called a 1/n system
Then A is called a 1/n system 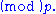
In other words, there are
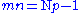 numbers in the set
numbers in the set 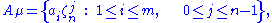 and this set constitutes a representative set for
and this set constitutes a representative set for 
The numbers 1, 2, ..., (p − 1)/2, used in the original version of the lemma, are a 1/2 system (mod p).
Constructing a 1/n system is straightforward: let M be a representative set for
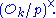 Pick any
Pick any 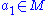 and remove the numbers congruent to
and remove the numbers congruent to 
from M. Pick a2 from M and remove the numbers congruent to
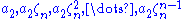 Repeat until M is exhausted. Then {a1, a2, ... am} is a 1/n system
Repeat until M is exhausted. Then {a1, a2, ... am} is a 1/n system 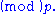
The lemma for nth powers
Gauss's lemma for the nth power residue symbol isLet
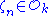 be a primitive nth root of unity,
be a primitive nth root of unity, 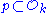 a prime ideal,
a prime ideal, 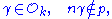 (i.e.
(i.e. 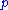 is coprime to both γ and n) and let A = {a1, a2,..., am} be a 1/n system
is coprime to both γ and n) and let A = {a1, a2,..., am} be a 1/n system 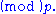
Then for each i, 1 ≤ i ≤ m, there are integers π(i), unique (mod m), and b(i), unique (mod n), such that
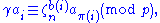
and the nth-power residue symbol is given by the formula
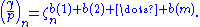
The classical lemma for the quadratic Legendre symbol is the special case n = 2, ζ2 = −1, A = {1, 2, ..., (p − 1)/2}, b(k) = 1 if ak > p/2, b(k) = 0 if ak < p/2.
Proof
The proof of the nth-power lemma uses the same ideas that were used in the proof of the quadratic lemma.The existence of the integers π(i) and b(i), and their uniqueness (mod m) and (mod n), respectively, come from the fact that Aμ is a representative set.
Assume that π(i) = π(j) = p, i.e.
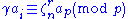 and
and 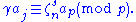
Then
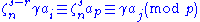
Because γ and
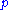 are coprime both sides can be divided by γ, giving
are coprime both sides can be divided by γ, giving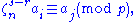
which, since A is a 1/n system, implies s = r and i = j, showing that π is a permutation of the set {1, 2, ..., m}.
Then on the one hand, by the definition of the power residue symbol,
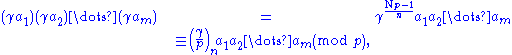
and on the other hand, since π is a permutation,
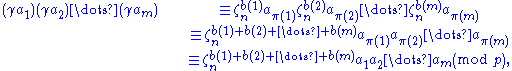
so

and since for all 1 ≤ i ≤ m, ai and
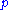 are coprime, a1a2...am can be cancelled from both sides of the congruence,
are coprime, a1a2...am can be cancelled from both sides of the congruence,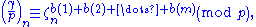
and the theorem follows from the fact that no two distinct nth roots of unity can be congruent (mod
 ).
).Relation to the transfer in group theory
Let G be the multiplicative group of nonzero residue classes in Z/pZ, and let H be the subgroup {+1, −1}. Consider the following coset representatives of H in G,
Applying the machinery of the transfer
Transfer (group theory)
In mathematics, the transfer in group theory is a group homomorphism defined given a group G and a subgroup of finite index H, which goes from the abelianization of G to that of H.-Formulation:...
to this collection of coset representatives, we obtain the transfer homomorphism

which turns out to be the map that sends a to (-1)n, where a and n are as in the statement of the lemma. Gauss's lemma may then be viewed as a computation that explicitly identifies this homomorphism as being the quadratic residue character.
See also
Two other characterizations of squares modulo a prime are Euler's criterionEuler's criterion
In mathematics, Euler's criterion is used in determining in number theory whether a given integer is a quadratic residue modulo a prime.-Definition:Euler's criterion states:Let p be an odd prime and a an integer coprime to p. Then...
and Zolotarev's lemma
Zolotarev's lemma
In number theory, Zolotarev's lemma states that the Legendre symbol\leftfor an integer a modulo an odd prime number p, where p does not divide a, can be computed as the sign of a permutation:...
.