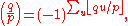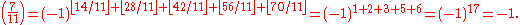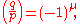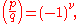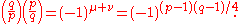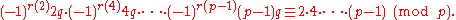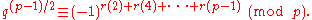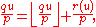
Proofs of quadratic reciprocity
Encyclopedia
In number theory
, the law of quadratic reciprocity
, like the Pythagorean theorem
, has lent itself to an unusual number of proofs
. Several hundred proofs of the law of quadratic reciprocity have been found.
. One by Gotthold Eisenstein counts lattice points. Another applies Zolotarev's lemma
to Z/pqZ expressed by the Chinese remainder theorem
as Z/pZ×Z/qZ, and calculates the signature of a permutation.
The point of departure is "Eisenstein's lemma", which states that for distinct odd primes p, q,
where
denotes the floor function
(the largest integer less than or equal to x), and where the sum is taken over the even integers u = 2, 4, 6, ..., p−1. For example,
This result is very similar to Gauss's lemma
, and can be proved in a similar fashion (proof given below).
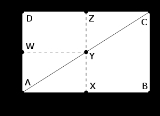
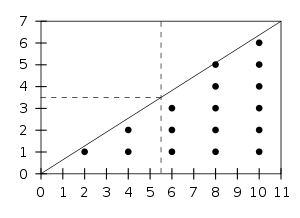
Using this representation of (q/p), the main argument is quite elegant. The sum
counts the number of lattice points with even x-coordinate in the interior of the triangle ABC in the following diagram:
Because each column has an even number of points (namely q−1 points), the number of such lattice points in the region BCYX is the same modulo 2 as the number of such points in the region CZY:
Then by flipping the diagram in both axes, we see that the number of points with even x-coordinate inside CZY is the same as the number of points inside AXY having odd x-coordinates:
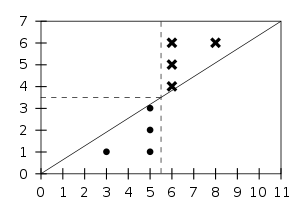The conclusion is that
where μ is the total number of lattice points in the interior of AYX. Switching p and q, the same argument shows that
where ν is the number of lattice points in the interior of WYA. Since there are no lattice points on the line AY itself (because p and q are relatively prime), and since the total number of points in the rectangle WYXA is
we obtain finally
Dividing out successively by 2, 4, ..., p−1 on both sides (which is permissible since none of them are divisible by p) and rearranging, we have
On the other hand, by the definition of r(u) and the floor function,
and so since p is odd and u is even, we see that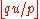
and r(u) are congruent modulo 2. Finally this shows that
We are finished because the left hand side is just an alternative expression for (q/p).
.
where ζp is a primitive pth root of unity
. The basic theory of cyclotomic fields informs us that there is a canonical isomorphism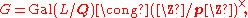
which sends the automorphism σa satisfying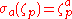
to the element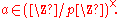
(This is because the morphism of reduction from Z to Z/qZ is injective on the set of p-th roots of unity)
Now consider the subgroup H of squares of elements of G. Since G is cyclic, H has index
2 in G, so the subfield corresponding to H under the Galois correspondence must be a quadratic extension of Q. (In fact it is the unique quadratic extension of Q contained in L.) The Gaussian period
theory determines which one; it turns out to be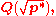
where
At this point we start to see a hint of quadratic reciprocity emerging from our framework. On one hand, the image of H in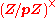
consists precisely of the (nonzero) quadratic residues modulo p. On the other hand, H is related to an attempt to take the square root of p (or possibly of −p). In other words, if now q is an odd prime (different from p), we have so far shown that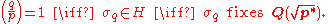
be the Frobenius automorphism associated to β; the characteristic property of
is that
for any x in OL. (The existence of such a Frobenius element depends on quite a bit of algebraic number theory machinery.)
The key fact about
that we need is that for any subfield K of L,
Indeed, let δ be any ideal of OK below β (and hence above q). Then, since
for any x in OK, we see that
is a Frobenius for δ. A standard result concerning
is that its order is equal to the corresponding inertial degree; that is,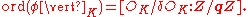
The left hand side is equal to 1 if and only if φ fixes K, and the right hand side is equal to one if and only q splits completely in K, so we are done.
Now, since the pth roots of unity are distinct modulo β (i.e. the polynomial Xp − 1 is separable in characteristic q), we must have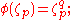
that is,
coincides with the automorphism σq defined earlier. Taking K to be the quadratic field in which we are interested, we obtain the equivalence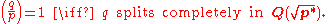
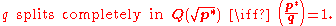
Once we have done this, the law of quadratic reciprocity falls out immediately since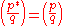
if p = 1 mod 4, and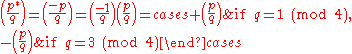
if p = 3 mod 4.
To show the last equivalence, suppose first that
In this case, there is some integer x (not divisible by q) such that
say
for some integer c. Let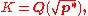
and consider the ideal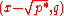
of K. It certainly divides the principal ideal (q). It cannot be equal to (q), since
is not divisible by q. It cannot be the unit ideal, because then
is divisible by q, which is again impossible. Therefore (q) must split in K.
Conversely, suppose that (q) splits, and let β be a prime of K above q. Then
so we may choose some
where a and b are in Q. Actually, since
elementary theory of quadratic fields implies that the ring of integers of K is precisely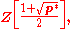
so the denominators of a and b are at worst equal to 2. Since q ≠ 2, we may safely multiply a and b by 2, and assume that
where now a and b are in Z. In this case we have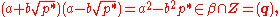
so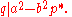
However, q cannot divide b, since then also q divides a, which contradicts our choice of
Therefore, we may divide by b modulo q, to obtain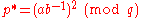
as desired.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the law of quadratic reciprocity
Quadratic reciprocity
In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
, like the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, has lent itself to an unusual number of proofs
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
. Several hundred proofs of the law of quadratic reciprocity have been found.
Proofs that are accessible
Of relatively elementary, combinatorial proofs, there are two which apply types of double countingDouble counting (proof technique)
In combinatorics, double counting, also called counting in two ways, is a combinatorial proof technique for showing that two expressions are equal by demonstrating that they are two ways of counting the size of one set...
. One by Gotthold Eisenstein counts lattice points. Another applies Zolotarev's lemma
Zolotarev's lemma
In number theory, Zolotarev's lemma states that the Legendre symbol\leftfor an integer a modulo an odd prime number p, where p does not divide a, can be computed as the sign of a permutation:...
to Z/pqZ expressed by the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
as Z/pZ×Z/qZ, and calculates the signature of a permutation.
Eisenstein's proof
Eisenstein's proof of quadratic reciprocity is a simplification of Gauss's third proof. It is more geometrically intuitive and requires less technical manipulation.The point of departure is "Eisenstein's lemma", which states that for distinct odd primes p, q,
where
denotes the floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
(the largest integer less than or equal to x), and where the sum is taken over the even integers u = 2, 4, 6, ..., p−1. For example,
This result is very similar to Gauss's lemma
Gauss's lemma (number theory)
Gauss's lemma in number theory gives a condition for an integer to be a quadratic residue. Although it is not useful computationally, it has theoretical significance, being involved in some proofs of quadratic reciprocity....
, and can be proved in a similar fashion (proof given below).
Using this representation of (q/p), the main argument is quite elegant. The sum
counts the number of lattice points with even x-coordinate in the interior of the triangle ABC in the following diagram:  |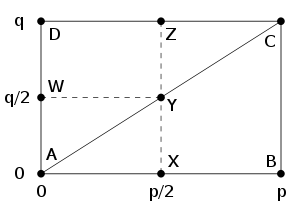
 |
Because each column has an even number of points (namely q−1 points), the number of such lattice points in the region BCYX is the same modulo 2 as the number of such points in the region CZY:
where μ is the total number of lattice points in the interior of AYX. Switching p and q, the same argument shows that
where ν is the number of lattice points in the interior of WYA. Since there are no lattice points on the line AY itself (because p and q are relatively prime), and since the total number of points in the rectangle WYXA is
we obtain finally
Proof of Eisenstein's lemma
For an even integer u in the range 1 ≤ u ≤ p−1, denote by r(u) the least positive residue of qu modulo p. (For example, for p = 11, q = 7, we allow u = 2, 4, 6, 8, 10, and the corresponding values of r(u) are 3, 6, 9, 1, 4.) The numbers (−1)r(u)r(u), again treated as least positive residues modulo p, are all even (in our running example, they are 8, 6, 2, 10, 4.) Furthermore, they are all distinct, because if (−1)r(u)r(u) ≡ (−1)r(t)r(t) mod p, then we may divide out by q to obtain u ≡ ±t mod p. This forces u ≡ t mod p, because both u and t are even, whereas p is odd. Since there exactly (p−1)/2 of them and they are distinct, they must be simply a rearrangement of the even integers 2, 4, ..., p−1. Multiplying them together, we obtain
Dividing out successively by 2, 4, ..., p−1 on both sides (which is permissible since none of them are divisible by p) and rearranging, we have
On the other hand, by the definition of r(u) and the floor function,
and so since p is odd and u is even, we see that
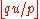and r(u) are congruent modulo 2. Finally this shows that
We are finished because the left hand side is just an alternative expression for (q/p).
Proof using algebraic number theory
The proof presented here is by no means the simplest known; however, it is quite a deep one, in the sense that it motivates some of the ideas of Artin reciprocityArtin reciprocity
The Artin reciprocity law, established by Emil Artin in a series of papers , is a general theorem in number theory that forms a central part of the global class field theory...
.
Cyclotomic field setup
Suppose that p is an odd prime. The action takes place inside the cyclotomic fieldCyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
where ζp is a primitive pth root of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
. The basic theory of cyclotomic fields informs us that there is a canonical isomorphism
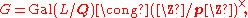
which sends the automorphism σa satisfying
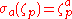
to the element
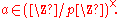
(This is because the morphism of reduction from Z to Z/qZ is injective on the set of p-th roots of unity)
Now consider the subgroup H of squares of elements of G. Since G is cyclic, H has index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2 in G, so the subfield corresponding to H under the Galois correspondence must be a quadratic extension of Q. (In fact it is the unique quadratic extension of Q contained in L.) The Gaussian period
Gaussian period
In mathematics, in the area of number theory, a Gaussian period is a certain kind of sum of roots of unity. The periods permit explicit calculations in cyclotomic fields connected with Galois theory and with harmonic analysis . They are basic in the classical theory called cyclotomy...
theory determines which one; it turns out to be
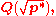
where
At this point we start to see a hint of quadratic reciprocity emerging from our framework. On one hand, the image of H in
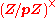
consists precisely of the (nonzero) quadratic residues modulo p. On the other hand, H is related to an attempt to take the square root of p (or possibly of −p). In other words, if now q is an odd prime (different from p), we have so far shown that
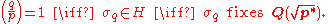
The Frobenius automorphism
Choose any prime ideal β of the ring of integers OL lying over q, which is unramified, and letbe the Frobenius automorphism associated to β; the characteristic property of
is thatfor any x in OL. (The existence of such a Frobenius element depends on quite a bit of algebraic number theory machinery.)
The key fact about
that we need is that for any subfield K of L,Indeed, let δ be any ideal of OK below β (and hence above q). Then, since
for any x in OK, we see that
is a Frobenius for δ. A standard result concerning
is that its order is equal to the corresponding inertial degree; that is,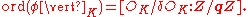The left hand side is equal to 1 if and only if φ fixes K, and the right hand side is equal to one if and only q splits completely in K, so we are done.
Now, since the pth roots of unity are distinct modulo β (i.e. the polynomial Xp − 1 is separable in characteristic q), we must have
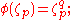
that is,
coincides with the automorphism σq defined earlier. Taking K to be the quadratic field in which we are interested, we obtain the equivalence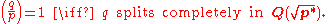Completing the proof
Finally we must show that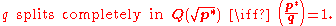Once we have done this, the law of quadratic reciprocity falls out immediately since
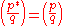
if p = 1 mod 4, and
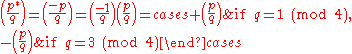
if p = 3 mod 4.
To show the last equivalence, suppose first that
In this case, there is some integer x (not divisible by q) such that
say
for some integer c. Let
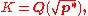
and consider the ideal
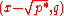
of K. It certainly divides the principal ideal (q). It cannot be equal to (q), since
is not divisible by q. It cannot be the unit ideal, because then
is divisible by q, which is again impossible. Therefore (q) must split in K.
Conversely, suppose that (q) splits, and let β be a prime of K above q. Then
so we may choose some
where a and b are in Q. Actually, since
elementary theory of quadratic fields implies that the ring of integers of K is precisely
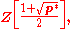
so the denominators of a and b are at worst equal to 2. Since q ≠ 2, we may safely multiply a and b by 2, and assume that
where now a and b are in Z. In this case we have
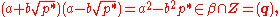
so
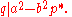
However, q cannot divide b, since then also q divides a, which contradicts our choice of
Therefore, we may divide by b modulo q, to obtain
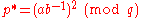
as desired.
External links
- Chronology of Proofs of the Quadratic Reciprocity Law (233 proofs!)