.gif)
G2 (mathematics)
Encyclopedia
In mathematics
, G2 is the name of three simple Lie group
s (a complex form, a compact real form and a split real form), their Lie algebra
s , as well as some algebraic group
, as well as some algebraic group
s. They are the smallest of the five exceptional simple Lie group
s. G2 has rank 2 and dimension 14. Its fundamental representation
is 7-dimensional.
The compact form of G2 can be described as the automorphism group of the octonion algebra
or, equivalently, as the subgroup of that preserves any chosen particular vector in its 8-dimensional real
that preserves any chosen particular vector in its 8-dimensional real
spinor
representation
.
In older books and papers, G2 is sometimes denoted by E2.
a 2-dimensional space, as drawn, it's much more symmetric to consider them as vectors
in a 2-dimensional subspace of a three dimensional space.
Simple roots, (1,−2,1)
/Coxeter
group is the dihedral group
, D6 of order 12.
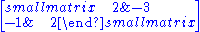
group of a Riemannian metric. The manifold
s of G2 holonomy are also called G2-manifolds
.
 is the automorphism group of the following two polynomials in 7 non-commutative variables.
is the automorphism group of the following two polynomials in 7 non-commutative variables.

 (± permutations)
(± permutations)
which comes from the octionion algebra. The variables must be non-commutative otherwise the second polynomial would be identically zero.
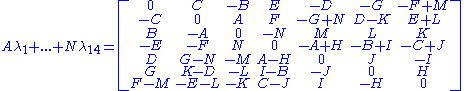
. The dimensions of the smallest irreducible representations are :
The 14-dimensional representation is the adjoint representation, and the 7-dimensional one is action of G2 on the imaginary octonions.
There are two non-isomorphic irreducible representations of dimensions 77, 2079, 4928, 28652, etc. The fundamental representation
s are those with dimensions 14 and 7 (corresponding to the two nodes in the Dynkin diagram in the order such that the triple arrow points from the first to the second).
described the (infinite dimensional) unitary irreducible representations of the.split real form of G2.
introduced the finite groups G2(Fq) in for odd q and for even q. The group G2(Fq) is the points of the algebraic group G2 over the finite field
Fq. The order of the group is . When q ≠ 2, the group is simple
, and when q = 2, it has a simple subgroup of index
2 isomorphic to 2A2(32). The Janko group J1
was first constructed as a subgroup of G2(F11). introduced twisted Ree groups 2G2(Fq) of order q3(q3+1)(q−1) for q=32n+1 an odd power of 3.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, G2 is the name of three simple Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s (a complex form, a compact real form and a split real form), their Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s
 , as well as some algebraic group
, as well as some algebraic groupAlgebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s. They are the smallest of the five exceptional simple Lie group
Simple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
s. G2 has rank 2 and dimension 14. Its fundamental representation
Fundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
is 7-dimensional.
The compact form of G2 can be described as the automorphism group of the octonion algebra
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
or, equivalently, as the subgroup of
 that preserves any chosen particular vector in its 8-dimensional real
that preserves any chosen particular vector in its 8-dimensional realReal representation
In the mathematical field of representation theory a real representation is usually a representation on a real vector space U, but it can also mean a representation on a complex vector space V with an invariant real structure, i.e., an antilinear equivariant mapj\colon V\to V\,which...
spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
.
In older books and papers, G2 is sometimes denoted by E2.
Real forms
There are 3 simple real Lie algebras associated with this root system:- The underlying real Lie algebra of the complex Lie algebra G2 has dimension 28. It has complex conjugation as an outer automorphism and is simply connected. The maximal compact subgroup of its associated group is the compact form of G2.
- The Lie algebra of the compact form is 14 dimensional. The associated Lie group has no outer automorphisms, no center, and is simply connected and compact.
- The Lie algebra of the non-compact (split) form has dimension 14. The associated simple Lie group has fundamental group of order 2 and its outer automorphism groupOuter automorphism groupIn mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
is the trivial group. Its maximal compact subgroup is SU(2)×SU(2)/(−1×−1). It has a non-algebraic double cover that is simply connected.
Algebra
Roots of G2
Although they spanLinear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
a 2-dimensional space, as drawn, it's much more symmetric to consider them as vectors
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
in a 2-dimensional subspace of a three dimensional space.
| , (−1,1,0), (−1,0,1), (0,−1,1) | , (−2,1,1), (−1,2,−1), (−1,−1,2) |
Simple roots, (1,−2,1)
Weyl/Coxeter group
Its WeylWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
/Coxeter
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
group is the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
, D6 of order 12.
Cartan matrix
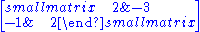
Special holonomy
G2 is one of the possible special groups that can appear as the holonomyHolonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
group of a Riemannian metric. The manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s of G2 holonomy are also called G2-manifolds
G2 manifold
In differential geometry, a G2 manifold is a seven-dimensional Riemannian manifold with holonomy group G2. The group G_2 is one of the five exceptional simple Lie groups...
.
Polynomial Invariant
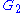 is the automorphism group of the following two polynomials in 7 non-commutative variables.
is the automorphism group of the following two polynomials in 7 non-commutative variables.
 (± permutations)
(± permutations)which comes from the octionion algebra. The variables must be non-commutative otherwise the second polynomial would be identically zero.
Generators
Adding a representation of the 14 generators with coefficients A..N gives the matrix: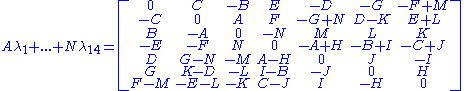
Representations
The characters of finite dimensional representations of the real and complex Lie algebras and Lie groups are all given by the Weyl character formulaWeyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
. The dimensions of the smallest irreducible representations are :
- 1, 7, 14, 27, 64, 77 (twice), 182, 189, 273, 286, 378, 448, 714, 729, 748, 896, 924, 1254, 1547, 1728, 1729, 2079 (twice), 2261, 2926, 3003, 3289, 3542, 4096, 4914, 4928 (twice), 5005, 5103, 6630, 7293, 7371, 7722, 8372, 9177, 9660, 10206, 10556, 11571, 11648, 12096, 13090….
The 14-dimensional representation is the adjoint representation, and the 7-dimensional one is action of G2 on the imaginary octonions.
There are two non-isomorphic irreducible representations of dimensions 77, 2079, 4928, 28652, etc. The fundamental representation
Fundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
s are those with dimensions 14 and 7 (corresponding to the two nodes in the Dynkin diagram in the order such that the triple arrow points from the first to the second).
described the (infinite dimensional) unitary irreducible representations of the.split real form of G2.
Finite groups
Leonard Eugene DicksonLeonard Eugene Dickson
Leonard Eugene Dickson was an American mathematician. He was one of the first American researchers in abstract algebra, in particular the theory of finite fields and classical groups, and is also remembered for a three-volume history of number theory.-Life:Dickson considered himself a Texan by...
introduced the finite groups G2(Fq) in for odd q and for even q. The group G2(Fq) is the points of the algebraic group G2 over the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
Fq. The order of the group is . When q ≠ 2, the group is simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
, and when q = 2, it has a simple subgroup of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2 isomorphic to 2A2(32). The Janko group J1
Janko group J1
In mathematics, the smallest Janko group, J1, is a simple sporadic group of order 175560. It was originally described by Zvonimir Janko and was the first sporadic group to be found since the discovery of the Mathieu groups in the 19th century...
was first constructed as a subgroup of G2(F11). introduced twisted Ree groups 2G2(Fq) of order q3(q3+1)(q−1) for q=32n+1 an odd power of 3.

