Fuzzy control system
Encyclopedia
A fuzzy control system is a control system based on fuzzy logic
—a mathematical
system that analyzes analog
input values in terms of logic
al variables that take on continuous values between 0 and 1, in contrast to classical or digital
logic, which operates on discrete values of either 1 or 0 (true or false respectively).
built in Denmark, coming on line in 1975.
Fuzzy systems were largely ignored in the U.S. because they were associated with artificial intelligence
, a field that periodically oversells itself, especially in the mid-1980s, resulting in a lack of credibility within the commercial domain.
The Japanese did not have this prejudice. Interest in fuzzy systems was sparked by Seiji Yasunobu and Soji Miyamoto of Hitachi
, who in 1985 provided simulations that demonstrated the superiority of fuzzy control systems for the Sendai railway. Their ideas were adopted, and fuzzy systems were used to control accelerating, braking, and stopping when the line opened in 1987.
Another event in 1987 helped promote interest in fuzzy systems. During an international meeting of fuzzy researchers in Tokyo that year, Takeshi Yamakawa demonstrated the use of fuzzy control, through a set of simple dedicated fuzzy logic chips, in an "inverted pendulum
" experiment. This is a classic control problem, in which a vehicle tries to keep a pole mounted on its top by a hinge upright by moving back and forth.
Observers were impressed with this demonstration, as well as later experiments by Yamakawa in which he mounted a wine glass containing water or even a live mouse to the top of the pendulum. The system maintained stability in both cases. Yamakawa eventually went on to organize his own fuzzy-systems research lab to help exploit his patents in the field.
Following such demonstrations, Japanese engineers developed a wide range of fuzzy systems for both industrial and consumer applications. In 1988 Japan established the Laboratory for International Fuzzy Engineering (LIFE), a cooperative arrangement between 48 companies to pursue fuzzy research.
Japanese consumer goods often incorporate fuzzy systems. Matsushita vacuum cleaners use microcontrollers running fuzzy algorithms to interrogate dust sensors and adjust suction power accordingly. Hitachi washing machines use fuzzy controllers to load-weight, fabric-mix, and dirt sensors and automatically set the wash cycle for the best use of power, water, and detergent.
As a more specific example, Canon developed an autofocus
ing camera that uses a charge-coupled device
(CCD) to measure the clarity of the image in six regions of its field of view and use the information provided to determine if the image is in focus. It also tracks the rate of change of lens movement during focusing, and controls its speed to prevent overshoot.
The camera's fuzzy control system uses 12 inputs: 6 to obtain the current clarity data provided by the CCD and 6 to measure the rate of change of lens movement. The output is the position of the lens. The fuzzy control system uses 13 rules and requires 1.1 kilobytes of memory.
As another example of a practical system, an industrial air conditioner designed by Mitsubishi uses 25 heating rules and 25 cooling rules. A temperature sensor provides input, with control outputs fed to an inverter
, a compressor valve, and a fan motor. Compared to the previous design, the fuzzy controller heats and cools five times faster, reduces power consumption by 24%, increases temperature stability by a factor of two, and uses fewer sensors.
The enthusiasm of the Japanese for fuzzy logic is reflected in the wide range of other applications they have investigated or implemented: character and handwriting recognition; optical fuzzy systems; robots, including one for making Japanese flower arrangements; voice-controlled robot helicopters, this being no mean feat, as hovering is a "balancing act" rather similar to the inverted pendulum problem; control of flow of powders in film manufacture; elevator systems; and so on.
Work on fuzzy systems is also proceeding in the US and Europe, though not with the same enthusiasm shown in Japan. The US Environmental Protection Agency has investigated fuzzy control for energy-efficient
motors, and NASA
has studied fuzzy control for automated space docking: simulations show that a fuzzy control system can greatly reduce fuel consumption. Firms such as Boeing, General Motors, Allen-Bradley, Chrysler, Eaton, and Whirlpool have worked on fuzzy logic for use in low-power refrigerators, improved automotive transmissions, and energy-efficient electric motors.
In 1995 Maytag introduced an "intelligent" dishwasher
based on a fuzzy controller and a "one-stop sensing module" that combines a thermistor
, for temperature measurement; a conductivity sensor, to measure detergent level from the ions present in the wash; a turbidity sensor that measures scattered and transmitted light to measure the soiling of the wash; and a magnetostrictive sensor to read spin rate. The system determines the optimum wash cycle for any load to obtain the best results with the least amount of energy, detergent, and water. It even adjusts for dried-on foods by tracking the last time the door was opened, and estimates the number of dishes by the number of times the door was opened.
Research and development is also continuing on fuzzy applications in software, as opposed to firmware
, design, including fuzzy expert system
s and integration of fuzzy logic with neural-network
and so-called adaptive "genetic
" software systems, with the ultimate goal of building "self-learning" fuzzy control systems.
A control system may also have various types of switch
, or "ON-OFF", inputs along with its analog inputs, and such switch inputs of course will always have a truth value equal to either 1 or 0, but the scheme can deal with them as simplified fuzzy functions that happen to be either one value or another.
Given "mapping
s" of input variables into membership functions and truth values, the microcontroller
then makes decisions
for what action to take based on a set of "rules", each of the form:
IF brake temperature IS warm AND speed IS not very fast
THEN brake pressure IS slightly decreased.
In this example, the two input variables are "brake temperature" and "speed" that have values defined as fuzzy sets. The output variable, "brake pressure", is also defined by a fuzzy set that can have values like "static", "slightly increased", "slightly decreased", and so on.
This rule by itself is very puzzling since it looks like it could be used without bothering with fuzzy logic, but remember that the decision is based on a set of rules:
This combination of fuzzy operations and rule-based
"inference
" describes a "fuzzy expert system".
Traditional control systems are based on mathematical models in which the control system is described using one or more differential equation
s that define the system response to its inputs. Such systems are often implemented as "PID controllers" (proportional-integral-derivative controllers
). They are the products of decades of development and theoretical analysis, and are highly effective.
If PID and other traditional control systems are so well-developed, why bother with fuzzy control? It has some advantages. In many cases, the mathematical model of the control process may not exist, or may be too "expensive" in terms of computer processing power and memory, and a system based on empirical rules may be more effective.
Furthermore, fuzzy logic is well suited to low-cost implementations based on cheap sensors, low-resolution analog-to-digital converters, and 4-bit or 8-bit one-chip microcontroller chips. Such systems can be easily upgraded by adding new rules to improve performance or add new features. In many cases, fuzzy control can be used to improve existing traditional controller systems by adding an extra layer of intelligence to the current control method.
The most common shape of membership functions is triangular, although trapezoidal and bell curves are also used, but the shape is generally less important than the number of curves and their placement. From three to seven curves are generally appropriate to cover the required range of an input value, or the "universe of discourse" in fuzzy jargon.
As discussed earlier, the processing stage is based on a collection of logic rules in the form of IF-THEN statements, where the IF part is called the "antecedent" and the THEN part is called the "consequent". Typical fuzzy control systems have dozens of rules.
Consider a rule for a thermostat:
IF (temperature is "cold") THEN (heater is "high")
This rule uses the truth value of the "temperature" input, which is some truth value of "cold", to generate a result in the fuzzy set for the "heater" output, which is some value of "high". This result is used with the results of other rules to finally generate the crisp composite output. Obviously, the greater the truth value of "cold", the higher the truth value of "high", though this does not necessarily mean that the output itself will be set to "high", since this is only one rule among many.
In some cases, the membership functions can be modified by "hedges" that are equivalent to adjectives. Common hedges include "about", "near", "close to", "approximately", "very", "slightly", "too", "extremely", and "somewhat". These operations may have precise definitions, though the definitions can vary considerably between different implementations. "Very", for one example, squares membership functions; since the membership values are always less than 1, this narrows the membership function. "Extremely" cubes the values to give greater narrowing, while "somewhat" broadens the function by taking the square root.
In practice, the fuzzy rule sets usually have several antecedents that are combined using fuzzy operators, such as AND, OR, and NOT, though again the definitions tend to vary: AND, in one popular definition, simply uses the minimum weight of all the antecedents, while OR uses the maximum value. There is also a NOT operator that subtracts a membership function from 1 to give the "complementary" function.
There are several different ways to define the result of a rule, but one of the most common and simplest is the "max-min" inference method, in which the output membership function is given the truth value generated by the premise.
Rules can be solved in parallel in hardware, or sequentially in software. The results of all the rules that have fired are "defuzzified" to a crisp value by one of several methods. There are dozens in theory, each with various advantages and drawbacks.
The "centroid" method is very popular, in which the "center of mass" of the result provides the crisp value. Another approach is the "height" method, which takes the value of the biggest contributor. The centroid method favors the rule with the output of greatest area, while the height method obviously favors the rule with the greatest output value.
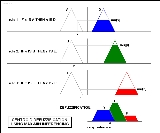
The diagram below demonstrates max-min inferencing and centroid defuzzification for a system with input variables "x", "y", and "z" and an output variable "n". Note that "mu" is standard fuzzy-logic nomenclature for "truth value":
Notice how each rule provides a result as a truth value of a particular membership function for the output variable. In centroid defuzzification the values are OR'd, that is, the maximum value is used and values are not added, and the results are then combined using a centroid calculation.
Fuzzy control system design is based on empirical methods, basically a methodical approach to trial-and-error. The general process is as follows:
As a general example, consider the design of a fuzzy controller for a steam turbine. The block diagram of this control system appears as follows:
The input and output variables map into the following fuzzy set:
-- where:
N3: Large negative.
N2: Medium negative.
N1: Small negative.
Z: Zero.
P1: Small positive.
P2: Medium positive.
P3: Large positive.
The rule set includes such rules as:
rule 1: IF temperature IS cool AND pressure IS weak,
THEN throttle is P3.
rule 2: IF temperature IS cool AND pressure IS low,
THEN throttle is P2.
rule 3: IF temperature IS cool AND pressure IS ok,
THEN throttle is Z.
rule 4: IF temperature IS cool AND pressure IS strong,
THEN throttle is N2.
In practice, the controller accepts the inputs and maps them into their membership functions and truth values. These mappings are then fed into the rules. If the rule specifies an AND relationship between the mappings of the two input variables, as the examples above do, the minimum of the two is used as the combined truth value; if an OR is specified, the maximum is used. The appropriate output state is selected and assigned a membership value at the truth level of the premise. The truth values are then defuzzified.
For an example, assume the temperature is in the "cool" state, and the pressure is in the "low" and "ok" states. The pressure values ensure that only rules 2 and 3 fire:
The two outputs are then defuzzified through centroid defuzzification:
The output value will adjust the throttle and then the control cycle will begin again to generate the next value.
A fuzzy set is defined for the input error variable "e", and the derived change in error, "delta", as well as the "output", as follows:
LP: large positive
SP: small positive
ZE: zero
SN: small negative
LN: large negative
If the error ranges from -1 to +1, with the analog-to-digital converter used having a resolution of 0.25, then the input variable's fuzzy set (which, in this case, also applies to the output variable) can be described very simply as a table, with the error / delta / output values in the top row and the truth values for each membership function arranged in rows beneath:
_______________________________________________________________________
-1 -0.75 -0.5 -0.25 0 0.25 0.5 0.75 1
_______________________________________________________________________
mu(LP) 0 0 0 0 0 0 0.3 0.7 1
mu(SP) 0 0 0 0 0.3 0.7 1 0.7 0.3
mu(ZE) 0 0 0.3 0.7 1 0.7 0.3 0 0
mu(SN) 0.3 0.7 1 0.7 0.3 0 0 0 0
mu(LN) 1 0.7 0.3 0 0 0 0 0 0
_______________________________________________________________________—or, in graphical form (where each "X" has a value of 0.1):
LN SN ZE SP LP
+------------------------------------------------------------------+
| |
-1.0 | XXXXXXXXXX XXX : : : |
-0.75 | XXXXXXX XXXXXXX : : : |
-0.5 | XXX XXXXXXXXXX XXX : : |
-0.25 | : XXXXXXX XXXXXXX : : |
0.0 | : XXX XXXXXXXXXX XXX : |
0.25 | : : XXXXXXX XXXXXXX : |
0.5 | : : XXX XXXXXXXXXX XXX |
0.75 | : : : XXXXXXX XXXXXXX |
1.0 | : : : XXX XXXXXXXXXX |
| |
+------------------------------------------------------------------+
Suppose this fuzzy system has the following rule base:
rule 1: IF e = ZE AND delta = ZE THEN output = ZE
rule 2: IF e = ZE AND delta = SP THEN output = SN
rule 3: IF e = SN AND delta = SN THEN output = LP
rule 4: IF e = LP OR delta = LP THEN output = LN
These rules are typical for control applications in that the antecedents consist of the logical combination of the error and error-delta signals, while the consequent is a control command output.
The rule outputs can be defuzzified using a discrete centroid computation:
SUM( I = 1 TO 4 OF ( mu(I) * output(I) ) ) / SUM( I = 1 TO 4 OF mu(I) )
Now, suppose that at a given time we have:
e = 0.25
delta = 0.5
Then this gives:
________________________
e delta
________________________
mu(LP) 0 0.3
mu(SP) 0.7 1
mu(ZE) 0.7 0.3
mu(SN) 0 0
mu(LN) 0 0
________________________
Plugging this into rule 1 gives:
rule 1: IF e = ZE AND delta = ZE THEN output = ZE
mu(1) = MIN( 0.7, 0.3 ) = 0.3
output(1) = 0
-- where:
The other rules give:
rule 2: IF e = ZE AND delta = SP THEN output = SN
mu(2) = MIN( 0.7, 1 ) = 0.7
output(2) = -0.5
rule 3: IF e = SN AND delta = SN THEN output = LP
mu(3) = MIN( 0.0, 0.0 ) = 0
output(3) = 1
rule 4: IF e = LP OR delta = LP THEN output = LN
mu(4) = MAX( 0.0, 0.3 ) = 0.3
output(4) = -1
The centroid computation yields:
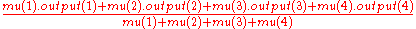
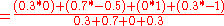
-- for the final control output. Simple. Of course the hard part is figuring out what rules actually work correctly in practice.
If you have problems figuring out the centroid equation, remember that a centroid is defined by summing all the moments (location times mass) around the center of gravity and equating the sum to zero. So if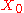
is the center of gravity, 
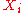is the location of each mass, and 
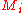is each mass, this gives:
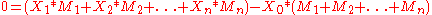
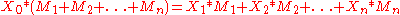
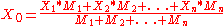
In our example, the values of mu correspond to the masses, and the values of X to location of the masses
(mu, however, only 'corresponds to the masses' if the initial 'mass' of the output functions are all the same/equivalent. If they are not the same, i.e. some are narrow triangles, while others maybe wide trapizoids or shouldered triangles, then the mass or area of the output function must be known or calculated. It is this mass that is then scaled by mu and multiplied by its location X_i).
This system can be implemented on a standard microprocessor, but dedicated fuzzy chips are now available. For example, Adaptive Logic INC of San Jose, California, sells a "fuzzy chip", the AL220, that can accept four analog inputs and generate four analog outputs. A block diagram of the chip is shown below:
, directed by a microcontroller chip. The microcontroller has to make decisions based on brake temperature
, speed
, and other variables in the system.
The variable "temperature" in this system can be subdivided into a range of "states": "cold", "cool", "moderate", "warm", "hot", "very hot". The transition from one state to the next is hard to define.
An arbitrary static threshold might be set to divide "warm" from "hot". For example, at exactly 90 degrees, warm ends and hot begins. But this would result in a discontinuous change when the input value passed over that threshold. The transition wouldn't be smooth, as would be required in braking situations.
The way around this is to make the states fuzzy. That is, allow them to change gradually from one state to the next. In order to do this there must be a dynamic relationship established between different factors.
We start by defining the input temperature states using "membership functions":
With this scheme, the input variable's state no longer jumps abruptly from one state to the next. Instead, as the temperature changes, it loses value in one membership function while gaining value in the next. In other words, its ranking in the category of cold decreases as it becomes more highly ranked in the warmer category.
At any sampled timeframe, the "truth value" of the brake temperature will almost always be in some degree part of two membership functions: i.e.: '0.6 nominal and 0.4 warm', or '0.7 nominal and 0.3 cool', and so on.
The above example demonstrates a simple application, using the abstraction
of values from multiple values. This only represents one kind of data, however, in this case, temperature.
Adding additional sophistication to this braking system, could be done by additional factors such as traction
, speed, inertia
, set up in dynamic functions, according to the designed fuzzy system.
Fuzzy logic
Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
—a mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
system that analyzes analog
Analog signal
An analog or analogue signal is any continuous signal for which the time varying feature of the signal is a representation of some other time varying quantity, i.e., analogous to another time varying signal. It differs from a digital signal in terms of small fluctuations in the signal which are...
input values in terms of logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
al variables that take on continuous values between 0 and 1, in contrast to classical or digital
Digital
A digital system is a data technology that uses discrete values. By contrast, non-digital systems use a continuous range of values to represent information...
logic, which operates on discrete values of either 1 or 0 (true or false respectively).
Overview
Fuzzy logic is widely used in machine control. The term itself inspires a certain skepticism, sounding equivalent to "half-baked logic" or "bogus logic", but the "fuzzy" part does not refer to a lack of rigour in the method, rather to the fact that the logic involved can deal with fuzzy concepts—concepts that cannot be expressed as "true" or "false" but rather as "partially true". Although genetic algorithms and neural networks can perform just as well as fuzzy logic in many cases, fuzzy logic has the advantage that the solution to the problem can be cast in terms that human operators can understand, so that their experience can be used in the design of the controller. This makes it easier to mechanize tasks that are already successfully performed by humans.History and applications
Fuzzy logic was first proposed by Lotfi A. Zadeh of the University of California at Berkeley in a 1965 paper. He elaborated on his ideas in a 1973 paper that introduced the concept of "linguistic variables", which in this article equates to a variable defined as a fuzzy set. Other research followed, with the first industrial application, a cement kilnKiln
A kiln is a thermally insulated chamber, or oven, in which a controlled temperature regime is produced. Uses include the hardening, burning or drying of materials...
built in Denmark, coming on line in 1975.
Fuzzy systems were largely ignored in the U.S. because they were associated with artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
, a field that periodically oversells itself, especially in the mid-1980s, resulting in a lack of credibility within the commercial domain.
The Japanese did not have this prejudice. Interest in fuzzy systems was sparked by Seiji Yasunobu and Soji Miyamoto of Hitachi
Hitachi
Hitachi is a multinational corporation specializing in high-technology.Hitachi may also refer to:*Hitachi, Ibaraki, Japan*Hitachi province, former province of Japan*Prince Hitachi and Princess Hitachi, members of the Japanese imperial family...
, who in 1985 provided simulations that demonstrated the superiority of fuzzy control systems for the Sendai railway. Their ideas were adopted, and fuzzy systems were used to control accelerating, braking, and stopping when the line opened in 1987.
Another event in 1987 helped promote interest in fuzzy systems. During an international meeting of fuzzy researchers in Tokyo that year, Takeshi Yamakawa demonstrated the use of fuzzy control, through a set of simple dedicated fuzzy logic chips, in an "inverted pendulum
Inverted pendulum
An inverted pendulum is a pendulum which has its mass above its pivot point. It is often implemented with the pivot point mounted on a cart that can move horizontally and may be called a cart and pole...
" experiment. This is a classic control problem, in which a vehicle tries to keep a pole mounted on its top by a hinge upright by moving back and forth.
Observers were impressed with this demonstration, as well as later experiments by Yamakawa in which he mounted a wine glass containing water or even a live mouse to the top of the pendulum. The system maintained stability in both cases. Yamakawa eventually went on to organize his own fuzzy-systems research lab to help exploit his patents in the field.
Following such demonstrations, Japanese engineers developed a wide range of fuzzy systems for both industrial and consumer applications. In 1988 Japan established the Laboratory for International Fuzzy Engineering (LIFE), a cooperative arrangement between 48 companies to pursue fuzzy research.
Japanese consumer goods often incorporate fuzzy systems. Matsushita vacuum cleaners use microcontrollers running fuzzy algorithms to interrogate dust sensors and adjust suction power accordingly. Hitachi washing machines use fuzzy controllers to load-weight, fabric-mix, and dirt sensors and automatically set the wash cycle for the best use of power, water, and detergent.
As a more specific example, Canon developed an autofocus
Autofocus
An autofocus optical system uses a sensor, a control system and a motor to focus fully automatic or on a manually selected point or area. An electronic rangefinder has a display instead of the motor; the adjustment of the optical system has to be done manually until indication...
ing camera that uses a charge-coupled device
Charge-coupled device
A charge-coupled device is a device for the movement of electrical charge, usually from within the device to an area where the charge can be manipulated, for example conversion into a digital value. This is achieved by "shifting" the signals between stages within the device one at a time...
(CCD) to measure the clarity of the image in six regions of its field of view and use the information provided to determine if the image is in focus. It also tracks the rate of change of lens movement during focusing, and controls its speed to prevent overshoot.
The camera's fuzzy control system uses 12 inputs: 6 to obtain the current clarity data provided by the CCD and 6 to measure the rate of change of lens movement. The output is the position of the lens. The fuzzy control system uses 13 rules and requires 1.1 kilobytes of memory.
As another example of a practical system, an industrial air conditioner designed by Mitsubishi uses 25 heating rules and 25 cooling rules. A temperature sensor provides input, with control outputs fed to an inverter
Inverter (logic gate)
In digital logic, an inverter or NOT gate is a logic gate which implements logical negation. The truth table is shown on the right.This represents perfect switching behavior, which is the defining assumption in Digital electronics. In practice, actual devices have electrical characteristics that...
, a compressor valve, and a fan motor. Compared to the previous design, the fuzzy controller heats and cools five times faster, reduces power consumption by 24%, increases temperature stability by a factor of two, and uses fewer sensors.
The enthusiasm of the Japanese for fuzzy logic is reflected in the wide range of other applications they have investigated or implemented: character and handwriting recognition; optical fuzzy systems; robots, including one for making Japanese flower arrangements; voice-controlled robot helicopters, this being no mean feat, as hovering is a "balancing act" rather similar to the inverted pendulum problem; control of flow of powders in film manufacture; elevator systems; and so on.
Work on fuzzy systems is also proceeding in the US and Europe, though not with the same enthusiasm shown in Japan. The US Environmental Protection Agency has investigated fuzzy control for energy-efficient
Efficient energy use
Efficient energy use, sometimes simply called energy efficiency, is the goal of efforts to reduce the amount of energy required to provide products and services. For example, insulating a home allows a building to use less heating and cooling energy to achieve and maintain a comfortable temperature...
motors, and NASA
NASA
The National Aeronautics and Space Administration is the agency of the United States government that is responsible for the nation's civilian space program and for aeronautics and aerospace research...
has studied fuzzy control for automated space docking: simulations show that a fuzzy control system can greatly reduce fuel consumption. Firms such as Boeing, General Motors, Allen-Bradley, Chrysler, Eaton, and Whirlpool have worked on fuzzy logic for use in low-power refrigerators, improved automotive transmissions, and energy-efficient electric motors.
In 1995 Maytag introduced an "intelligent" dishwasher
Dishwasher
A dishwasher is a mechanical device for cleaning dishes and eating utensils. Dishwashers can be found in restaurants and private homes.Unlike manual dishwashing, which relies largely on physical scrubbing to remove soiling, the mechanical dishwasher cleans by spraying hot water, typically between ...
based on a fuzzy controller and a "one-stop sensing module" that combines a thermistor
Thermistor
A thermistor is a type of resistor whose resistance varies significantly with temperature, more so than in standard resistors. The word is a portmanteau of thermal and resistor...
, for temperature measurement; a conductivity sensor, to measure detergent level from the ions present in the wash; a turbidity sensor that measures scattered and transmitted light to measure the soiling of the wash; and a magnetostrictive sensor to read spin rate. The system determines the optimum wash cycle for any load to obtain the best results with the least amount of energy, detergent, and water. It even adjusts for dried-on foods by tracking the last time the door was opened, and estimates the number of dishes by the number of times the door was opened.
Research and development is also continuing on fuzzy applications in software, as opposed to firmware
Firmware
In electronic systems and computing, firmware is a term often used to denote the fixed, usually rather small, programs and/or data structures that internally control various electronic devices...
, design, including fuzzy expert system
Expert system
In artificial intelligence, an expert system is a computer system that emulates the decision-making ability of a human expert. Expert systems are designed to solve complex problems by reasoning about knowledge, like an expert, and not by following the procedure of a developer as is the case in...
s and integration of fuzzy logic with neural-network
Neural network
The term neural network was traditionally used to refer to a network or circuit of biological neurons. The modern usage of the term often refers to artificial neural networks, which are composed of artificial neurons or nodes...
and so-called adaptive "genetic
Genetic algorithm
A genetic algorithm is a search heuristic that mimics the process of natural evolution. This heuristic is routinely used to generate useful solutions to optimization and search problems...
" software systems, with the ultimate goal of building "self-learning" fuzzy control systems.
Fuzzy sets
The input variables in a fuzzy control system are in general mapped into by sets of membership functions similar to this, known as "fuzzy sets". The process of converting a crisp input value to a fuzzy value is called "fuzzification".A control system may also have various types of switch
Switch
In electronics, a switch is an electrical component that can break an electrical circuit, interrupting the current or diverting it from one conductor to another....
, or "ON-OFF", inputs along with its analog inputs, and such switch inputs of course will always have a truth value equal to either 1 or 0, but the scheme can deal with them as simplified fuzzy functions that happen to be either one value or another.
Given "mapping
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
s" of input variables into membership functions and truth values, the microcontroller
Microcontroller
A microcontroller is a small computer on a single integrated circuit containing a processor core, memory, and programmable input/output peripherals. Program memory in the form of NOR flash or OTP ROM is also often included on chip, as well as a typically small amount of RAM...
then makes decisions
Decision making
Decision making can be regarded as the mental processes resulting in the selection of a course of action among several alternative scenarios. Every decision making process produces a final choice. The output can be an action or an opinion of choice.- Overview :Human performance in decision terms...
for what action to take based on a set of "rules", each of the form:
IF brake temperature IS warm AND speed IS not very fast
THEN brake pressure IS slightly decreased.
In this example, the two input variables are "brake temperature" and "speed" that have values defined as fuzzy sets. The output variable, "brake pressure", is also defined by a fuzzy set that can have values like "static", "slightly increased", "slightly decreased", and so on.
This rule by itself is very puzzling since it looks like it could be used without bothering with fuzzy logic, but remember that the decision is based on a set of rules:
- All the rules that apply are invoked, using the membership functions and truth values obtained from the inputs, to determine the result of the rule.
- This result in turn will be mapped into a membership function and truth value controlling the output variable.
- These results are combined to give a specific ("crisp") answer, the actual brake pressure, a procedure known as "defuzzificationDefuzzificationDefuzzification is the process of producing a quantifiable result in fuzzy logic, given fuzzy sets and corresponding membership degrees. It is typically needed in fuzzy control systems. These will have a number of rules that transform a number of variables into a fuzzy result, that is, the result...
".
This combination of fuzzy operations and rule-based
Rule-based system
In computer science, rule-based systems are used as a way to store and manipulate knowledge to interpret information in a useful way. They are often used in artificial intelligence applications and research.-Applications:...
"inference
Inference
Inference is the act or process of deriving logical conclusions from premises known or assumed to be true. The conclusion drawn is also called an idiomatic. The laws of valid inference are studied in the field of logic.Human inference Inference is the act or process of deriving logical conclusions...
" describes a "fuzzy expert system".
Traditional control systems are based on mathematical models in which the control system is described using one or more differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s that define the system response to its inputs. Such systems are often implemented as "PID controllers" (proportional-integral-derivative controllers
PID controller
A proportional–integral–derivative controller is a generic control loop feedback mechanism widely used in industrial control systems – a PID is the most commonly used feedback controller. A PID controller calculates an "error" value as the difference between a measured process variable and a...
). They are the products of decades of development and theoretical analysis, and are highly effective.
If PID and other traditional control systems are so well-developed, why bother with fuzzy control? It has some advantages. In many cases, the mathematical model of the control process may not exist, or may be too "expensive" in terms of computer processing power and memory, and a system based on empirical rules may be more effective.
Furthermore, fuzzy logic is well suited to low-cost implementations based on cheap sensors, low-resolution analog-to-digital converters, and 4-bit or 8-bit one-chip microcontroller chips. Such systems can be easily upgraded by adding new rules to improve performance or add new features. In many cases, fuzzy control can be used to improve existing traditional controller systems by adding an extra layer of intelligence to the current control method.
Fuzzy control in detail
Fuzzy controllers are very simple conceptually. They consist of an input stage, a processing stage, and an output stage. The input stage maps sensor or other inputs, such as switches, thumbwheels, and so on, to the appropriate membership functions and truth values. The processing stage invokes each appropriate rule and generates a result for each, then combines the results of the rules. Finally, the output stage converts the combined result back into a specific control output value.The most common shape of membership functions is triangular, although trapezoidal and bell curves are also used, but the shape is generally less important than the number of curves and their placement. From three to seven curves are generally appropriate to cover the required range of an input value, or the "universe of discourse" in fuzzy jargon.
As discussed earlier, the processing stage is based on a collection of logic rules in the form of IF-THEN statements, where the IF part is called the "antecedent" and the THEN part is called the "consequent". Typical fuzzy control systems have dozens of rules.
Consider a rule for a thermostat:
IF (temperature is "cold") THEN (heater is "high")
This rule uses the truth value of the "temperature" input, which is some truth value of "cold", to generate a result in the fuzzy set for the "heater" output, which is some value of "high". This result is used with the results of other rules to finally generate the crisp composite output. Obviously, the greater the truth value of "cold", the higher the truth value of "high", though this does not necessarily mean that the output itself will be set to "high", since this is only one rule among many.
In some cases, the membership functions can be modified by "hedges" that are equivalent to adjectives. Common hedges include "about", "near", "close to", "approximately", "very", "slightly", "too", "extremely", and "somewhat". These operations may have precise definitions, though the definitions can vary considerably between different implementations. "Very", for one example, squares membership functions; since the membership values are always less than 1, this narrows the membership function. "Extremely" cubes the values to give greater narrowing, while "somewhat" broadens the function by taking the square root.
In practice, the fuzzy rule sets usually have several antecedents that are combined using fuzzy operators, such as AND, OR, and NOT, though again the definitions tend to vary: AND, in one popular definition, simply uses the minimum weight of all the antecedents, while OR uses the maximum value. There is also a NOT operator that subtracts a membership function from 1 to give the "complementary" function.
There are several different ways to define the result of a rule, but one of the most common and simplest is the "max-min" inference method, in which the output membership function is given the truth value generated by the premise.
Rules can be solved in parallel in hardware, or sequentially in software. The results of all the rules that have fired are "defuzzified" to a crisp value by one of several methods. There are dozens in theory, each with various advantages and drawbacks.
The "centroid" method is very popular, in which the "center of mass" of the result provides the crisp value. Another approach is the "height" method, which takes the value of the biggest contributor. The centroid method favors the rule with the output of greatest area, while the height method obviously favors the rule with the greatest output value.
The diagram below demonstrates max-min inferencing and centroid defuzzification for a system with input variables "x", "y", and "z" and an output variable "n". Note that "mu" is standard fuzzy-logic nomenclature for "truth value":
Notice how each rule provides a result as a truth value of a particular membership function for the output variable. In centroid defuzzification the values are OR'd, that is, the maximum value is used and values are not added, and the results are then combined using a centroid calculation.
Fuzzy control system design is based on empirical methods, basically a methodical approach to trial-and-error. The general process is as follows:
- Document the system's operational specifications and inputs and outputs.
- Document the fuzzy sets for the inputs.
- Document the rule set.
- Determine the defuzzification method.
- Run through test suite to validate system, adjust details as required.
- Complete document and release to production.
As a general example, consider the design of a fuzzy controller for a steam turbine. The block diagram of this control system appears as follows:
The input and output variables map into the following fuzzy set:
-- where:
N3: Large negative.
N2: Medium negative.
N1: Small negative.
Z: Zero.
P1: Small positive.
P2: Medium positive.
P3: Large positive.
The rule set includes such rules as:
rule 1: IF temperature IS cool AND pressure IS weak,
THEN throttle is P3.
rule 2: IF temperature IS cool AND pressure IS low,
THEN throttle is P2.
rule 3: IF temperature IS cool AND pressure IS ok,
THEN throttle is Z.
rule 4: IF temperature IS cool AND pressure IS strong,
THEN throttle is N2.
In practice, the controller accepts the inputs and maps them into their membership functions and truth values. These mappings are then fed into the rules. If the rule specifies an AND relationship between the mappings of the two input variables, as the examples above do, the minimum of the two is used as the combined truth value; if an OR is specified, the maximum is used. The appropriate output state is selected and assigned a membership value at the truth level of the premise. The truth values are then defuzzified.
For an example, assume the temperature is in the "cool" state, and the pressure is in the "low" and "ok" states. The pressure values ensure that only rules 2 and 3 fire:
The two outputs are then defuzzified through centroid defuzzification:
__________________________________________________________________
| Z P2
1 -+ * *
| * * * *
| * * * *
| * * * *
| * 222222222
| * 22222222222
| 333333332222222222222
+---33333333222222222222222-->
^
+150
__________________________________________________________________
The output value will adjust the throttle and then the control cycle will begin again to generate the next value.
Building a fuzzy controller
Consider implementing with a microcontroller chip a simple feedback controller:A fuzzy set is defined for the input error variable "e", and the derived change in error, "delta", as well as the "output", as follows:
LP: large positive
SP: small positive
ZE: zero
SN: small negative
LN: large negative
If the error ranges from -1 to +1, with the analog-to-digital converter used having a resolution of 0.25, then the input variable's fuzzy set (which, in this case, also applies to the output variable) can be described very simply as a table, with the error / delta / output values in the top row and the truth values for each membership function arranged in rows beneath:
_______________________________________________________________________
-1 -0.75 -0.5 -0.25 0 0.25 0.5 0.75 1
_______________________________________________________________________
mu(LP) 0 0 0 0 0 0 0.3 0.7 1
mu(SP) 0 0 0 0 0.3 0.7 1 0.7 0.3
mu(ZE) 0 0 0.3 0.7 1 0.7 0.3 0 0
mu(SN) 0.3 0.7 1 0.7 0.3 0 0 0 0
mu(LN) 1 0.7 0.3 0 0 0 0 0 0
_______________________________________________________________________—or, in graphical form (where each "X" has a value of 0.1):
LN SN ZE SP LP
+------------------------------------------------------------------+
| |
-1.0 | XXXXXXXXXX XXX : : : |
-0.75 | XXXXXXX XXXXXXX : : : |
-0.5 | XXX XXXXXXXXXX XXX : : |
-0.25 | : XXXXXXX XXXXXXX : : |
0.0 | : XXX XXXXXXXXXX XXX : |
0.25 | : : XXXXXXX XXXXXXX : |
0.5 | : : XXX XXXXXXXXXX XXX |
0.75 | : : : XXXXXXX XXXXXXX |
1.0 | : : : XXX XXXXXXXXXX |
| |
+------------------------------------------------------------------+
Suppose this fuzzy system has the following rule base:
rule 1: IF e = ZE AND delta = ZE THEN output = ZE
rule 2: IF e = ZE AND delta = SP THEN output = SN
rule 3: IF e = SN AND delta = SN THEN output = LP
rule 4: IF e = LP OR delta = LP THEN output = LN
These rules are typical for control applications in that the antecedents consist of the logical combination of the error and error-delta signals, while the consequent is a control command output.
The rule outputs can be defuzzified using a discrete centroid computation:
SUM( I = 1 TO 4 OF ( mu(I) * output(I) ) ) / SUM( I = 1 TO 4 OF mu(I) )
Now, suppose that at a given time we have:
e = 0.25
delta = 0.5
Then this gives:
________________________
e delta
________________________
mu(LP) 0 0.3
mu(SP) 0.7 1
mu(ZE) 0.7 0.3
mu(SN) 0 0
mu(LN) 0 0
________________________
Plugging this into rule 1 gives:
rule 1: IF e = ZE AND delta = ZE THEN output = ZE
mu(1) = MIN( 0.7, 0.3 ) = 0.3
output(1) = 0
-- where:
- mu(1): Truth value of the result membership function for rule 1. In terms of a centroid calculation, this is the "mass" of this result for this discrete case.
- output(1): Value (for rule 1) where the result membership function (ZE) is maximum over the output variable fuzzy set range. That is, in terms of a centroid calculation, the location of the "center of mass" for this individual result. This value is independent of the value of "mu". It simply identifies the location of ZE along the output range.
The other rules give:
rule 2: IF e = ZE AND delta = SP THEN output = SN
mu(2) = MIN( 0.7, 1 ) = 0.7
output(2) = -0.5
rule 3: IF e = SN AND delta = SN THEN output = LP
mu(3) = MIN( 0.0, 0.0 ) = 0
output(3) = 1
rule 4: IF e = LP OR delta = LP THEN output = LN
mu(4) = MAX( 0.0, 0.3 ) = 0.3
output(4) = -1
The centroid computation yields:
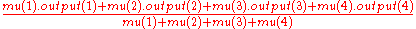
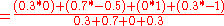
-- for the final control output. Simple. Of course the hard part is figuring out what rules actually work correctly in practice.
If you have problems figuring out the centroid equation, remember that a centroid is defined by summing all the moments (location times mass) around the center of gravity and equating the sum to zero. So if
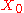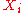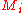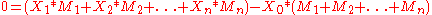
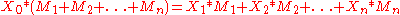
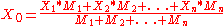
is the center of gravity, is the location of each mass, and is each mass, this gives:In our example, the values of mu correspond to the masses, and the values of X to location of the masses
(mu, however, only 'corresponds to the masses' if the initial 'mass' of the output functions are all the same/equivalent. If they are not the same, i.e. some are narrow triangles, while others maybe wide trapizoids or shouldered triangles, then the mass or area of the output function must be known or calculated. It is this mass that is then scaled by mu and multiplied by its location X_i).
This system can be implemented on a standard microprocessor, but dedicated fuzzy chips are now available. For example, Adaptive Logic INC of San Jose, California, sells a "fuzzy chip", the AL220, that can accept four analog inputs and generate four analog outputs. A block diagram of the chip is shown below:
+---------+ +-------+
analog --4-->| analog | | mux / +--4--> analog
in | mux | | SH | out
+----+----+ +-------+
| ^
V |
+-------------+ +--+--+
| ADC / latch | | DAC |
+------+------+ +-----+
| ^
| |
8 +-----------------------------+
| | |
| V |
| +-----------+ +-------------+ |
+-->| fuzzifier | | defuzzifier +--+
+-----+-----+ +-------------+
| ^
| +-------------+ |
| | rule | |
+->| processor +--+
| (50 rules) |
+------+------+
|
+------+------+
| parameter |
| memory |
| 256 x 8 |
+-------------+
ADC: analog-to-digital converter
DAC: digital-to-analog converter
SH: sample/hold
Antilock brakes
As a first example, consider an anti-lock braking systemAnti-lock braking system
An anti-lock braking system is a safety system that allows the wheels on a motor vehicle to continue interacting tractively with the road surface as directed by driver steering inputs while braking, preventing the wheels from locking up and therefore avoiding skidding.An ABS generally offers...
, directed by a microcontroller chip. The microcontroller has to make decisions based on brake temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
, and other variables in the system.
The variable "temperature" in this system can be subdivided into a range of "states": "cold", "cool", "moderate", "warm", "hot", "very hot". The transition from one state to the next is hard to define.
An arbitrary static threshold might be set to divide "warm" from "hot". For example, at exactly 90 degrees, warm ends and hot begins. But this would result in a discontinuous change when the input value passed over that threshold. The transition wouldn't be smooth, as would be required in braking situations.
The way around this is to make the states fuzzy. That is, allow them to change gradually from one state to the next. In order to do this there must be a dynamic relationship established between different factors.
We start by defining the input temperature states using "membership functions":
With this scheme, the input variable's state no longer jumps abruptly from one state to the next. Instead, as the temperature changes, it loses value in one membership function while gaining value in the next. In other words, its ranking in the category of cold decreases as it becomes more highly ranked in the warmer category.
At any sampled timeframe, the "truth value" of the brake temperature will almost always be in some degree part of two membership functions: i.e.: '0.6 nominal and 0.4 warm', or '0.7 nominal and 0.3 cool', and so on.
The above example demonstrates a simple application, using the abstraction
Abstraction
Abstraction is a process by which higher concepts are derived from the usage and classification of literal concepts, first principles, or other methods....
of values from multiple values. This only represents one kind of data, however, in this case, temperature.
Adding additional sophistication to this braking system, could be done by additional factors such as traction
Traction
- Engineering :*Forces:** Traction , adhesive friction or force in the context of vehicle** Traction vector, in mechanics, the force per unit area on a surface, including normal and shear components...
, speed, inertia
Inertia
Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...
, set up in dynamic functions, according to the designed fuzzy system.
Logical interpretation of fuzzy control
In spite of the appearance there are several difficulties to give a rigorous logical interpretation of the IF-THEN rules. As an example, interpret a rule as IF (temperature is "cold") THEN (heater is "high") by the first order formula Cold(x)→High(y) and assume that r is an input such that Cold(r) is false. Then the formula Cold(r)→High(t) is true for any t and therefore any t gives a correct control given r. Obviously, if we consider systems of rules in which the class antecedent define a partition such a paradoxical phenomenon does not arise. In any case there is sometime of unsatisfactory in considering two variables x and y in a rule without some kind of functional dependence. A rigorous logical justification of fuzzy control is given in Hájek's book (see Chapter 7) where fuzzy control is represented as a theory of Hájek's basic logic. Also in Gerla 2005 a logical approach to fuzzy control is proposed based on the following idea. Denote by f the fuzzy function associated with the fuzzy control system, i.e., given the input r, s(y) = f(r,y) is the fuzzy set of possible outputs. Then given a possible output 't', we interpret f(r,t) as the truth degree of the claim "t is a good answer given r". More formally, any system of IF-THEN rules can be translate into a fuzzy program in such a way that the fuzzy function f is the interpretation of a vague predicate Good(x,y) in the associated least fuzzy Herbrand model. In such a way fuzzy control becomes a chapter of fuzzy logic programming. The learning process becomes a question belonging to inductive logic theory.See also
- Dynamic logicDynamic logicDynamic logic may mean:* In theoretical computer science, dynamic logic is a modal logic for reasoning about dynamic behaviour* In digital electronics, dynamic logic is a technique used for combinatorial circuit design* A different concept proposed by Leonid Perlovsky...
- Bayesian inferenceBayesian inferenceIn statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
- Function approximationFunction approximationThe need for function approximations arises in many branches of applied mathematics, and computer science in particular. In general, a function approximation problem asks us to select a function among a well-defined class that closely matches a target function in a task-specific way.One can...
- Neural networksNeural NetworksNeural Networks is the official journal of the three oldest societies dedicated to research in neural networks: International Neural Network Society, European Neural Network Society and Japanese Neural Network Society, published by Elsevier...
- Neuro-fuzzyNeuro-fuzzyIn the field of artificial intelligence, neuro-fuzzy refers to combinations of artificial neural networks and fuzzy logic. Neuro-fuzzy was proposed by J. S. R. Jang...
- Fuzzy control languageFuzzy Control LanguageFuzzy Control Language, or FCL, is a language for implementing fuzzy logic, especially fuzzy control. It was standardized by IEC 61131-7. It is a domain-specific programming language: it has no features unrelated to fuzzy logic, so it is impossible to even print "Hello, world!"...
- Type-2 fuzzy sets and systemsType-2 fuzzy sets and systemsType-2 fuzzy sets and systems generalize fuzzy sets and systems so that more uncertainty can be handled. From the very beginning of fuzzy sets, criticism was made about the fact that the membership function of a type-1 fuzzy set has no uncertainty associated with it, something that seems to...
Further reading
- Kevin M. Passino and Stephen Yurkovich, Fuzzy Control, Addison Wesley Longman, Menlo Park, CA, 1998 (522 pages)
- Cox, E. (Oct. 1992). Fuzzy fundamentals. Spectrum, IEEE, 29:10. pp. 58–61.
- Cox, E. (Feb. 1993) Adaptive fuzzy systems. Spectrum, IEEE, 30:2. pp. 7–31.
- Jan Jantzen, "Tuning Of Fuzzy PID Controllers", Technical University of Denmark, report 98-H 871, September 30, 1998. http://www.iau.dtu.dk/~jj/pubs/fpid.pdf
- Jan Jantzen, Foundations of Fuzzy Control. Wiley, 2007 (209 pages) (Table of contents)