Fundamental theorem of linear algebra
Encyclopedia
In mathematics
, the fundamental theorem
of linear algebra
makes several statements regarding vector space
s. These may be stated concretely in terms of the rank
r of an m×n matrix
A and its singular value decomposition
:
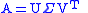
First, each matrix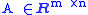 (
( has
has  rows and
rows and  columns) induces four fundamental subspaces
columns) induces four fundamental subspaces
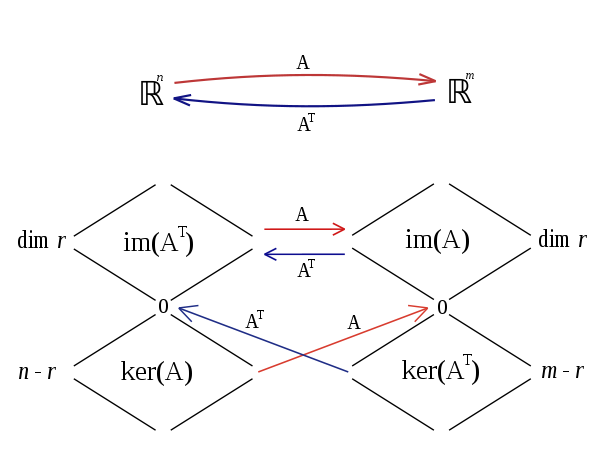
. These fundamental subspaces are:
Secondly:
 The dimensions of the subspaces are related by the rank–nullity theorem, and follow from the above theorem.
The dimensions of the subspaces are related by the rank–nullity theorem, and follow from the above theorem.
Further, all these spaces are intrinsically defined – they do not require a choice of basis – in which case one rewrites this in terms of abstract vector spaces, operators, and the dual space
s as and
and 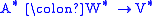 : the kernel and image of
: the kernel and image of 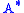 are the cokernel and coimage of
are the cokernel and coimage of  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the fundamental theorem
Fundamental theorem
The fundamental theorem of a field of mathematics is the theorem considered central to that field. The naming of such a theorem is not necessarily based on how often it is used or the difficulty of its proofs....
of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
makes several statements regarding vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s. These may be stated concretely in terms of the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
r of an m×n matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A and its singular value decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
:
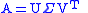
First, each matrix
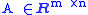 (
( has
has  rows and
rows and  columns) induces four fundamental subspaces
columns) induces four fundamental subspacesLinear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
. These fundamental subspaces are:
| name of subspace | definition | containing space | dimension | basis Basis (linear algebra) In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"... |
|---|---|---|---|---|
| column space Column space In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space... , range or image Image (mathematics) In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function... | 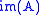 or or 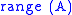 | 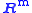 |  (rank (rankRank (linear algebra) The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A... ) | The first  columns of columns of  |
| nullspace or kernel Kernel (mathematics) In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix... | 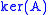 or or 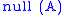 | 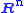 |  (nullity) (nullity) | The last  columns of columns of  |
| row space Row space In linear algebra, the row space of a matrix is the set of all possible linear combinations of its row vectors. The row space of an m × n matrix is a subspace of n-dimensional Euclidean space... or coimage Coimage In algebra, the coimage of a homomorphismis the quotientof domain and kernel.The coimage is canonically isomorphic to the image by the first isomorphism theorem, when that theorem applies.... | 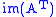 or or 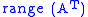 | 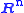 |  | The first  rows of rows of 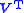 |
| left nullspace or cokernel Cokernel In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f.... | 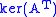 or or 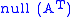 | 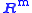 |  | The last  rows of rows of 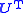 |
Secondly:
- In
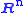 ,
,  , that is, the nullspace is the orthogonal complement of the row space
, that is, the nullspace is the orthogonal complement of the row space - In
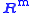 ,
,  , that is, the left nullspace is the orthogonal complement of the column space.
, that is, the left nullspace is the orthogonal complement of the column space.

Further, all these spaces are intrinsically defined – they do not require a choice of basis – in which case one rewrites this in terms of abstract vector spaces, operators, and the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
s as
 and
and 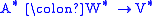 : the kernel and image of
: the kernel and image of 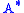 are the cokernel and coimage of
are the cokernel and coimage of  .
.External links
, MIT Linear Algebra Lecture on the Four Fundamental Subspaces at Google Video, from MIT OpenCourseWareMIT OpenCourseWare
MIT OpenCourseWare is an initiative of the Massachusetts Institute of Technology to put all of the educational materials from its undergraduate- and graduate-level courses online, partly free and openly available to anyone, anywhere. MIT OpenCourseWare is a large-scale, web-based publication of...

