
Essentially finite vector bundle
Encyclopedia
In mathematics, an essentially finite vector bundle is a particular type of vector bundle
defined by Madhav Nori, as the main tool in the construction of the fundamental group scheme
. Even if the definition is not intuitive there is a nice characterization that makes essentially finite vector bundles quite natural objects to study in algebraic geometry
. So before recalling the definition we give this characterization:
 be a reduced and connected scheme
be a reduced and connected scheme
over a perfect field
 endowed with a section
endowed with a section 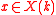 . Then a vector bundle
. Then a vector bundle 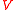 over
over  is essentially finite if and only if there exists a finite
is essentially finite if and only if there exists a finite  -group scheme
-group scheme
 and a
and a  -torsor
-torsor 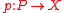 such that
such that 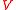 becomes trivial over
becomes trivial over  (i.e.
(i.e.  , where
, where 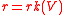 ).
).
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
defined by Madhav Nori, as the main tool in the construction of the fundamental group scheme
Fundamental group scheme
In mathematics, the fundamental group scheme is a group scheme canonically associated to a scheme over a Dedekind scheme . It is a generalisation of the étale fundamental group...
. Even if the definition is not intuitive there is a nice characterization that makes essentially finite vector bundles quite natural objects to study in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. So before recalling the definition we give this characterization:
Characterization
Let be a reduced and connected scheme
be a reduced and connected schemeScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
over a perfect field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
 endowed with a section
endowed with a section 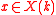 . Then a vector bundle
. Then a vector bundle 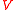 over
over  is essentially finite if and only if there exists a finite
is essentially finite if and only if there exists a finite  -group scheme
-group schemeGroup scheme
In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...
 and a
and a  -torsor
-torsor 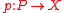 such that
such that 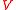 becomes trivial over
becomes trivial over  (i.e.
(i.e.  , where
, where 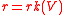 ).
).

