Friendly number
Encyclopedia
In number theory
, friendly numbers are two or more natural numbers
with a common abundancy, the ratio between the sum of divisor
s of a number and the number itself. Two numbers with the same abundancy form a friendly pair; n numbers with the same abundancy form a friendly n-tuple.
Being mutually friendly is an equivalence relation
, and thus induces a partition of the positive naturals into clubs (equivalence classes) of mutually friendly numbers.
A number that is not part of any friendly pair is called solitary.
The abundancy of n is the rational number
σ(n) / n, in which σ denotes the sum of divisors function
. A number n is a friendly number if there exists m ≠ n such that σ(m) / m = σ(n) / n. Note that abundancy is not the same as abundance which is defined as σ(n) − 2n.
Abundancy may also be expressed as
where 
denotes a divisor function with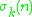 
equal to the sum of the k-th powers of the divisors of n.
The numbers 1 through 5 are all solitary. The smallest friendly number is 6, forming for example the friendly pair (6, 28) with abundancy σ(6) / 6 = (1+2+3+6) / 6 = 2, the same as σ(28) / 28 = (1+2+4+7+14+28) / 28 = 2. The shared value 2 is an integer in this case but not in many other cases. There are several unsolved problems related to the friendly numbers.
In spite of the similarity in name, there is no specific relationship between the friendly numbers and the amicable number
s or the sociable number
s, although the definitions of the latter two also involve the divisor function.
The numbers 2480, 6200 and 40640 are also members of this club, as they each have an abundancy equal to 12/5.
– meaning that the greatest common divisor
of these numbers is 1, so that σ(n)/n is an irreducible fraction – then the number n is solitary. For a prime number p we have σ(p) = p + 1, which is coprime with p.
No general method is known for determining whether a number is friendly or solitary. The smallest number whose classification is unknown (as of 2009) is 10; it is conjectured to be solitary; if not, its smallest friend is a fairly large number.
s), but no proof is known. As of June 2009, 47 perfect numbers are known, the largest of which has more than 25 million digits in decimal
notation. There are clubs with more known members, in particular those formed by multiply perfect number
s, which are numbers whose abundancy is an integer. As of early 2008, the club of friendly numbers with abundancy equal to 9 has 2079 known members. Although some are known to be quite large, clubs of multiply perfect numbers (excluding the perfect numbers themselves) are conjectured to be finite.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, friendly numbers are two or more natural numbers
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
with a common abundancy, the ratio between the sum of divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s of a number and the number itself. Two numbers with the same abundancy form a friendly pair; n numbers with the same abundancy form a friendly n-tuple.
Being mutually friendly is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, and thus induces a partition of the positive naturals into clubs (equivalence classes) of mutually friendly numbers.
A number that is not part of any friendly pair is called solitary.
The abundancy of n is the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
σ(n) / n, in which σ denotes the sum of divisors function
Divisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
. A number n is a friendly number if there exists m ≠ n such that σ(m) / m = σ(n) / n. Note that abundancy is not the same as abundance which is defined as σ(n) − 2n.
Abundancy may also be expressed as
where 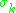denotes a divisor function with 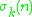equal to the sum of the k-th powers of the divisors of n.The numbers 1 through 5 are all solitary. The smallest friendly number is 6, forming for example the friendly pair (6, 28) with abundancy σ(6) / 6 = (1+2+3+6) / 6 = 2, the same as σ(28) / 28 = (1+2+4+7+14+28) / 28 = 2. The shared value 2 is an integer in this case but not in many other cases. There are several unsolved problems related to the friendly numbers.
In spite of the similarity in name, there is no specific relationship between the friendly numbers and the amicable number
Amicable number
Amicable numbers are two different numbers so related that the sum of the proper divisors of each is equal to the other number. A pair of amicable numbers constitutes an aliquot sequence of period 2...
s or the sociable number
Sociable number
Sociable numbers are generalizations of the concepts of amicable numbers and perfect numbers. A set of sociable numbers is a kind of aliquot sequence, or a sequence of numbers each of whose numbers is the sum of the factors of the preceding number, excluding the preceding number itself...
s, although the definitions of the latter two also involve the divisor function.
Example
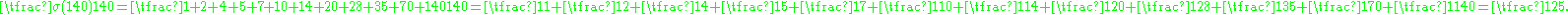
As another example, (30, 140) is a friendly pair, because 30 and 140 have the same abundancy:The numbers 2480, 6200 and 40640 are also members of this club, as they each have an abundancy equal to 12/5.
Solitary numbers
A number that belongs to a singleton club, because no other number is friendly with it, is a solitary number. All prime numbers are known to be solitary, as are powers of prime numbers. More generally, if the numbers n and σ(n) are coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
– meaning that the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of these numbers is 1, so that σ(n)/n is an irreducible fraction – then the number n is solitary. For a prime number p we have σ(p) = p + 1, which is coprime with p.
No general method is known for determining whether a number is friendly or solitary. The smallest number whose classification is unknown (as of 2009) is 10; it is conjectured to be solitary; if not, its smallest friend is a fairly large number.
Large clubs
It is an open problem whether there are infinitely large clubs of mutually friendly numbers. The perfect numbers form a club, and it is conjectured that there are infinitely many perfect numbers (at least as many as there are Mersenne primeMersenne prime
In mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...
s), but no proof is known. As of June 2009, 47 perfect numbers are known, the largest of which has more than 25 million digits in decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
notation. There are clubs with more known members, in particular those formed by multiply perfect number
Multiply perfect number
In mathematics, a multiply perfect number is a generalization of a perfect number....
s, which are numbers whose abundancy is an integer. As of early 2008, the club of friendly numbers with abundancy equal to 9 has 2079 known members. Although some are known to be quite large, clubs of multiply perfect numbers (excluding the perfect numbers themselves) are conjectured to be finite.