
Four fours
Encyclopedia
Four fours is a mathematical puzzle
. The goal of four fours is to find the simplest mathematical expression for every whole number
from 0 to some maximum, using only common mathematical symbols and the digit four (no other digit is allowed). Most versions of four fours require that each expression have exactly four fours, but some variations require that each expression have the minimum number of fours.
("+"), subtraction
("−"), multiplication
("×"), division
("÷"), and parentheses
, as well as concatenation (e.g., "44" is allowed). Most also allow the factorial
("!"), exponentiation
(e.g. "444"), the decimal point (".") and the square root
operation, although sometimes square root is specifically excluded on the grounds that there is an implied "2" for the second root. Other operations allowed by some variations include subfactorial, ("!" before the number: !4 equals 9),
overline (an infinitely repeated digit), an arbitrary root power, the gamma function
(Γ, where Γ(x) = (x − 1)!),
and percent ("%"). Thus 4/4% = 100 and Γ(4)=6. A common use of the overline in this problem is for this value: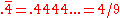
Typically the "log
" operators are not allowed, since there is a way to trivially create any number using them. Paul Bourke credits Ben Rudiak-Gould with this description of how natural logarithms (ln) can be used to represent any positive integer n as:
Additional variants (usually no longer called "four fours") replace the set of digits ("4, 4, 4, 4") with some other set of digits, say of the birthyear of someone. For example, a variant using "1975" would require each expression to use one 1, one 9, one 7, and one 5.
. Numbers without blue entries have no solution under these constraints.
0
1
2
3
4
5
6 4.4 + 4 ×.4
7 44 ÷ 4 − 4
8 4 +4.4−.4
9
10 (44 − 4)/ 4 44 ÷ 4.4
11
12 (44 + 4)÷ 4
13 4!−44 ÷ 4 (4 −.4)÷.4 + 4
14 4 ×(4 −.4)−.4 4 ÷.4 +√4 +√4 4 + 4 + 4 +√4
15
16 (44 − 4)×.4
17
18 4 × 4 + 4 ÷√4
19 4!− 4 −(4 ÷ 4)
20
There are also many other ways to find the answer for all of these.
Note that numbers with values less than one are not usually written with a leading zero. For example, "0.4" is usually written as ".4". This is because "0" is a digit, and in this puzzle only the digit "4" can be used.
A given number will generally have few possible solutions; any solution that meets the rules is acceptable. Some variations prefer the "fewest" number of operations, or prefer some operations to others. Others simply prefer "interesting" solutions, i.e., a surprising way to reach the goal.
Certain numbers, such as 113 and 123, are particularly difficult to solve under typical rules. For 113, Wheeler suggests Γ(Γ(4)) −(4! + 4)/4. For 123, Wheeler suggests the expression:

The first printed occurrence of this activity is in "Mathematical Recreations and Essays" by W. W. Rouse Ball
published in 1892. In this book it is described as a "traditional recreation".
s that map rationals to strings. In these tables, the keys are the numbers being represented by some admissible combination of operators and the chosen digit d, e.g. four, and the values are strings that contain the actual formula. There is one table for each number n of occurrences of d. For example, when d=4, the hash table for two occurrences of d would contain the key-value pair 8 and 4+4, and the one for three occurrences, the key-value pair 2 and (4+4)/4 (strings shown in bold).
The task is then reduced to recursively computing these hash tables for increasing n, starting from n=1 and continuing up to e.g. n=4. The tables for n=1 and n=2 are special, because they contain primitive entries that are not the combination of other, smaller formulas, and hence they must be initialized properly, like so (for n=1)
T[4] := "4";
T[4/10] := ".4";
T[4/9] := ".4...";
and
T[44] := "44";.
(for n=2). Now there are two ways in which new entries may arise, either as a combination of existing ones through a binary operator, or by applying the factorial or square root operators (which does not use additional instances of d). The first case is treated by iterating over all pairs of subexpressions that use a total of n instances of d. For example, when n=4, we would check pairs (a,b) with a containing one instance of d and b three, and with a containing two instances of d and b two as well. We would then enter a+b, a-b, b-a, a*b, a/b, b/a) into the hash table, including parenthesis, for n=4. Here the sets A and B that contain a and b are calculated recursively, with n=1 and n=2 being the base case. Memoization
is used to ensure that every hash table is only computed once.
The second case (factorials and roots) is treated with the help of an auxiliary function, which is invoked every time a value v is recorded. This function computes nested factorials and roots of v up to some maximum depth, restricted to rationals.
The last phase of the algorithm consists in iterating over the keys of the table for the desired value of n and extracting and sorting those keys that are integers. This algorithm was used to calculate the five fives and six sixes examples shown below. The more compact formula (in the sense of number of characters in the corresponding value) was chosen every time a key occurred more than once.
140 = (.5*(5+(5*55)))
141 = ((5)!+((5+(5+.5))/.5))
142 = ((5)!+((55/.5)/5))
143 = ((((5+(5/5)))!-5)/5)
144 = ((((55/5)-5))!/5)
145 = ((5*(5+(5*5)))-5)
146 = ((5)!+((5/5)+(5*5)))
147 = ((5)!+((.5*55)-.5))
148 = ((5)!+(.5+(.5*55)))
149 = (5+(((5+(5/5)))!/5))
241 = ((.6+((6+6)*(6+6)))/.6)
242 = ((6*(6+(6*6)))-(6/.6))
243 = (6+((6*(.6*66))-.6))
244 = (.6...*(6+(6*(66-6))))
245 = ((((6)!+((6)!+66))/6)-6)
246 = (66+(6*((6*6)-6)))
247 = (66+((6+((6)!/.6...))/6))
248 = (6*(6+(6*(6-(.6.../6)))))
249 = (.6+(6*(6+((6*6)-.6))))
250 = (((6*(6*6))-66)/.6)
251 = ((6*(6+(6*6)))-(6/6))
252 = (66+(66+((6)!/6)))
253 = ((6/6)+(6*(6+(6*6))))
254 = ((.6...*((6*66)-6))-6)
255 = ((((6*6)+66)/.6)/.6...)
256 = (6*(6*(6-(6/(.6-6)))))
257 = (6+(((6)!+((6)!+66))/6))
258 = ((6)!-(66+(6*66)))
259 = ((((6*6)+((6)!/6))-.6)/.6)
260 = ((66+(((6)!/.6)/6))-6)
Mathematical puzzle
Mathematical puzzles make up an integral part of recreational mathematics. They have specific rules as do multiplayer games, but they do not usually involve competition between two or more players. Instead, to solve such a puzzle, the solver must find a solution that satisfies the given conditions....
. The goal of four fours is to find the simplest mathematical expression for every whole number
Whole number
Whole number is a term with inconsistent definitions by different authors. All distinguish whole numbers from fractions and numbers with fractional parts.Whole numbers may refer to:*natural numbers in sense — the positive integers...
from 0 to some maximum, using only common mathematical symbols and the digit four (no other digit is allowed). Most versions of four fours require that each expression have exactly four fours, but some variations require that each expression have the minimum number of fours.
Rules
There are many variations of four fours; their primary difference is which mathematical symbols are allowed. Essentially all variations at least allow additionAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
("+"), subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
("−"), multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
("×"), division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
("÷"), and parentheses
Bracket
Brackets are tall punctuation marks used in matched pairs within text, to set apart or interject other text. In the United States, "bracket" usually refers specifically to the "square" or "box" type.-List of types:...
, as well as concatenation (e.g., "44" is allowed). Most also allow the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
("!"), exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
(e.g. "444"), the decimal point (".") and the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
operation, although sometimes square root is specifically excluded on the grounds that there is an implied "2" for the second root. Other operations allowed by some variations include subfactorial, ("!" before the number: !4 equals 9),
overline (an infinitely repeated digit), an arbitrary root power, the gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
(Γ, where Γ(x) = (x − 1)!),
and percent ("%"). Thus 4/4% = 100 and Γ(4)=6. A common use of the overline in this problem is for this value:
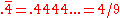
Typically the "log
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
" operators are not allowed, since there is a way to trivially create any number using them. Paul Bourke credits Ben Rudiak-Gould with this description of how natural logarithms (ln) can be used to represent any positive integer n as:

Additional variants (usually no longer called "four fours") replace the set of digits ("4, 4, 4, 4") with some other set of digits, say of the birthyear of someone. For example, a variant using "1975" would require each expression to use one 1, one 9, one 7, and one 5.
Solutions
Here is a set of four fours solutions for the numbers 0 through 20, using typical rules. Some alternate solutions are listed here, although there are actually many more correct solutions. The entries in blue are those that use four integers 4 (rather than four digits 4) and the basic arithmetic operationsElementary arithmetic
Elementary arithmetic is the simplified portion of arithmetic which is considered necessary and appropriate during primary education. It includes the operations of addition, subtraction, multiplication, and division. It is taught in elementary school....
. Numbers without blue entries have no solution under these constraints.
0
1
2
3
4
5
6 4.4 + 4 ×.4
7 44 ÷ 4 − 4
8 4 +4.4−.4
9
10 (44 − 4)/ 4 44 ÷ 4.4
11
12 (44 + 4)÷ 4
13 4!−44 ÷ 4 (4 −.4)÷.4 + 4
14 4 ×(4 −.4)−.4 4 ÷.4 +√4 +√4 4 + 4 + 4 +√4
15
16 (44 − 4)×.4
17
18 4 × 4 + 4 ÷√4
19 4!− 4 −(4 ÷ 4)
20
There are also many other ways to find the answer for all of these.
Note that numbers with values less than one are not usually written with a leading zero. For example, "0.4" is usually written as ".4". This is because "0" is a digit, and in this puzzle only the digit "4" can be used.
A given number will generally have few possible solutions; any solution that meets the rules is acceptable. Some variations prefer the "fewest" number of operations, or prefer some operations to others. Others simply prefer "interesting" solutions, i.e., a surprising way to reach the goal.
Certain numbers, such as 113 and 123, are particularly difficult to solve under typical rules. For 113, Wheeler suggests Γ(Γ(4)) −(4! + 4)/4. For 123, Wheeler suggests the expression:

The first printed occurrence of this activity is in "Mathematical Recreations and Essays" by W. W. Rouse Ball
W. W. Rouse Ball
-External links:*...
published in 1892. In this book it is described as a "traditional recreation".
Algorithmics of the problem
This problem and its generalizations (like the five fives and the six sixes problem, both shown below) may be solved by a simple algorithm. The basic ingredients are hash tableHash table
In computer science, a hash table or hash map is a data structure that uses a hash function to map identifying values, known as keys , to their associated values . Thus, a hash table implements an associative array...
s that map rationals to strings. In these tables, the keys are the numbers being represented by some admissible combination of operators and the chosen digit d, e.g. four, and the values are strings that contain the actual formula. There is one table for each number n of occurrences of d. For example, when d=4, the hash table for two occurrences of d would contain the key-value pair 8 and 4+4, and the one for three occurrences, the key-value pair 2 and (4+4)/4 (strings shown in bold).
The task is then reduced to recursively computing these hash tables for increasing n, starting from n=1 and continuing up to e.g. n=4. The tables for n=1 and n=2 are special, because they contain primitive entries that are not the combination of other, smaller formulas, and hence they must be initialized properly, like so (for n=1)
T[4] := "4";
T[4/10] := ".4";
T[4/9] := ".4...";
and
T[44] := "44";.
(for n=2). Now there are two ways in which new entries may arise, either as a combination of existing ones through a binary operator, or by applying the factorial or square root operators (which does not use additional instances of d). The first case is treated by iterating over all pairs of subexpressions that use a total of n instances of d. For example, when n=4, we would check pairs (a,b) with a containing one instance of d and b three, and with a containing two instances of d and b two as well. We would then enter a+b, a-b, b-a, a*b, a/b, b/a) into the hash table, including parenthesis, for n=4. Here the sets A and B that contain a and b are calculated recursively, with n=1 and n=2 being the base case. Memoization
Memoization
In computing, memoization is an optimization technique used primarily to speed up computer programs by having function calls avoid repeating the calculation of results for previously processed inputs...
is used to ensure that every hash table is only computed once.
The second case (factorials and roots) is treated with the help of an auxiliary function, which is invoked every time a value v is recorded. This function computes nested factorials and roots of v up to some maximum depth, restricted to rationals.
The last phase of the algorithm consists in iterating over the keys of the table for the desired value of n and extracting and sorting those keys that are integers. This algorithm was used to calculate the five fives and six sixes examples shown below. The more compact formula (in the sense of number of characters in the corresponding value) was chosen every time a key occurred more than once.
Excerpt from the solution to the five fives problem
139 = ((((5+(5/5)))!/5)-5)140 = (.5*(5+(5*55)))
141 = ((5)!+((5+(5+.5))/.5))
142 = ((5)!+((55/.5)/5))
143 = ((((5+(5/5)))!-5)/5)
144 = ((((55/5)-5))!/5)
145 = ((5*(5+(5*5)))-5)
146 = ((5)!+((5/5)+(5*5)))
147 = ((5)!+((.5*55)-.5))
148 = ((5)!+(.5+(.5*55)))
149 = (5+(((5+(5/5)))!/5))
Excerpt from the solution to the six sixes problem
In the table below, the notation .6... represents the value 6/9 or 2/3 (recurring decimal 6).241 = ((.6+((6+6)*(6+6)))/.6)
242 = ((6*(6+(6*6)))-(6/.6))
243 = (6+((6*(.6*66))-.6))
244 = (.6...*(6+(6*(66-6))))
245 = ((((6)!+((6)!+66))/6)-6)
246 = (66+(6*((6*6)-6)))
247 = (66+((6+((6)!/.6...))/6))
248 = (6*(6+(6*(6-(.6.../6)))))
249 = (.6+(6*(6+((6*6)-.6))))
250 = (((6*(6*6))-66)/.6)
251 = ((6*(6+(6*6)))-(6/6))
252 = (66+(66+((6)!/6)))
253 = ((6/6)+(6*(6+(6*6))))
254 = ((.6...*((6*66)-6))-6)
255 = ((((6*6)+66)/.6)/.6...)
256 = (6*(6*(6-(6/(.6-6)))))
257 = (6+(((6)!+((6)!+66))/6))
258 = ((6)!-(66+(6*66)))
259 = ((((6*6)+((6)!/6))-.6)/.6)
260 = ((66+(((6)!/.6)/6))-6)

