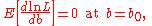Fisher consistency
Encyclopedia
In statistics
, Fisher consistency, named after Ronald Fisher
, is a desirable property of an estimator
asserting that if the estimator were calculated using the entire population
rather than a sample
, the true value of the estimated parameter would be obtained.
X1, ..., Xn where each Xi follows a cumulative distribution Fθ which depends on an unknown parameter
θ. If an estimator of θ based on the sample can be represented as a functional
of the empirical distribution function
F̂n:
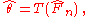
the estimator is said to be Fisher consistent if:
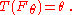
As long as the Xi are exchangeable, an estimator T defined in terms of the Xi can be converted into an estimator T′ that can be defined in terms of F̂n by averaging T over all permutations of the data. The resulting estimator will have the same expected value as T and its variance will be no larger than that of T.
If the strong law of large numbers can be applied, the empirical distribution functions F̂n converge pointwise to Fθ, allowing us to express Fisher consistency as a limit — the estimator is Fisher consistent if
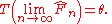
Suppose the parameter of interest is the expected value
μ and the estimator is the sample mean
, which can be written
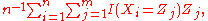
where I is the indicator function. The population analogue of this expression is
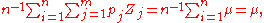
so we have Fisher consistency.
where b0 represents the true value of b.
. Fisher consistency and asymptotic consistency are distinct concepts, although both aim to define a desirable property of an estimator. While many estimators are consistent in both senses, neither definition encompasses the other. For example, suppose we take an estimator Tn that is both Fisher consistent and asymptotically consistent, and then form Tn + En, where En is a deterministic sequence of nonzero numbers converging to zero. This estimator is asymptotically consistent, but not Fisher consistent for any n. Alternatively, take a sequence of Fisher consistent estimators Sn, then define Tn = Sn for n < n0, and Tn = Sn0 for all n ≥n0. This estimator is Fisher consistent for all n, but not asymptotically consistent. A concrete example of this construction would be estimating the population mean as X1 regardless of the sample size.
The sample mean is a Fisher consistent and unbiased
estimate of the population mean, but not all Fisher consistent estimates are unbiased. Suppose we observe a sample from a uniform distribution
on (0,θ) and we wish to estimate θ. The sample maximum is Fisher consistent, but downwardly biased. Conversely, the sample variance is an unbiased estimate of the population variance, but is not Fisher consistent.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Fisher consistency, named after Ronald Fisher
Ronald Fisher
Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...
, is a desirable property of an estimator
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
asserting that if the estimator were calculated using the entire population
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
rather than a sample
Sample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
, the true value of the estimated parameter would be obtained.
Definition
Suppose we have a statistical sampleSample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
X1, ..., Xn where each Xi follows a cumulative distribution Fθ which depends on an unknown parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
θ. If an estimator of θ based on the sample can be represented as a functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
of the empirical distribution function
Empirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
F̂n:
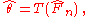
the estimator is said to be Fisher consistent if:
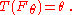
As long as the Xi are exchangeable, an estimator T defined in terms of the Xi can be converted into an estimator T′ that can be defined in terms of F̂n by averaging T over all permutations of the data. The resulting estimator will have the same expected value as T and its variance will be no larger than that of T.
If the strong law of large numbers can be applied, the empirical distribution functions F̂n converge pointwise to Fθ, allowing us to express Fisher consistency as a limit — the estimator is Fisher consistent if
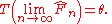
Finite population example
Suppose our sample is obtained from a finite population Z1, ..., Zm. We can represent our sample of size n in terms of the proportion of the sample ni / n taking on each value in the population. Writing our estimator of θ as T(n1 / n, ..., nm / n), the population analogue of the estimator is T(p1, ..., pm), where pi = P(X = Zi). Thus we have Fisher consistency if T(p1, ..., pm) = θ.Suppose the parameter of interest is the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
μ and the estimator is the sample mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
, which can be written
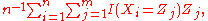
where I is the indicator function. The population analogue of this expression is
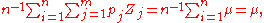
so we have Fisher consistency.
Role in maximum likelihood estimation
Maximising the likelihood function L gives an estimate that is Fisher consistent for a parameter b ifwhere b0 represents the true value of b.
Relationship to asymptotic consistency and unbiasedness
The term consistency in statistics usually refers to an estimator that is asymptotically consistentConsistent estimator
In statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...
. Fisher consistency and asymptotic consistency are distinct concepts, although both aim to define a desirable property of an estimator. While many estimators are consistent in both senses, neither definition encompasses the other. For example, suppose we take an estimator Tn that is both Fisher consistent and asymptotically consistent, and then form Tn + En, where En is a deterministic sequence of nonzero numbers converging to zero. This estimator is asymptotically consistent, but not Fisher consistent for any n. Alternatively, take a sequence of Fisher consistent estimators Sn, then define Tn = Sn for n < n0, and Tn = Sn0 for all n ≥n0. This estimator is Fisher consistent for all n, but not asymptotically consistent. A concrete example of this construction would be estimating the population mean as X1 regardless of the sample size.
The sample mean is a Fisher consistent and unbiased
Bias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
estimate of the population mean, but not all Fisher consistent estimates are unbiased. Suppose we observe a sample from a uniform distribution
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on (0,θ) and we wish to estimate θ. The sample maximum is Fisher consistent, but downwardly biased. Conversely, the sample variance is an unbiased estimate of the population variance, but is not Fisher consistent.