
Fatou–Lebesgue theorem
Encyclopedia
In mathematics
, the Fatou–Lebesgue theorem establishes a chain of inequalities relating the integral
s (in the sense of Lebesgue
) of the limit inferior
and the limit superior
of a sequence
of function
s to the limit inferior and the limit superior of integrals of these functions. The theorem is named after Pierre Fatou
and Henri Léon Lebesgue.
If the sequence of functions converges pointwise
, the inequalities turn into equalities and the theorem reduces to Lebesgue's dominated convergence theorem
.
-valued measurable
functions defined on a measure space (S,Σ,μ). If there exists a Lebesgue-integrable function g on S which dominates the sequence in absolute value, meaning that |fn| ≤ g for all natural number
s n, then all fn as well as the limit inferior and the limit superior of the fn are integrable and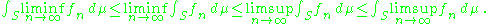
Here the limit inferior and the limit superior of the fn are taken pointwise. The integral of the absolute value of these limiting functions is bounded above by the integral of g.
Since the middle inequality (for sequences of real numbers) is always true, the directions of the other inequalities are easy to remember.
The first inequality follows by applying Fatou's lemma
to the non-negative functions fn + g and using the linearity of the Lebesgue integral. The last inequality is the reverse Fatou lemma.
Since g also dominates the limit superior of the |fn|,
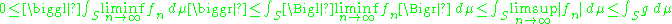
by the monotonicity of the Lebesgue integral. The same estimates hold for the limit superior of the fn.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Fatou–Lebesgue theorem establishes a chain of inequalities relating the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s (in the sense of Lebesgue
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
) of the limit inferior
Limit superior and limit inferior
In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence...
and the limit superior
Limit superior and limit inferior
In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence...
of a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s to the limit inferior and the limit superior of integrals of these functions. The theorem is named after Pierre Fatou
Pierre Fatou
Pierre Joseph Louis Fatou was a French mathematician working in the field of complex analytic dynamics. He entered the École Normale Supérieure in Paris in 1898 to study mathematics and graduated in 1901 when he was appointed an astronomy post in the Paris Observatory...
and Henri Léon Lebesgue.
If the sequence of functions converges pointwise
Pointwise convergence
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
, the inequalities turn into equalities and the theorem reduces to Lebesgue's dominated convergence theorem
Dominated convergence theorem
In measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
.
Statement of the theorem
Let f1, f2, ... denote a sequence of realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued measurable
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
functions defined on a measure space (S,Σ,μ). If there exists a Lebesgue-integrable function g on S which dominates the sequence in absolute value, meaning that |fn| ≤ g for all natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s n, then all fn as well as the limit inferior and the limit superior of the fn are integrable and
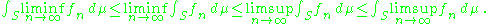
Here the limit inferior and the limit superior of the fn are taken pointwise. The integral of the absolute value of these limiting functions is bounded above by the integral of g.
Since the middle inequality (for sequences of real numbers) is always true, the directions of the other inequalities are easy to remember.
Proof
All fn as well as the limit inferior and the limit superior of the fn are measurable and dominated in absolute value by g, hence integrable.The first inequality follows by applying Fatou's lemma
Fatou's lemma
In mathematics, Fatou's lemma establishes an inequality relating the integral of the limit inferior of a sequence of functions to the limit inferior of integrals of these functions...
to the non-negative functions fn + g and using the linearity of the Lebesgue integral. The last inequality is the reverse Fatou lemma.
Since g also dominates the limit superior of the |fn|,
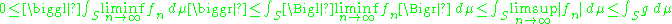
by the monotonicity of the Lebesgue integral. The same estimates hold for the limit superior of the fn.

