FKG inequality
Encyclopedia
The FKG inequality is a correlation
inequality, a fundamental tool in statistical mechanics
and probabilistic combinatorics (especially random graph
s and the probabilistic method
), due to . Informally, it says that in many random systems, increasing events are positively correlated, while an increasing and a decreasing event are negatively correlated.
An earlier version, for the special case of i.i.d. variables, is due to , see below. One generalization of the FKG inequality is the Holley inequality (1974) below, and an even further generalization is the Ahlswede-Daykin "four functions" theorem (1978). Furthermore, it has the same conclusion as the Griffiths inequalities, but the hypotheses are different.
be a finite distributive lattice
, and μ a positive function on it, that is assumed to satisfy the lattice condition, i.e.,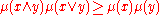
for all x, y in the lattice
.
For any function
, its expected value
with respect to μ is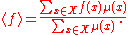
The FKG inequality then says that for any two monotonically increasing functions ƒ and g on
, the following positive correlation inequality holds:
The same inequality (positive correlation) is true when both ƒ and g are decreasing.
If one is increasing and the other is decreasing, then they are negatively correlated: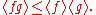
Similar statements hold more generally, when
is not necessarily finite, not even countable. In that case, μ has to be a finite measure, and the lattice condition has to be defined using cylinder events.
For proofs, see the original or the Ahlswede-Daykin inequality (1978). Also, a rough sketch is given below, due to , using a Markov chain
coupling
argument.
The property of μ that increasing functions are positively correlated is also called having positive associations, or the weak FKG condition.
Thus, the FKG theorem can be rephrased as "the strong FKG condition implies the weak FKG condition".
is totally ordered, then the lattice condition is satisfied trivially for any measure μ. For this case, the FKG inequality is Chebyshev's sum inequality
: if the two increasing functions take on values
and 
, then (we may assume that measure μ is uniform)
More generally, for any probability measure μ on
and increasing functions ƒ and g,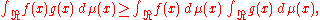
which follows immediately from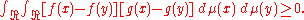
The lattice condition is trivially satisfied also when the lattice is the product of totally ordered lattices,
, and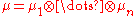 
is a product measure. Often all the factors (both the lattices and the measures) are identical, i.e., μ is the probability distribution of i.i.d. random variables.
The FKG (Chebyshev's sum) inequality for the case of a product measure is known also as the Harris inequality after Harris , who used it in his study of percolation
in the plane. The proof given above can be found, e.g., in .
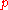and white with probability 
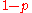, independently of each other. Let a, b, c, d be four hexagons, not necessarily distinct. Let 
and 
be the events that there is a black path from a to b, and a black path from c to d, respectively. Then the Harris inequality says that these events are positively correlated: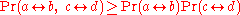 
. In other words, assuming the presence of one path can only increase the probability of the other.
Similarly, if we randomly color the hexagons inside an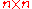
rhombus-shaped hex board
, then the events that there is black crossing from the left side of the board to the right side is positively correlated with having a black crossing from the top side to the bottom. On the other hand, having a left-to-right black crossing is negatively correlated with having a top-to-bottom white crossing, since the first is an increasing event (in the amount of blackness), while the second is decreasing. In fact, in any coloring of the hex board exactly one of these two events happen — this is why hex is a well-defined game.
In the Erdős-Rényi random graph, the existence of a Hamiltonian cycle is negatively correlated with the 3-colorability of the graph
, since the first is an increasing event, while the latter is decreasing.
If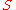
is an ordered set (such as 
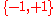), and 
is a finite or infinite graph
, then the set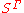
of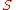 
-valued configurations is a poset that is a distributive lattice.
Now, if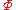
is a submodular potential
(i.e., a family of functions
one for each finite
, such that each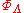 
is submodular), then one defines the corresponding Hamiltonian
s as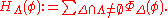
If μ is an extremal Gibbs measure
for this Hamiltonian on the set of configurations
, then it is easy to show that μ satisfies the lattice condition, see .
A key example is the Ising model
on a graph
. Let 
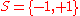, called spins, and 
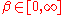. Take the following potential: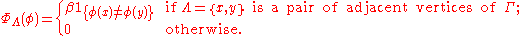
Submodularity is easy to check; intuitively, taking the min or the max of two configurations tends to decrease the number of disagreeing spins. Then, depending on the graph
and the value of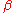 
, there could be one or more extremal Gibbs measures, see, e.g., and .
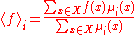
of a monotonically increasing function ƒ on a finite distributive lattice
with respect to two positive functions μ1, μ2 on the lattice satisfy the condition
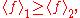
provided the functions satisfy
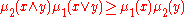
for all x, y in the lattice.
To get back the FKG inequality: If μ satisfies the lattice condition and ƒ and g are increasing functions on
, then μ1(x):=g(x)μ(x) and μ2(x):=μ(x) will satisfy the lattice-type condition of the Holley inequality. Then the Holley inequality says that
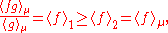
which is just the FKG inequality.
Similarly to FKG, the Holley inequality also follows from the Ahlswede–Daykin inequality
.
being a product 
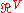for some finite set 
. The lattice condition on μ is easily seen to imply the following monotonicity, which has the virtue that it is often easier to check than the lattice condition:
Whenever one fixes a vertex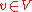
and two configurations φ and ψ outside v such that 
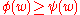for all 
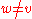, the μ-conditional distribution of φ(v) given 
stochastically dominates
the μ-conditional distribution of ψ(v) given
.
Now, if μ satisfies this monotonicity property, that is already enough for the FKG inequality (positive associations) to hold.
Here is a rough sketch of the proof, due to : starting from any initial configuration on
, one can run a simple Markov chain
(the Metropolis algorithm) that uses independent Uniform[0,1] random variables to update the configuration in each step, such that the chain has a unique stationary measure, the given μ. The monotonicity of μ implies that the configuration at each step is a monotone function of independent variables, hence the product measure version of Harris implies that it has positive associations. Therefore, the limiting stationary measure μ also has this property.
The monotonicity property has a natural version for two measures, saying that μ1 conditionally pointwise dominates μ2. It is again easy to see that if μ1 and μ2 satisfy the lattice-type condition of the Holley inequality, then μ1 conditionally pointwise dominates μ2. On the other hand, a Markov chain coupling
argument similar to the above, but now without invoking the Harris inequality, shows that conditional pointwise domination, in fact, implies stochastically domination
. Stochastic domination is equivalent to saying that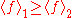
for all increasing ƒ, thus we get a proof of the Holley inequality. (And thus also a proof of the FKG inequality, without using the Harris inequality.)
See and for details.
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
inequality, a fundamental tool in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
and probabilistic combinatorics (especially random graph
Random graph
In mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
s and the probabilistic method
Probabilistic method
The probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
), due to . Informally, it says that in many random systems, increasing events are positively correlated, while an increasing and a decreasing event are negatively correlated.
An earlier version, for the special case of i.i.d. variables, is due to , see below. One generalization of the FKG inequality is the Holley inequality (1974) below, and an even further generalization is the Ahlswede-Daykin "four functions" theorem (1978). Furthermore, it has the same conclusion as the Griffiths inequalities, but the hypotheses are different.
The inequality
Let be a finite distributive latticeDistributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
, and μ a positive function on it, that is assumed to satisfy the lattice condition, i.e.,
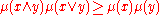
for all x, y in the lattice
.For any function
, its expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
with respect to μ is
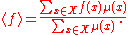
The FKG inequality then says that for any two monotonically increasing functions ƒ and g on
, the following positive correlation inequality holds:The same inequality (positive correlation) is true when both ƒ and g are decreasing.
If one is increasing and the other is decreasing, then they are negatively correlated:
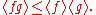
Similar statements hold more generally, when
is not necessarily finite, not even countable. In that case, μ has to be a finite measure, and the lattice condition has to be defined using cylinder events.For proofs, see the original or the Ahlswede-Daykin inequality (1978). Also, a rough sketch is given below, due to , using a Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
coupling
Coupling (probability)
In probability theory, coupling is a proof technique that allows one to compare two unrelated variables by "forcing" them to be related in some way.-Definition:...
argument.
Variations on terminology
The lattice condition for μ is also called multivariate total positivity, and sometimes the strong FKG condition.The property of μ that increasing functions are positively correlated is also called having positive associations, or the weak FKG condition.
Thus, the FKG theorem can be rephrased as "the strong FKG condition implies the weak FKG condition".
A special case: the Harris (Chebyshev's sum) inequality
If the lattice is totally ordered, then the lattice condition is satisfied trivially for any measure μ. For this case, the FKG inequality is Chebyshev's sum inequalityChebyshev's sum inequality
In mathematics, Chebyshev's sum inequality, named after Pafnuty Chebyshev, states that ifa_1 \geq a_2 \geq \cdots \geq a_nandb_1 \geq b_2 \geq \cdots \geq b_n,then...
: if the two increasing functions take on values
and , then (we may assume that measure μ is uniform)More generally, for any probability measure μ on
and increasing functions ƒ and g,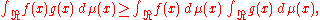which follows immediately from
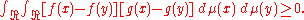
The lattice condition is trivially satisfied also when the lattice is the product of totally ordered lattices,
, and 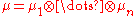is a product measure. Often all the factors (both the lattices and the measures) are identical, i.e., μ is the probability distribution of i.i.d. random variables.The FKG (Chebyshev's sum) inequality for the case of a product measure is known also as the Harris inequality after Harris , who used it in his study of percolation
Percolation theory
In mathematics, percolation theory describes the behavior of connected clusters in a random graph. The applications of percolation theory to materials science and other domains are discussed in the article percolation.-Introduction:...
in the plane. The proof given above can be found, e.g., in .
Simple examples
A typical example is the following. Color each hexagon of the infinite honeycomb lattice black with probability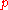 and white with probability 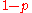, independently of each other. Let a, b, c, d be four hexagons, not necessarily distinct. Let and be the events that there is a black path from a to b, and a black path from c to d, respectively. Then the Harris inequality says that these events are positively correlated: 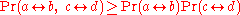. In other words, assuming the presence of one path can only increase the probability of the other.Similarly, if we randomly color the hexagons inside an
rhombus-shaped hex boardHex (board game)
Hex is a board game played on a hexagonal grid, theoretically of any size and several possible shapes, but traditionally as an 11x11 rhombus. Other popular dimensions are 13x13 and 19x19 as a result of the game's relationship to the older game of Go...
, then the events that there is black crossing from the left side of the board to the right side is positively correlated with having a black crossing from the top side to the bottom. On the other hand, having a left-to-right black crossing is negatively correlated with having a top-to-bottom white crossing, since the first is an increasing event (in the amount of blackness), while the second is decreasing. In fact, in any coloring of the hex board exactly one of these two events happen — this is why hex is a well-defined game.
In the Erdős-Rényi random graph, the existence of a Hamiltonian cycle is negatively correlated with the 3-colorability of the graph
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
, since the first is an increasing event, while the latter is decreasing.
Beyond product measures
In statistical mechanics, the usual source of measures that satisfy the lattice condition (and hence the FKG inequality) is the following:If
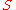is an ordered set (such as 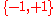), and is a finite or infinite graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, then the set
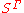of 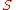-valued configurations is a poset that is a distributive lattice.Now, if
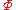is a submodular potentialGibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...
(i.e., a family of functions
one for each finite
, such that each 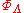is submodular), then one defines the corresponding HamiltonianGibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...
s as
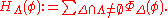
If μ is an extremal Gibbs measure
Gibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...
for this Hamiltonian on the set of configurations
, then it is easy to show that μ satisfies the lattice condition, see .A key example is the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
on a graph
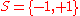. Let , called spins, and 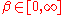. Take the following potential: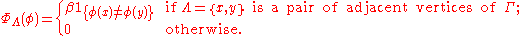Submodularity is easy to check; intuitively, taking the min or the max of two configurations tends to decrease the number of disagreeing spins. Then, depending on the graph
and the value of 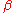, there could be one or more extremal Gibbs measures, see, e.g., and .A generalization: the Holley inequality
The Holley inequality, due to , states that the expectationsExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
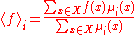
of a monotonically increasing function ƒ on a finite distributive lattice
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
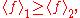
with respect to two positive functions μ1, μ2 on the lattice satisfy the conditionprovided the functions satisfy
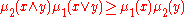
for all x, y in the lattice.
To get back the FKG inequality: If μ satisfies the lattice condition and ƒ and g are increasing functions on
, then μ1(x):=g(x)μ(x) and μ2(x):=μ(x) will satisfy the lattice-type condition of the Holley inequality. Then the Holley inequality says that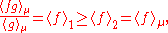which is just the FKG inequality.
Similarly to FKG, the Holley inequality also follows from the Ahlswede–Daykin inequality
Ahlswede–Daykin inequality
A fundamental tool in statistical mechanics and probabilistic combinatorics , the Ahlswede–Daykin inequality is a correlation-type inequality for four functions on a finite distributive lattice....
.
Weakening the lattice condition: monotonicity
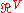Consider the usual case of being a product for some finite set . The lattice condition on μ is easily seen to imply the following monotonicity, which has the virtue that it is often easier to check than the lattice condition:Whenever one fixes a vertex
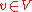and two configurations φ and ψ outside v such that 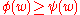for all 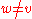, the μ-conditional distribution of φ(v) given stochastically dominatesStochastic ordering
In probability theory and statistics, a stochastic order quantifies the concept of one random variable being "bigger" than another. These are usually partial orders, so that one random variable A may be neither stochastically greater than, less than nor equal to another random variable B...
the μ-conditional distribution of ψ(v) given
.Now, if μ satisfies this monotonicity property, that is already enough for the FKG inequality (positive associations) to hold.
Here is a rough sketch of the proof, due to : starting from any initial configuration on
, one can run a simple Markov chainMarkov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
(the Metropolis algorithm) that uses independent Uniform[0,1] random variables to update the configuration in each step, such that the chain has a unique stationary measure, the given μ. The monotonicity of μ implies that the configuration at each step is a monotone function of independent variables, hence the product measure version of Harris implies that it has positive associations. Therefore, the limiting stationary measure μ also has this property.
The monotonicity property has a natural version for two measures, saying that μ1 conditionally pointwise dominates μ2. It is again easy to see that if μ1 and μ2 satisfy the lattice-type condition of the Holley inequality, then μ1 conditionally pointwise dominates μ2. On the other hand, a Markov chain coupling
Coupling (probability)
In probability theory, coupling is a proof technique that allows one to compare two unrelated variables by "forcing" them to be related in some way.-Definition:...
argument similar to the above, but now without invoking the Harris inequality, shows that conditional pointwise domination, in fact, implies stochastically domination
Stochastic ordering
In probability theory and statistics, a stochastic order quantifies the concept of one random variable being "bigger" than another. These are usually partial orders, so that one random variable A may be neither stochastically greater than, less than nor equal to another random variable B...
. Stochastic domination is equivalent to saying that
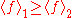for all increasing ƒ, thus we get a proof of the Holley inequality. (And thus also a proof of the FKG inequality, without using the Harris inequality.)See and for details.