
Ahlswede–Daykin inequality
Encyclopedia
A fundamental tool in statistical mechanics
and probabilistic combinatorics (especially random graph
s and the probabilistic method
), the Ahlswede–Daykin inequality
is a correlation
-type inequality for four functions on a finite distributive lattice
.
It states that if ƒi, i = 1, 2, 3, 4 are positive functions on a finite distributive lattice such that
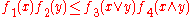
for all x, y in the lattice, then
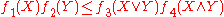
for all subsets X, Y of the lattice, where
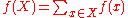
and
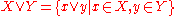
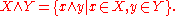
It implies the Holley inequality, which in turn implies the FKG inequality
. It also implies the Fishburn–Shepp inequality
.
For a proof, see the original article or .
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
and probabilistic combinatorics (especially random graph
Random graph
In mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
s and the probabilistic method
Probabilistic method
The probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
), the Ahlswede–Daykin inequality
is a correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
-type inequality for four functions on a finite distributive lattice
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
.
It states that if ƒi, i = 1, 2, 3, 4 are positive functions on a finite distributive lattice such that
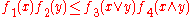
for all x, y in the lattice, then
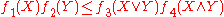
for all subsets X, Y of the lattice, where
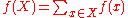
and
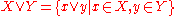
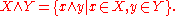
It implies the Holley inequality, which in turn implies the FKG inequality
FKG inequality
The FKG inequality is a correlation inequality, a fundamental tool in statistical mechanics and probabilistic combinatorics , due to...
. It also implies the Fishburn–Shepp inequality
Fishburn–Shepp inequality
In combinatorial mathematics, the Fishburn–Shepp inequality is an inequality for the number of extensions of partial orders to linear orders, found by and .It states that if x, y, and z are incomparable elements of a finite poset, then PIn combinatorial mathematics, the Fishburn–Shepp inequality...
.
For a proof, see the original article or .

