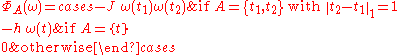Gibbs measure
Encyclopedia
In mathematics
, the Gibbs measure, named after Josiah Willard Gibbs
, is a probability measure
frequently seen in many problems of probability theory
and statistical mechanics
. It is the measure associated with the Boltzmann distribution
, and generalizes the notion of the canonical ensemble
. Importantly, when the energy function can be written as a sum of parts, the Gibbs measure has the Markov property
(a certain kind of statistical independence), thus leading to its widespread appearance in many problems outside of physics
, such as Hopfield networks, Markov network
s, and Markov logic network
s. In addition, the Gibbs measure is the unique measure that maximizes the entropy for a given expected energy; thus, the Gibbs measure underlies maximum entropy methods and the algorithms derived therefrom.
The measure gives the probability of the system X being in state x (equivalently, of the random variable
X having value x) as
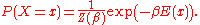
Here, is a function from the space of states to the real numbers; in physics applications,
is a function from the space of states to the real numbers; in physics applications, 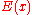 is interpreted as the energy of the configuration x. The parameter
is interpreted as the energy of the configuration x. The parameter 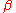 is a free parameter; in physics, it is the inverse temperature. The normalizing constant
is a free parameter; in physics, it is the inverse temperature. The normalizing constant
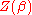 is the partition function
is the partition function
.
of the Gibbs measure can be seen in the Ising model
. Here, the probability of a given spin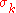 being in state s is, in principle, dependent on all other spins in the model; thus one writes
being in state s is, in principle, dependent on all other spins in the model; thus one writes
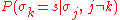
for this probability. However, the interactions in the Ising model are nearest-neighbor interactions, and thus, one actually has
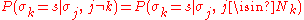
where is the set of nearest neighbors of site
is the set of nearest neighbors of site  . That is, the probability at site
. That is, the probability at site 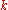 depends only on the nearest neighbors. This last equation is in the form of a Markov-type statistical independence. Measures with this property are sometimes called Markov random fields. More strongly, the converse is also true: any probability distribution having the Markov property can be represented with the Gibbs measure, given an appropriate energy function; this is the Hammersley–Clifford theorem
depends only on the nearest neighbors. This last equation is in the form of a Markov-type statistical independence. Measures with this property are sometimes called Markov random fields. More strongly, the converse is also true: any probability distribution having the Markov property can be represented with the Gibbs measure, given an appropriate energy function; this is the Hammersley–Clifford theorem
.
The definition of a Gibbs random field on a lattice
requires some terminology:
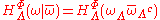 ,
,
 .
.
A probability measure
 on
on 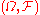 is a Gibbs measure for a
is a Gibbs measure for a 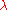 -admissible potential
-admissible potential 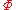 if it satisfies the Dobrushin-Lanford-Ruelle (DLR) equations
if it satisfies the Dobrushin-Lanford-Ruelle (DLR) equations
 ,
,
with nearest-neighbour interactions (coupling constant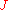 ) and a magnetic field (
) and a magnetic field (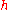 ), on
), on  :
:
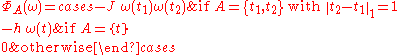
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Gibbs measure, named after Josiah Willard Gibbs
Josiah Willard Gibbs
Josiah Willard Gibbs was an American theoretical physicist, chemist, and mathematician. He devised much of the theoretical foundation for chemical thermodynamics as well as physical chemistry. As a mathematician, he invented vector analysis . Yale University awarded Gibbs the first American Ph.D...
, is a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
frequently seen in many problems of probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. It is the measure associated with the Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
, and generalizes the notion of the canonical ensemble
Canonical ensemble
The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...
. Importantly, when the energy function can be written as a sum of parts, the Gibbs measure has the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
(a certain kind of statistical independence), thus leading to its widespread appearance in many problems outside of physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, such as Hopfield networks, Markov network
Markov network
A Markov random field, Markov network or undirected graphical model is a set of variables having a Markov property described by an undirected graph. A Markov random field is similar to a Bayesian network in its representation of dependencies...
s, and Markov logic network
Markov logic network
A Markov logic network is a probabilistic logic which applies the ideas of a Markov network to first-order logic, enabling uncertain inference...
s. In addition, the Gibbs measure is the unique measure that maximizes the entropy for a given expected energy; thus, the Gibbs measure underlies maximum entropy methods and the algorithms derived therefrom.
The measure gives the probability of the system X being in state x (equivalently, of the random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X having value x) as
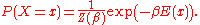
Here,
 is a function from the space of states to the real numbers; in physics applications,
is a function from the space of states to the real numbers; in physics applications, 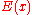 is interpreted as the energy of the configuration x. The parameter
is interpreted as the energy of the configuration x. The parameter 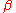 is a free parameter; in physics, it is the inverse temperature. The normalizing constant
is a free parameter; in physics, it is the inverse temperature. The normalizing constantNormalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
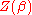 is the partition function
is the partition functionPartition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
.
Markov property
An example of the Markov propertyMarkov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
of the Gibbs measure can be seen in the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
. Here, the probability of a given spin
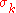 being in state s is, in principle, dependent on all other spins in the model; thus one writes
being in state s is, in principle, dependent on all other spins in the model; thus one writes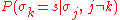
for this probability. However, the interactions in the Ising model are nearest-neighbor interactions, and thus, one actually has
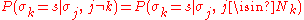
where
 is the set of nearest neighbors of site
is the set of nearest neighbors of site  . That is, the probability at site
. That is, the probability at site 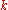 depends only on the nearest neighbors. This last equation is in the form of a Markov-type statistical independence. Measures with this property are sometimes called Markov random fields. More strongly, the converse is also true: any probability distribution having the Markov property can be represented with the Gibbs measure, given an appropriate energy function; this is the Hammersley–Clifford theorem
depends only on the nearest neighbors. This last equation is in the form of a Markov-type statistical independence. Measures with this property are sometimes called Markov random fields. More strongly, the converse is also true: any probability distribution having the Markov property can be represented with the Gibbs measure, given an appropriate energy function; this is the Hammersley–Clifford theoremHammersley–Clifford theorem
The Hammersley–Clifford theorem is a result in probability theory, mathematical statistics and statistical mechanics, that gives necessary and sufficient conditions under which a positive probability distribution can be represented as a Markov network...
.
Gibbs measure on lattices
What follows is a formal definition for the special case of a random field on a group lattice. The idea of a Gibbs measure is, however, much more general than this.The definition of a Gibbs random field on a lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
requires some terminology:
- The lattice: A countable set
 .
.
- The single-spin space: A probability spaceProbability spaceIn probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
 .
.
- The configuration spaceConfiguration space- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
: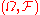 , where
, where  and
and 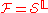 .
.
- Given a configuration
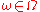 and a subset
and a subset  , the restriction of
, the restriction of  to
to 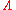 is
is 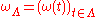 . If
. If  and
and 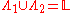 , then the configuration
, then the configuration 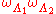 is the configuration whose restrictions to
is the configuration whose restrictions to 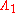 and
and  are
are 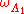 and
and 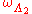 , respectively. These will be used to define cylinder setCylinder setIn mathematics, a cylinder set is the natural open set of a product topology. Cylinder sets are particularly useful in providing the base of the natural topology of the product of a countable number of copies of a set...
, respectively. These will be used to define cylinder setCylinder setIn mathematics, a cylinder set is the natural open set of a product topology. Cylinder sets are particularly useful in providing the base of the natural topology of the product of a countable number of copies of a set...
s, below.
- The set
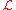 of all finite subsets of
of all finite subsets of  .
.
- For each subset
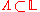 ,
, 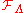 is the
is the  -algebra generated by the family of functions
-algebra generated by the family of functions 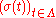 , where
, where 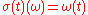 . This sigma-algebra is just the algebra of cylinder setCylinder setIn mathematics, a cylinder set is the natural open set of a product topology. Cylinder sets are particularly useful in providing the base of the natural topology of the product of a countable number of copies of a set...
. This sigma-algebra is just the algebra of cylinder setCylinder setIn mathematics, a cylinder set is the natural open set of a product topology. Cylinder sets are particularly useful in providing the base of the natural topology of the product of a countable number of copies of a set...
s on the lattice.
- The potentialPotential*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
: A family of functions
of functions  such that
such that
- For each
 ,
, 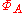 is
is 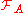 -measurable.
-measurable. - For all
 and
and  , the series
, the series 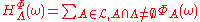 exists.
exists.
- For each
- The HamiltonianHamiltonianHamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...
in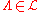 with boundary conditions
with boundary conditions  , for the potential
, for the potential 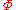 , is defined by
, is defined by
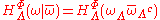 ,
,- where
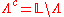 .
.
- The partition functionPartition function (statistical mechanics)Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
in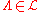 with boundary conditions
with boundary conditions  and inverse temperature
and inverse temperature  (for the potential
(for the potential 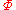 and
and 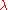 ) is defined by
) is defined by
 .
.- A potential
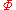 is
is 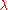 -admissible if
-admissible if 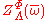 is finite for all
is finite for all 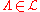 ,
,  and
and  .
.
A probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
 on
on 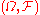 is a Gibbs measure for a
is a Gibbs measure for a 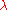 -admissible potential
-admissible potential 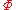 if it satisfies the Dobrushin-Lanford-Ruelle (DLR) equations
if it satisfies the Dobrushin-Lanford-Ruelle (DLR) equations ,
,- for all
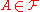 and
and 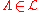 .
.
An example
To help understand the above definitions, here are the corresponding quantities in the important example of the Ising modelIsing model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
with nearest-neighbour interactions (coupling constant
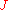 ) and a magnetic field (
) and a magnetic field (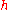 ), on
), on  :
:- The lattice is simply
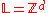 .
. - The single-spin space is
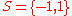 .
. - The potential is given by