
Euler integration
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computational science
Computational science
Computational science is the field of study concerned with constructing mathematical models and quantitative analysis techniques and using computers to analyze and solve scientific problems...
, the Euler method, named after Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, is a first-order numerical
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
procedure for solving ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s (ODEs) with a given initial value
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
. It is the most basic kind of explicit method
Explicit and implicit methods
Explicit and implicit methods are approaches used in numerical analysis for obtaining numerical solutions of time-dependent ordinary and partial differential equations, as is required in computer simulations of physical processes....
for numerical integration of ordinary differential equations
Numerical ordinary differential equations
Numerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
and is the simplest kind of Runge-Kutta method.
Informal geometrical description
Consider the problem of calculating the shape of an unknown curve which starts at a given point and satisfies a given differential equation. Here, a differential equation can be thought of as a formula by which the slopeSlope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of the tangent line to the curve can be computed at any point on the curve, once the position of that point has been calculated.
The idea is that while the curve is initially unknown, its starting point, which we denote by
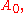 is known (see the picture on top right). Then, from the differential equation, the slope to the curve at
is known (see the picture on top right). Then, from the differential equation, the slope to the curve at  can be computed, and so, the tangent line.
can be computed, and so, the tangent line.Take a small step along that tangent line up to a point
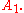 If we pretend that
If we pretend that 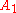 is still on the curve, the same reasoning as for the point
is still on the curve, the same reasoning as for the point 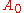 above can be used. After several steps, a polygonal curve
above can be used. After several steps, a polygonal curve 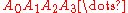 is computed. In general, this curve does not diverge too far from the original unknown curve, and the error between the two curves can be made small if the step size is small enough and the interval of computation is finite (although things are more complicated for stiff equation
is computed. In general, this curve does not diverge too far from the original unknown curve, and the error between the two curves can be made small if the step size is small enough and the interval of computation is finite (although things are more complicated for stiff equationStiff equation
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proved difficult to formulate a precise definition of stiffness, but the main idea is that...
s, as discussed below).
Derivation


by using the first two terms of the Taylor expansion of y, which represents the linear approximation around the point (t0,y(t0)) . One step of the Euler method from tn to tn+1 = tn + h is

The Euler method is explicit, i.e. the solution
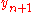 is an explicit function of
is an explicit function of  for
for  .
.While the Euler method integrates a first order ODE, any ODE of order N can be represented as a first-order ODE:
to treat the equation
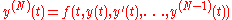 ,
,we introduce auxiliary variables
 and obtain
and obtainthe equivalent equation
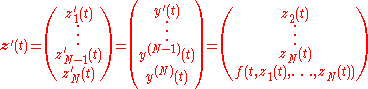
This is a first-order system in the variable
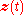 and can be handled by Euler's method or, in fact, any other scheme for first-order systems.
and can be handled by Euler's method or, in fact, any other scheme for first-order systems.Example
Given the differential equation and the initial point
and the initial point 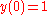 , we would like to use the Euler method to approximate
, we would like to use the Euler method to approximate  using step size
using step size  .
.The Euler method is

so first we must compute
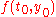 . This simple differential equation depends only on
. This simple differential equation depends only on 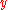 , so we need only worry about inputting the values for
, so we need only worry about inputting the values for 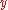 .
.
By doing the above step, we have found the slope of the line that is tangent to the solution curve at the point
 . Recall that the slope is defined as the change in
. Recall that the slope is defined as the change in  divided by the change in
divided by the change in  , or
, or 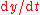 .
.The next step is to multiply the above value by the step size
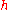 .
.
Since the step size is the change in
 , when we multiply the step size and the slope of the tangent, we get a change in
, when we multiply the step size and the slope of the tangent, we get a change in 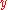 value. This value is then added to the initial
value. This value is then added to the initial 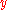 value to obtain the next value to be used for computations.
value to obtain the next value to be used for computations.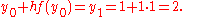
The above steps should be repeated to find
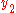 and
and  .
.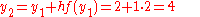
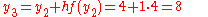
Due to the repetitive nature of this algorithm, it can be helpful to organize computations in a chart form, as seen below, to avoid making errors.
 | 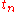 |  |  |  | 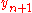 |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 | 2 |
| 2 | 1 | 2 | 1 | 2 | 4 |
| 4 | 2 | 4 | 1 | 4 | 8 |
Error
The magnitude of the errors arising from the Euler method can be demonstrated by comparison with a Taylor expansion of y. If we assume that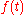 and
and 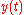 are known exactly at a time
are known exactly at a time  then the Euler method gives the approximate solution at time
then the Euler method gives the approximate solution at time  as:
as:
In comparison, the Taylor expansion in
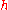 about
about  gives:
gives:
Since we know that
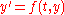 it follows that
it follows that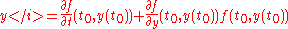
This, along with
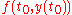 can be inserted into the Taylor expansion in
can be inserted into the Taylor expansion in  about
about  .
.
The error introduced by the Euler method is given by the difference between these equations:

For small
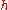 , the dominant error per step, or the local truncation error
, the dominant error per step, or the local truncation errorTruncation error (numerical integration)
Trunction errors in numerical integration are of two kinds:* local truncation errors – the error caused by one iteration, and* global truncation errors – the cumulative error cause by many iterations.- Definitions :...
, is proportional to
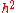 . To solve the problem over a given range of
. To solve the problem over a given range of  , the number of steps needed is proportional to
, the number of steps needed is proportional to 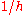 so it is to be expected that the total error at the end of the fixed time, or the global truncation error, will be proportional to
so it is to be expected that the total error at the end of the fixed time, or the global truncation error, will be proportional to 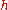 (error per step times number of steps). Because the global truncation error is proportional to
(error per step times number of steps). Because the global truncation error is proportional to  , the Euler method is said to be first order. This makes the Euler method less accurate (for small
, the Euler method is said to be first order. This makes the Euler method less accurate (for small 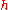 ) than other higher-order techniques such as Runge-Kutta methods and linear multistep methods.
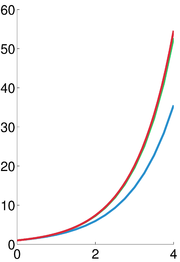
) than other higher-order techniques such as Runge-Kutta methods and linear multistep methods.As stated in the introduction, decreasing the step size can help to make the approximation more accurate and decrease the error between the two curves. The error to three decimal places for the example in the above section (with step size
 )is the following:
)is the following: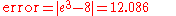
When the step size is changed to
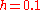 our
our  value becomes
value becomes  . The error, then, for step size
. The error, then, for step size  is the following:
is the following: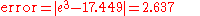
Although the error has decreased, our approximation is still not particularly accurate. In addition, since the step size decreased with no change in the interval, the number of iterations has increased to thirty. While possible, it is no longer reasonable to do these computations by hand.
Error bound
As with other methods, there is a way for us to determine an error bound for a particular problem. The error bound on the global error is given by: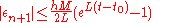
where
 is the step size,
is the step size,  is the upper bound on the second derivative of
is the upper bound on the second derivative of  on the given interval (which must be estimated), and
on the given interval (which must be estimated), and  is the Lipschitz constant
is the Lipschitz constantLipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
.
If the error bound is computed, it can be seen, once again, that if small error is desired, the step size
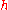 must be very small.
must be very small.For instance, let us calculate the step size required for global truncation error to be
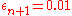 , assuming a maximum value for the second derivative of
, assuming a maximum value for the second derivative of  , a Lipschitz constant of
, a Lipschitz constant of  , and
, and  from zero to four. Using the equation given, we obtain the following:
from zero to four. Using the equation given, we obtain the following:


which means that h must be smaller than the above to get the desired error or less, and 4/h, or about 1072 iterations will need to be completed to do so. The large number of steps, and thus high computation cost, supports the use of alternative, higher-order methods such as Runge–Kutta methods or linear multistep methods.
Numerical stability
The Euler method can also be numerically unstableNumerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
, especially for stiff equation
Stiff equation
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proved difficult to formulate a precise definition of stiffness, but the main idea is that...
s. This limitation—along with its slow convergence of error with h—means that the Euler method is not often used, except as a simple example of numerical integration. The instability can be avoided by using the Euler–Cromer algorithm.
See also
- Numerical integration of ordinary differential equationsNumerical ordinary differential equationsNumerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
- For numerical methods for calculating definite integrals, see Numerical integrationNumerical integrationIn numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
- Gradient descentGradient descentGradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
similarly uses finite steps, here to find minima of functions

