Easton's theorem
Encyclopedia
In set theory
, Easton's theorem is a result on the possible cardinal number
s of powersets. (extending a result of Robert M. Solovay
) showed via forcing
that
and, for
, that
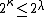
are the only constraints on permissible values for 2κ when κ is a regular cardinal
.
and whose range consists of ordinals such that
then there is a model of ZFC such that
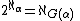
for each
in the domain of G.
The proof of Easton's theorem uses forcing
with a proper class of forcing conditions.
All conditions in the theorem are necessary. Condition 1 is a well known property of cardinality, while condition 2 follows from König's theorem
.
The program of PCF theory
gives results on the possible values of
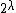for singular cardinals 
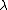. PCF theory shows that the values of the continuum function on singular cardinals are strongly influenced by the values on smaller cardinals, whereas Easton's theorem shows that the values of the continuum function on regular cardinal
s are only weakly influenced by the values on smaller cardinals.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, Easton's theorem is a result on the possible cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s of powersets. (extending a result of Robert M. Solovay
Robert M. Solovay
Robert Martin Solovay is an American mathematician specializing in set theory.Solovay earned his Ph.D. from the University of Chicago in 1964 under the direction of Saunders Mac Lane, with a dissertation on A Functorial Form of the Differentiable Riemann–Roch theorem...
) showed via forcing
Forcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
that
and, for
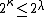
, thatare the only constraints on permissible values for 2κ when κ is a regular cardinal
Regular cardinal
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
.
Statement of the theorem
Easton's theorem states that if G is a class function whose domain consists of ordinalsOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
and whose range consists of ordinals such that
- G is non-decreasing,
- the cofinalityCofinalityIn mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
of
is greater than 
for each α in the domain of G, and -
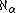is regular for each α in the domain of G,
then there is a model of ZFC such that
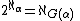
for each
in the domain of G.The proof of Easton's theorem uses forcing
Forcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
with a proper class of forcing conditions.
All conditions in the theorem are necessary. Condition 1 is a well known property of cardinality, while condition 2 follows from König's theorem
König's theorem (set theory)
In set theory, König's theorem colloquially states that if the axiom of choice holds, I is a set, mi and ni are cardinal numbers for every i in I, and m_i In set theory, König's theorem In set theory, König's theorem (named after the Hungarian mathematician Gyula Kőnig, who published under the...
.
No extension to singular cardinals
proved that a singular cardinal of uncountable cofinality cannot be the smallest cardinal for which the generalized continuum hypothesis fails. This shows that Easton's theorem cannot be extended to the class of all cardinals.The program of PCF theory
PCF theory
PCF theory is the name of a mathematical theory, introduced by Saharon , that deals with the cofinality of the ultraproducts of ordered sets. It gives strong upper bounds on the cardinalities of power sets of singular cardinals, and has many more applications as well...
gives results on the possible values of
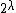for singular cardinals 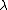. PCF theory shows that the values of the continuum function on singular cardinals are strongly influenced by the values on smaller cardinals, whereas Easton's theorem shows that the values of the continuum function on regular cardinalRegular cardinal
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
s are only weakly influenced by the values on smaller cardinals.
See also
- Singular cardinal hypothesisSingular cardinal hypothesisIn set theory, the singular cardinals hypothesis arose from the question of whether the least cardinal number for which the generalized continuum hypothesis might fail could be a singular cardinal....
- König's theorem (set theory)König's theorem (set theory)In set theory, König's theorem colloquially states that if the axiom of choice holds, I is a set, mi and ni are cardinal numbers for every i in I, and m_i In set theory, König's theorem In set theory, König's theorem (named after the Hungarian mathematician Gyula Kőnig, who published under the...
- CofinalityCofinalityIn mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
- Aleph numberAleph numberIn set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
- Beth numberBeth numberIn mathematics, the infinite cardinal numbers are represented by the Hebrew letter \aleph indexed with a subscript that runs over the ordinal numbers...
- Continuum hypothesisContinuum hypothesisIn mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
- Continuum functionContinuum functionThe continuum function is \kappa\mapsto 2^\kappa, i.e. raising 2 to the power of κ using cardinal exponentiation. Given a cardinal number, it is the cardinality of the power set of a set of the given cardinality.-See also:*Continuum hypothesis...