Continuum function
Encyclopedia
The continuum function is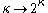 
, i.e. raising 2 to the power of κ using cardinal exponentiation. Given a cardinal number
, it is the cardinality of the power set of a set of the given cardinality.
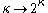, i.e. raising 2 to the power of κ using cardinal exponentiation. Given a cardinal numberCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
, it is the cardinality of the power set of a set of the given cardinality.
See also
- Continuum hypothesisContinuum hypothesisIn mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
- Cardinality of the continuumCardinality of the continuumIn set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
- Beth numberBeth numberIn mathematics, the infinite cardinal numbers are represented by the Hebrew letter \aleph indexed with a subscript that runs over the ordinal numbers...
- Gimel function