
EXPSPACE
Encyclopedia
In complexity theory
, EXPSPACE is the set of all decision problem
s solvable by a deterministic Turing machine
in O
(2p(n)) space, where p(n) is a polynomial function of n. (Some authors restrict p(n) to be a linear function
, but most authors instead call the resulting class ESPACE
.) If we use a nondeterministic machine instead, we get the class NEXPSPACE, which is equal to EXPSPACE by Savitch's theorem
.
In terms of DSPACE
and NSPACE
,
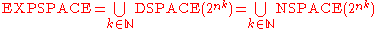
A decision problem is EXPSPACE-complete if it is in EXPSPACE, and every problem in EXPSPACE has a polynomial-time many-one reduction to it. In other words, there is a polynomial-time algorithm
that transforms instances of one to instances of the other with the same answer. EXPSPACE-complete problems might be thought of as the hardest problems in EXPSPACE.
EXPSPACE is a strict superset of PSPACE
, NP
, and P
and is believed to be a strict superset of EXPTIME
.
An example of an EXPSPACE-complete problem is the problem of recognizing whether two regular expression
s represent different languages, where the expressions are limited to four operators: union, concatenation
, the Kleene star
(zero or more copies of an expression), and squaring (two copies of an expression).
If the Kleene star is left out, then that problem becomes NEXPTIME
-complete, which is like EXPTIME-complete, except it is defined in terms of non-deterministic Turing machine
s rather than deterministic.
It has also been shown by L. Berman in 1980 that the problem of verifying/falsifying any first-order
statement about real number
s that involves only addition
and comparison (but no multiplication
) is in EXPSPACE.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, EXPSPACE is the set of all decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
s solvable by a deterministic Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
in O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(2p(n)) space, where p(n) is a polynomial function of n. (Some authors restrict p(n) to be a linear function
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
, but most authors instead call the resulting class ESPACE
ESPACE
For the car, see Renault EspaceIn computational complexity theory, the complexity class ESPACE is the set of decision problems that can be solved by a deterministic Turing machine in space 2O.See also EXPSPACE....
.) If we use a nondeterministic machine instead, we get the class NEXPSPACE, which is equal to EXPSPACE by Savitch's theorem
Savitch's theorem
In computational complexity theory, Savitch's theorem, proved by Walter Savitch in 1970, states that for any function ƒ ≥ log,...
.
In terms of DSPACE
DSPACE
In computational complexity theory, DSPACE or SPACE is the computational resource describing the resource of memory space for a deterministic Turing machine. It represents the total amount of memory space that a "normal" physical computer would need to solve a given computational problem with a...
and NSPACE
NSPACE
In computational complexity theory, the complexity class NSPACE is the set of decision problems that can be solved by a non-deterministic Turing machine using space O, and unlimited time. It is the non-deterministic counterpart of DSPACE.Several important complexity classes can be defined in terms...
,
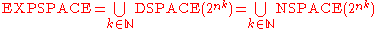
A decision problem is EXPSPACE-complete if it is in EXPSPACE, and every problem in EXPSPACE has a polynomial-time many-one reduction to it. In other words, there is a polynomial-time algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that transforms instances of one to instances of the other with the same answer. EXPSPACE-complete problems might be thought of as the hardest problems in EXPSPACE.
EXPSPACE is a strict superset of PSPACE
PSPACE
In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
, NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
, and P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
and is believed to be a strict superset of EXPTIME
EXPTIME
In computational complexity theory, the complexity class EXPTIME is the set of all decision problems solvable by a deterministic Turing machine in O time, where p is a polynomial function of n....
.
An example of an EXPSPACE-complete problem is the problem of recognizing whether two regular expression
Regular expression
In computing, a regular expression provides a concise and flexible means for "matching" strings of text, such as particular characters, words, or patterns of characters. Abbreviations for "regular expression" include "regex" and "regexp"...
s represent different languages, where the expressions are limited to four operators: union, concatenation
Concatenation
In computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
, the Kleene star
Kleene star
In mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
(zero or more copies of an expression), and squaring (two copies of an expression).
If the Kleene star is left out, then that problem becomes NEXPTIME
NEXPTIME
In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O for some polynomial p, and unlimited space....
-complete, which is like EXPTIME-complete, except it is defined in terms of non-deterministic Turing machine
Non-deterministic Turing machine
In theoretical computer science, a Turing machine is a theoretical machine that is used in thought experiments to examine the abilities and limitations of computers....
s rather than deterministic.
It has also been shown by L. Berman in 1980 that the problem of verifying/falsifying any first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
statement about real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s that involves only addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and comparison (but no multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
) is in EXPSPACE.

