.gif)
Dunce hat (topology)
Encyclopedia
For the item of clothing designed to be humiliating, now rarely used, see dunce cap
.
 In topology
In topology
, the dunce hat is a compact
topological space
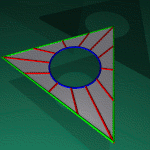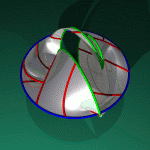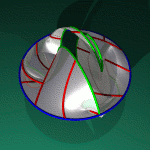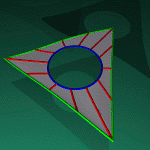
formed by taking a solid triangle
and gluing
all three sides together, with the orientation of one side reversed. Simply gluing two sides oriented in the same direction would yield a cone much like the layman's dunce cap, but the gluing of the third side results in identifying the base of the cap with a line joining the base to the point.
The dunce hat is contractible
, but not collapsible. Contractibility can be easily seen by noting that the dunce hat embeds in the 3-ball and the 3-ball deformation retracts onto the dunce hat. Alternatively, note that the dunce hat is the CW-complex obtained by gluing the boundary of a 2-cell onto the circle. The gluing map is homotopic to the identity map on the circle and so the complex is homotopy equivalent to the disc. By contrast, it is not collapsible because it does not have a free face.
The name is due to E. C. Zeeman, who observed that any contractible 2-complex (such as the dunce hat) after taking the Cartesian product with the closed unit interval seemed to be collapsible. This observation became known as the Zeeman conjecture and was shown by Zeeman to imply the Poincaré conjecture
.
Dunce cap
A dunce cap, also variously known as a dunce hat, dunce's cap, or dunce's hat, is a pointed hat. In popular culture, it is typically made of paper and often marked with a D or the word "dunce", and given to schoolchildren to wear as punishment by public humiliation for misbehavior and, as the name...
.

Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the dunce hat is a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
formed by taking a solid triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
and gluing
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
all three sides together, with the orientation of one side reversed. Simply gluing two sides oriented in the same direction would yield a cone much like the layman's dunce cap, but the gluing of the third side results in identifying the base of the cap with a line joining the base to the point.
The dunce hat is contractible
Contractible space
In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
, but not collapsible. Contractibility can be easily seen by noting that the dunce hat embeds in the 3-ball and the 3-ball deformation retracts onto the dunce hat. Alternatively, note that the dunce hat is the CW-complex obtained by gluing the boundary of a 2-cell onto the circle. The gluing map is homotopic to the identity map on the circle and so the complex is homotopy equivalent to the disc. By contrast, it is not collapsible because it does not have a free face.
The name is due to E. C. Zeeman, who observed that any contractible 2-complex (such as the dunce hat) after taking the Cartesian product with the closed unit interval seemed to be collapsible. This observation became known as the Zeeman conjecture and was shown by Zeeman to imply the Poincaré conjecture
Poincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
.


