Distance of closest approach of ellipses and ellipsoids
Encyclopedia
The distance of closest approach of two objects is the distance between their centers when they are externally tangent. The objects may be geometric shapes or physical particles with well defined boundaries. The distance of closest approach is sometimes referred to as the contact distance.
For the simplest objects, spheres, the distance of closest approach is simply the sum of their radii. For non-spherical objects, the distance of closest approach is a function of the orientation of the objects, and its calculation can be difficult. The maximum packing density of hard particles, an important problem of ongoing interest, depends on their distance of closest approach.
The interactions of particles typically depend on their separation, and the distance of closest approach plays an important role in determining the behavior of condensed matter systems.
The excluded volume
of particles (the volume excluded to the centers of other particles due to the presence of one) is a key parameter in such descriptions,; the distance of closest approach is required to calculate the excluded volume. The excluded volume for identical spheres is just four times the volume of one sphere
. For other anisotropic objects, the excluded volume depends on orientation, and its calculation can be surprising difficult. The simplest shapes after spheres are ellipses and ellipsoids; these have received considerable attention, yet their excluded volume is not known. Vieillard Baron was able to provide an overlap criterion for two ellipses. His results were useful for computer simulations of hard particle systems and for packing problem
s using Monte Carlo
simulations.
The one anisotropic shape whose excluded volume can be expressed analytically is the spherocylinder; the solution of this problem is a classic work by Onsager. The problem was tackled by considering the distance between two line segments, which are the center lines of the capped cylinders. Results for other shapes are not readily available.
The orientation dependence of the distance of closest approach has surprising consequences. Systems of hard particles, whose interactions are only entropic, can become ordered. Hard spherocylinders form not only orientationally ordered nematic, but also positionally ordered smectic phases. Here, the system gives up some (orientational and even positional) disorder to gain disorder and entropy
elsewhere.
using Monte Carlo
simulations. Although overlap criteria have been developed, analytic solutions for the distance of closest approach and the location of the point of contact have only recently become available. The details of the calculations are provided in Ref. The Fortran 90 subroutine is provided in Ref.
Input:
Output:
and orientation
, whose centers are on a line with given direction. We wish to determine the distance between centers when the ellipsoids are in point contact externally. This distance of closest approach is a function of the shapes of the ellipsoids and their orientation. There is no analytic solution for this problem, since solving for the distance requires the solution of a sixth order polynomial equation. Here an algorithm
is developed to determine this distance, based on the analytic results for the distance of closest approach of ellipses in 2D, which can be implemented numerically. Details are given in publications. Subroutines are provided in two formats: Fortran90 and C.
For the simplest objects, spheres, the distance of closest approach is simply the sum of their radii. For non-spherical objects, the distance of closest approach is a function of the orientation of the objects, and its calculation can be difficult. The maximum packing density of hard particles, an important problem of ongoing interest, depends on their distance of closest approach.
The interactions of particles typically depend on their separation, and the distance of closest approach plays an important role in determining the behavior of condensed matter systems.
The excluded volume
Excluded volume
The concept of excluded volume was introduced by Werner Kuhn in 1934 and applied to polymer molecules shortly thereafter by Paul Flory.- In liquid state theory :...
of particles (the volume excluded to the centers of other particles due to the presence of one) is a key parameter in such descriptions,; the distance of closest approach is required to calculate the excluded volume. The excluded volume for identical spheres is just four times the volume of one sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
. For other anisotropic objects, the excluded volume depends on orientation, and its calculation can be surprising difficult. The simplest shapes after spheres are ellipses and ellipsoids; these have received considerable attention, yet their excluded volume is not known. Vieillard Baron was able to provide an overlap criterion for two ellipses. His results were useful for computer simulations of hard particle systems and for packing problem
Packing problem
Packing problems are a class of optimization problems in mathematics which involve attempting to pack objects together , as densely as possible. Many of these problems can be related to real life packaging, storage and transportation issues...
s using Monte Carlo
Monte Carlo
Monte Carlo is an administrative area of the Principality of Monaco....
simulations.
The one anisotropic shape whose excluded volume can be expressed analytically is the spherocylinder; the solution of this problem is a classic work by Onsager. The problem was tackled by considering the distance between two line segments, which are the center lines of the capped cylinders. Results for other shapes are not readily available.
The orientation dependence of the distance of closest approach has surprising consequences. Systems of hard particles, whose interactions are only entropic, can become ordered. Hard spherocylinders form not only orientationally ordered nematic, but also positionally ordered smectic phases. Here, the system gives up some (orientational and even positional) disorder to gain disorder and entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
elsewhere.
Distance of closest approach of two ellipses
Vieillard Baron first investigated this problem, although he did not obtain a result for the distance of closest approach, he derived the overlap criterion for two ellipses. His results were useful for the study of the phase behavior of hard particles and for the packing problemPacking problem
Packing problems are a class of optimization problems in mathematics which involve attempting to pack objects together , as densely as possible. Many of these problems can be related to real life packaging, storage and transportation issues...
using Monte Carlo
Monte Carlo
Monte Carlo is an administrative area of the Principality of Monaco....
simulations. Although overlap criteria have been developed, analytic solutions for the distance of closest approach and the location of the point of contact have only recently become available. The details of the calculations are provided in Ref. The Fortran 90 subroutine is provided in Ref.
The method
The procedure consists of three steps:- Transformation of the two tangentTangentIn geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s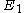
and 
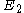, whose centers are joined by the vector 
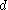, into a circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
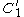and an ellipse 
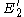, whose centers are joined by the vector 
. The circle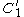 
and the ellipse 
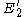remain tangent after the transformation. - Determination of the distance
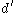of closest approach of 
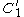and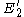 
analytically. It requires the appropriate solution of a quartic equation. The normal 
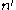is calculated. - Determination of the distance
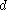of closest approach and the location of the point of contact of 
and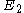 
by the inverse transformations of the vectors 
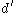and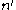 
.
Input:
- lengths of the semiaxes
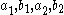, - unit vectors
,
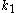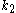along major axesAxesAxes may refer to:* Axes, woodworking hand tools* The plural of axis* Axes , a 2005 rock album by the British band Electrelane* X and Y axes, or X, Y, and Z axes, perpendicular lines used in the Cartesian coordinate system...
of both ellipses, and - unit vector
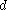joining the centers of the two ellipses.
Output:
- distance
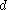between the centers when the ellipses 
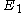and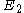 
are externally tangentTangentIn geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
, and - location of point of contact in terms of
,
.
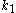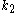Distance of closest approach of two ellipsoids
Consider two ellipsoids, each with a given shapeShape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
and orientation
Orientation (geometry)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
, whose centers are on a line with given direction. We wish to determine the distance between centers when the ellipsoids are in point contact externally. This distance of closest approach is a function of the shapes of the ellipsoids and their orientation. There is no analytic solution for this problem, since solving for the distance requires the solution of a sixth order polynomial equation. Here an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
is developed to determine this distance, based on the analytic results for the distance of closest approach of ellipses in 2D, which can be implemented numerically. Details are given in publications. Subroutines are provided in two formats: Fortran90 and C.
Method
The algorithm consists of three steps.- Constructing a plane containing the line joining the centers of the two ellipsoids, and finding the equations of the ellipses formed by the intersectionIntersectionIntersection has various meanings in different contexts:*In mathematics and geometry**Intersection , the set of elements common to some collection of sets.**Line-line intersection**Line-plane intersection**Line–sphere intersection...
of this plane and the ellipsoids. - Determining the distance of closest approach of the ellipses; that is the distance between the centers of the ellipses when they are in point contact externally.
- Rotating the plane until the distance of closest approach of the ellipses is a maximum. The distance of closest approach of the ellipsoids is this maximum distance.