Disjoint-set data structure
Encyclopedia
In computing
, a disjoint-set data structure is a data structure
that keeps track of a set of elements partitioned
into a number of disjoint (nonoverlapping) subsets. A union-find algorithm is an algorithm that performs two useful operations on such a data structure:
Because it supports these two operations, a disjoint-set data structure is sometimes called a union-find data structure or merge-find set. The other important operation, MakeSet, which makes a set containing only a given element (a singleton), is generally trivial. With these three operations, many practical partitioning problems can be solved (see the Applications section).
In order to define these operations more precisely, some way of representing the sets is needed. One common approach is to select a fixed element of each set, called its representative, to represent the set as a whole. Then, Find(x) returns the representative of the set that x belongs to, and Union takes two set representatives as its arguments.
for each set. The element at the head of each list is chosen as its representative.
MakeSet creates a list of one element. Union appends the two lists, a constant-time operation. The drawback of this implementation is that Find requires Ω(n) or linear time to traverse the list backwards from a given element to the head of the list.
This can be avoided by including in each linked list node a pointer to the head of the list; then Find takes constant time, since this pointer refers directly to the set representative. However, Union now has to update each element of the list being appended to make it point to the head of the new combined list, requiring Ω(n) time.
When the length of each list is tracked, the required time can be improved by always appending the smaller list to the longer. Using this weighted-union heuristic, a sequence of m MakeSet, Union, and Find operations on n elements requires O(m + nlog n) time. For asymptotically faster operations, a different data structure is needed.
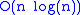above.
Suppose you have a collection of lists, each node of a list contains an object, the name of the list to which it belongs, and the number of elements in that list. Also assume that the sum of the number of elements in all lists is
(i.e. there are 
elements overall). We wish to be able to merge any two of these lists, and update all of their nodes so that they still contain the name of the list to which they belong. The rule for merging the lists 
and 
is that if 
is larger than 
then merge the elements of 
into 
and update the elements that used to belong to 
, and vice versa.
Choose an arbitrary element of list
, say 
. We wish to count how many times in the worst case will 
need to have the name of the list to which it belongs updated. The element 
will only have its name updated when the list it belongs to is merged with another list of the same size or of greater size. Each time that happens, the size of the list to which 
belongs at least doubles. So finally, the question is "how many times can a number double before it is the size of 
?" (then the list containing 
will contain all 
elements). The answer is exactly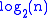 
. So for any given element of any given list in the structure described, it will need to be updated 
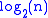times in the worst case. Therefore updating a list of 
elements stored in this way takes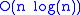 
time in the worst case. A find operation can be done in 
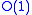for this structure because each node contains the name of the list to which it belongs.
A similar argument holds for merging the trees in the data structures discussed below, additionally it helps explain the time analysis of some operations in the binomial heap
and Fibonacci heap
data structures.
to its parent node (see spaghetti stack
). They were first described by Bernard A. Galler and Michael J. Fischer
in 1964, although their precise analysis took years.
In a disjoint-set forest, the representative of each set is the root of that set's tree. Find follows parent nodes until it reaches the root. Union combines two trees into one by attaching the root of one to the root of the other. One way of implementing these might be:
function MakeSet(x)
x.parent := x
function Find(x)
if x.parent x
return x
else
return Find(x.parent)
function Union(x, y)
xRoot := Find(x)
yRoot := Find(y)
xRoot.parent := yRoot
In this naive form, this approach is no better than the linked-list approach, because the tree it creates can be highly unbalanced; however, it can be enhanced in two ways.
The first way, called union by rank, is to always attach the smaller tree to the root of the larger tree, rather than vice versa. Since it is the depth of the tree that affects the running time, the tree with smaller depth gets added under the root of the deeper tree, which only increases the depth if the depths were equal. In the context of this algorithm, the term rank is used instead of depth since it stops being equal to the depth if path compression (described below) is also used. One-element trees are defined to have a rank of zero, and whenever two trees of the same rank r are united, the rank of the result is r+1. Just applying this technique alone yields an amortized
running-time of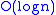
per MakeSet, Union, or Find operation. Pseudocode for the improved
function MakeSet(x)
x.parent := x
x.rank := 0
function Union(x, y)
xRoot := Find(x)
yRoot := Find(y)
if xRoot yRoot
return
// x and y are not already in same set. Merge them.
if xRoot.rank < yRoot.rank
xRoot.parent := yRoot
else if xRoot.rank > yRoot.rank
yRoot.parent := xRoot
else
yRoot.parent := xRoot
xRoot.rank := xRoot.rank + 1
The second improvement, called path compression, is a way of flattening the structure of the tree whenever Find is used on it. The idea is that each node visited on the way to a root node may as well be attached directly to the root node; they all share the same representative. To effect this, as
function Find(x)
if x.parent x
return x
else
x.parent := Find(x.parent)
return x.parent
These two techniques complement each other; applied together, the amortized
time per operation is only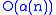
, where 
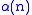is the inverse of the function 
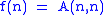, and 
is the extremely quickly-growing Ackermann function
. Since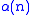
is the inverse of this function, 
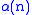is less than 5 for all remotely practical values of 
. Thus, the amortized running time per operation is effectively a small constant.
In fact, this is asymptotically optimal
: Fredman
and Saks showed in 1989 that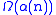
words must be accessed by any disjoint-set data structure per operation on average.
Applications
Disjoint-set data structures model the partitioning of a set
, for example to keep track of the connected components
of an undirected graph. This model can then be used to determine whether two vertices belong to the same component, or whether adding an edge between them would result in a cycle. The Union-Find algorithm is used in high-performance implementations of Unification.
This data structure is used by the Boost Graph Library to implement its Incremental Connected Components functionality. It is also used for implementing Kruskal's algorithm
to find the minimum spanning tree
of a graph.
Note that the implementation as disjoint-set forests doesn't allow deletion of edges—even without path compression or the rank heuristic.
History
While the ideas used in disjoint-set forests have long been familiar, Robert Tarjan
was the first to prove the upper bound (and a restricted version of the lower bound) in terms of the inverse Ackermann function
, in 1975.
Until this time the best bound on the time per operation, proven by Hopcroft
and Ullman
,
was O(log* n), the iterated logarithm
of n, another slowly-growing function (but not quite as slow as the inverse Ackermann function).
Tarjan and Van Leeuwen
also developed one-pass Find algorithms that are more efficient in practice while retaining the same worst-case complexity.
In 2007, Sylvain Conchon and Jean-Christophe Filliâtre developed a persistent
version of the disjoint-set forest data structure, allowing previous versions of the structure to be efficiently retained, and formalized its correctness using the proof assistant Coq
.
See also
External links
Computing
Computing is usually defined as the activity of using and improving computer hardware and software. It is the computer-specific part of information technology...
, a disjoint-set data structure is a data structure
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
that keeps track of a set of elements partitioned
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
into a number of disjoint (nonoverlapping) subsets. A union-find algorithm is an algorithm that performs two useful operations on such a data structure:
- Find: Determine which set a particular element is in. Also useful for determining if two elements are in the same set.
- Union: Combine or merge two sets into a single set.
Because it supports these two operations, a disjoint-set data structure is sometimes called a union-find data structure or merge-find set. The other important operation, MakeSet, which makes a set containing only a given element (a singleton), is generally trivial. With these three operations, many practical partitioning problems can be solved (see the Applications section).
In order to define these operations more precisely, some way of representing the sets is needed. One common approach is to select a fixed element of each set, called its representative, to represent the set as a whole. Then, Find(x) returns the representative of the set that x belongs to, and Union takes two set representatives as its arguments.
Disjoint-set linked lists
A simple approach to creating a disjoint-set data structure is to create a linked listLinked list
In computer science, a linked list is a data structure consisting of a group of nodes which together represent a sequence. Under the simplest form, each node is composed of a datum and a reference to the next node in the sequence; more complex variants add additional links...
for each set. The element at the head of each list is chosen as its representative.
MakeSet creates a list of one element. Union appends the two lists, a constant-time operation. The drawback of this implementation is that Find requires Ω(n) or linear time to traverse the list backwards from a given element to the head of the list.
This can be avoided by including in each linked list node a pointer to the head of the list; then Find takes constant time, since this pointer refers directly to the set representative. However, Union now has to update each element of the list being appended to make it point to the head of the new combined list, requiring Ω(n) time.
When the length of each list is tracked, the required time can be improved by always appending the smaller list to the longer. Using this weighted-union heuristic, a sequence of m MakeSet, Union, and Find operations on n elements requires O(m + nlog n) time. For asymptotically faster operations, a different data structure is needed.
Analysis of the naïve approach
We now explain the bound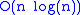 above.Suppose you have a collection of lists, each node of a list contains an object, the name of the list to which it belongs, and the number of elements in that list. Also assume that the sum of the number of elements in all lists is
(i.e. there are elements overall). We wish to be able to merge any two of these lists, and update all of their nodes so that they still contain the name of the list to which they belong. The rule for merging the lists and is that if is larger than then merge the elements of into and update the elements that used to belong to , and vice versa.Choose an arbitrary element of list
, say . We wish to count how many times in the worst case will need to have the name of the list to which it belongs updated. The element will only have its name updated when the list it belongs to is merged with another list of the same size or of greater size. Each time that happens, the size of the list to which belongs at least doubles. So finally, the question is "how many times can a number double before it is the size of ?" (then the list containing will contain all elements). The answer is exactly 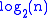. So for any given element of any given list in the structure described, it will need to be updated 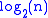times in the worst case. Therefore updating a list of elements stored in this way takes 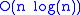time in the worst case. A find operation can be done in 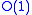for this structure because each node contains the name of the list to which it belongs.A similar argument holds for merging the trees in the data structures discussed below, additionally it helps explain the time analysis of some operations in the binomial heap
Binomial heap
In computer science, a binomial heap is a heap similar to a binary heap but also supports quickly merging two heaps. This is achieved by using a special tree structure...
and Fibonacci heap
Fibonacci heap
In computer science, a Fibonacci heap is a heap data structure consisting of a collection of trees. It has a better amortized running time than a binomial heap. Fibonacci heaps were developed by Michael L. Fredman and Robert E. Tarjan in 1984 and first published in a scientific journal in 1987...
data structures.
Disjoint-set forests
Disjoint-set forests are a data structure where each set is represented by a tree data structure, in which each node holds a referenceReference
Reference is derived from Middle English referren, from Middle French rèférer, from Latin referre, "to carry back", formed from the prefix re- and ferre, "to bear"...
to its parent node (see spaghetti stack
Spaghetti stack
A spaghetti stack in computer science is an N-ary tree data structure in which child nodes have pointers to the parent nodes . When a list of nodes is traversed from a leaf node to the root node by chasing these parent pointers, the structure looks like a linked list stack...
). They were first described by Bernard A. Galler and Michael J. Fischer
Michael J. Fischer
Michael John Fischer is a computer scientist who works in the fields of distributed computing, parallel computing, cryptography, algorithms and data structures, and computational complexity.-Career:...
in 1964, although their precise analysis took years.
In a disjoint-set forest, the representative of each set is the root of that set's tree. Find follows parent nodes until it reaches the root. Union combines two trees into one by attaching the root of one to the root of the other. One way of implementing these might be:
function MakeSet(x)
x.parent := x
function Find(x)
if x.parent x
return x
else
return Find(x.parent)
function Union(x, y)
xRoot := Find(x)
yRoot := Find(y)
xRoot.parent := yRoot
In this naive form, this approach is no better than the linked-list approach, because the tree it creates can be highly unbalanced; however, it can be enhanced in two ways.
The first way, called union by rank, is to always attach the smaller tree to the root of the larger tree, rather than vice versa. Since it is the depth of the tree that affects the running time, the tree with smaller depth gets added under the root of the deeper tree, which only increases the depth if the depths were equal. In the context of this algorithm, the term rank is used instead of depth since it stops being equal to the depth if path compression (described below) is also used. One-element trees are defined to have a rank of zero, and whenever two trees of the same rank r are united, the rank of the result is r+1. Just applying this technique alone yields an amortized
Amortized analysis
In computer science, amortized analysis is a method of analyzing algorithms that considers the entire sequence of operations of the program. It allows for the establishment of a worst-case bound for the performance of an algorithm irrespective of the inputs by looking at all of the operations...
running-time of
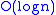per MakeSet, Union, or Find operation. Pseudocode for the improved MakeSet and Union:function MakeSet(x)
x.parent := x
x.rank := 0
function Union(x, y)
xRoot := Find(x)
yRoot := Find(y)
if xRoot yRoot
return
// x and y are not already in same set. Merge them.
if xRoot.rank < yRoot.rank
xRoot.parent := yRoot
else if xRoot.rank > yRoot.rank
yRoot.parent := xRoot
else
yRoot.parent := xRoot
xRoot.rank := xRoot.rank + 1
The second improvement, called path compression, is a way of flattening the structure of the tree whenever Find is used on it. The idea is that each node visited on the way to a root node may as well be attached directly to the root node; they all share the same representative. To effect this, as
Find recursively traverses up the tree, it changes each node's parent reference to point to the root that it found. The resulting tree is much flatter, speeding up future operations not only on these elements but on those referencing them, directly or indirectly. Here is the improved Find:function Find(x)
if x.parent x
return x
else
x.parent := Find(x.parent)
return x.parent
These two techniques complement each other; applied together, the amortized
Amortized analysis
In computer science, amortized analysis is a method of analyzing algorithms that considers the entire sequence of operations of the program. It allows for the establishment of a worst-case bound for the performance of an algorithm irrespective of the inputs by looking at all of the operations...
time per operation is only
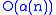, where 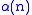is the inverse of the function 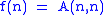, and is the extremely quickly-growing Ackermann functionAckermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
. Since
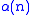is the inverse of this function, 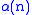is less than 5 for all remotely practical values of . Thus, the amortized running time per operation is effectively a small constant.In fact, this is asymptotically optimal
Asymptotically optimal
In computer science, an algorithm is said to be asymptotically optimal if, roughly speaking, for large inputs it performs at worst a constant factor worse than the best possible algorithm...
: Fredman
Michael Fredman
Michael Lawrence Fredman is a professor at the Computer Science Department at Rutgers University, United States. He got his Ph. D. degree from Stanford University in 1972 under the supervision of Donald Knuth. He was a member of the mathematics department at the Massachusetts Institute of...
and Saks showed in 1989 that
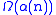words must be accessed by any disjoint-set data structure per operation on average.Applications
Disjoint-set data structures model the partitioning of a set
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
, for example to keep track of the connected components
Connected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
of an undirected graph. This model can then be used to determine whether two vertices belong to the same component, or whether adding an edge between them would result in a cycle. The Union-Find algorithm is used in high-performance implementations of Unification.
This data structure is used by the Boost Graph Library to implement its Incremental Connected Components functionality. It is also used for implementing Kruskal's algorithm
Kruskal's algorithm
Kruskal's algorithm is an algorithm in graph theory that finds a minimum spanning tree for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
to find the minimum spanning tree
Minimum spanning tree
Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees...
of a graph.
Note that the implementation as disjoint-set forests doesn't allow deletion of edges—even without path compression or the rank heuristic.
History
While the ideas used in disjoint-set forests have long been familiar, Robert Tarjan
Robert Tarjan
Robert Endre Tarjan is a renowned American computer scientist. He is the discoverer of several important graph algorithms, including Tarjan's off-line least common ancestors algorithm, and co-inventor of both splay trees and Fibonacci heaps. Tarjan is currently the James S...
was the first to prove the upper bound (and a restricted version of the lower bound) in terms of the inverse Ackermann function
Ackermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
, in 1975.
Until this time the best bound on the time per operation, proven by Hopcroft
John Hopcroft
John Edward Hopcroft is an American theoretical computer scientist. His textbooks on theory of computation and data structures are regarded as standards in their fields. He is the IBM Professor of Engineering and Applied Mathematics in Computer Science at Cornell University.He received his...
and Ullman
Jeffrey Ullman
Jeffrey David Ullman is a renowned computer scientist. His textbooks on compilers , theory of computation , data structures, and databases are regarded as standards in their fields.-Early life & Career:Ullman received a Bachelor of Science degree in Engineering...
,
was O(log* n), the iterated logarithm
Iterated logarithm
In computer science, the iterated logarithm of n, written n , is the number of times the logarithm function must be iteratively applied before the result is less than or equal to 1...
of n, another slowly-growing function (but not quite as slow as the inverse Ackermann function).
Tarjan and Van Leeuwen
Jan van Leeuwen
Jan van Leeuwen is a Dutch computer scientist, a professor at the Department of Information and Computing Sciences at the Utrecht University....
also developed one-pass Find algorithms that are more efficient in practice while retaining the same worst-case complexity.
In 2007, Sylvain Conchon and Jean-Christophe Filliâtre developed a persistent
Persistent data structure
In computing, a persistent data structure is a data structure which always preserves the previous version of itself when it is modified; such data structures are effectively immutable, as their operations do not update the structure in-place, but instead always yield a new updated structure...
version of the disjoint-set forest data structure, allowing previous versions of the structure to be efficiently retained, and formalized its correctness using the proof assistant Coq
Coq
In computer science, Coq is an interactive theorem prover. It allows the expression of mathematical assertions, mechanically checks proofs of these assertions, helps to find formal proofs, and extracts a certified program from the constructive proof of its formal specification...
.
See also
- Partition refinementPartition refinementIn the design of algorithms, partition refinement is a technique for representing a partition of a set as a data structure that allows the partition to be refined by splitting its sets into a larger number of smaller sets. In that sense it is dual to the union-find data structure, which also...
, a different data structure for maintaining disjoint sets, with updates that split sets apart rather than merging them together
External links
Partition refinement
In the design of algorithms, partition refinement is a technique for representing a partition of a set as a data structure that allows the partition to be refined by splitting its sets into a larger number of smaller sets. In that sense it is dual to the union-find data structure, which also...
, a different data structure for maintaining disjoint sets, with updates that split sets apart rather than merging them together
- C++ implementation, part of the Boost C++ libraries
- A Java implementation with an application to color image segmentation, Statistical Region Merging (SRM), IEEE Trans. Pattern Anal. Mach. Intell. 26(11): 1452-1458 (2004)
- Java applet: A Graphical Union-Find Implementation, by Rory L. P. McGuire
- Wait-free Parallel Algorithms for the Union-Find Problem, a 1994 paper by Richard J. Anderson and Heather Woll describing a parallelized version of Union-Find that never needs to block
- Python implementation